A History of Mathematical Notations/Volume 1/Egyptians
EGYPTIANS
16. The Egyptian number system is based on the scale of 10, although traces of other systems, based on the scales of 5, 12, 20, and 60, are believed to have been discovered.[1] There are three forms of Egyptian numerals: the hieroglyphic, hieratic, and demotic. Of these the hieroglyphic has been traced back: to about 3300 B.C.;[2] it is found mainly on monuments of stone, wood, or metal. Out of the hieroglyphic sprang a more cursive writing known to us as hieratic. In the beginning the hieratic was simply the hieroglyphic in the rounded forms resulting from the rapid manipulation of a reed-pen as contrasted with the angular and precise shapes arising from the use of the chisel. About the eighth century B.C. the demotic evolved as a more abbreviated form of cursive writing. It was used since that time down to the beginning of the Christian Era. The important mathematical documents of ancient Egypt were written on papyrus and made use of the hieratic numerals.[3]
17. The hieroglyphic symbols were 𓏤 for 1, 𓎆 for 10, 𓍢 for 100, 𓆼 for 1,000, 𓂭 for 10,000, 𓅨 for 100,000, 𓁨 for 1,000,000, 𓍶 for 10,000,000. The symbol for 1 represents a vertical staff; that for 1,000 a lotus plant; that for 10,000 a pointing finger; that for 100,000 a burbot; that for 1,000,000 a man in astonishment, or, as more recent Egyptologists claim, the picture of the cosmic deity Hh.[4] The symbols for 1 and 10 are sometimes found in a horizontal position.

Fig. 5.—Egyptian numerals. Hieroglyphic, hieratic, and demotic numeral symbols. (This table, was compiled by Kurt Sethe.)
18. We reproduce in Figures 5 and 6 two tables prepared by Kurt Sethe. They show the most common of the great variety of forms which are found in the expositions given by Müller, Griffith, and Brugsch.
Observe that the old hieratic symbol for ¼ was the cross 𓏴, signifying perhaps a part obtainable from two sections of a body through the center.
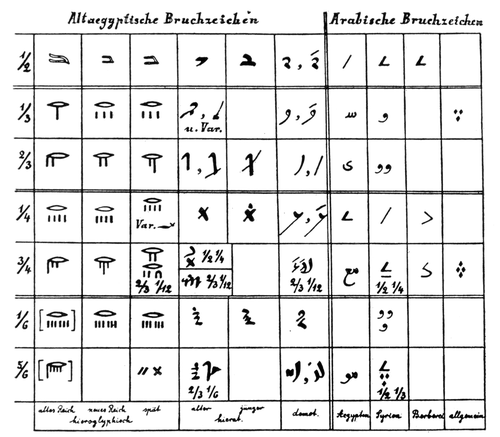
Fig. 6.—Egyptian symbolism for simple fractions. (Compiled by Kurt Sethe)
19. In writing numbers, the Egyptians used the principles of addition and multiplication. In applying the additive principle, not more than four symbols of the same kind were placed in any one group. Thus, 4 was written in hieroglyphs 𓏽; 5 was not written 𓏺𓏺𓏺𓏺𓏺, but either 𓏼 𓏻 or 𓏾. There is here recognized the same need which caused the Romans to write, V after IIII, L=50 after XXXX=40, D=500 after CCCC=400. In case of two unequal groups, the Egyptians always wrote the larger group before, or above the smaller group; thus, seven was written 𓐀.
20. In the older hieroglyphs 2,000 or 3,000 was represented by two or three lotus plants grown in one bush, For example, 2,000 was (Hieroglyphic characters); correspondingly, 7,000 was designated by (Hieroglyphic characters). The later hieroglyphs simply place two lotus plants together, to represent 2,000, without the appearance of springing from one and the same bush.
21. The multiplicative principle is not so old as the additive; it came into use about 1600–2000 b.c. In the oldest example hitherto known,[5] the symbols for 120, placed before a lotus plant, signify 120,000. A smaller number written before or below or above a symbol representing a larger unit designated multiplication of the larger by the smaller. Müller cites a case where 2,800,000 is represented by one burbot, with characters placed beneath it which stand for 28.
22. In hieroglyphic writing, unit fractions were indicated by placing the symbol 𓂋 over the number representing the denominator. Exceptions to this are the modes of writing the fractions ½, and ⅔; the old hieroglyph for ½ was 𓐞, the later was 𓐛; of the slightly varying hieroglyphic forms for ⅔, (Hieroglyphic characters) was quite common.[6]
23. We reproduce an algebraic example in hieratic symbols, as it occurs in the most important mathematical document of antiquity known at the present time—the Rhind papyrus. The scribe, Ahmes, who copied this papyrus from an older document, used black and red ink, the red in the titles of the individual problems and in writing auxiliary numbers appearing in the computations. The example which, in the Eisenlohr edition of this papyrus, is numbered 34, is hereby shown.[7] Hieratic writing was from right to left. To facilitate the study of the problem, we write our translation from right to left and in the same relative positions of its parts as in the papyrus, except that numbers are written in the order familiar to us; i.e., 37 is written in our translation 37, and not 73 as in the papyrus. Ahmes writes unit fractions by placing a dot over the denominator, except in case of ½, ⅓, ⅔, ¼, each of which had its own symbol. Some of the numeral symbols in Ahmes deviate somewhat from the forms given in the two preceding tables; other symbols are not given in those tables. For the reading of the example in question we give here the following symbols:
| Four | (symbol characters) | One-fourth | (symbol characters) | |
| Five | (symbol characters) | Heap | (symbol characters) | See Fig. 7 |
| Seven | (symbol characters) | The whole | (symbol characters) | See Fig. 7 |
| One-half | (symbol characters) | It gives | (symbol characters) | See Fig. 7 |

Fig. 7.—An algebraic equation and its solution in the Ahmes papyrus, 1700 B.C., or, according to recent authorities, 1550 B.C. (Problem 34, Plate XIII in Eisenlohr; p. 70 in Peet; in chancellor Chace’s forthcoming edition, p. 76, as R. C. Archibald informs the writer.)
Translation (reading from right to left):
“10 gives it, whole its, ¼ its, ½ its, Heap No.34 ½ 1⁄28¼ ¼½1 1 1⁄14½ ½3.. 1⁄14⅐½5 is heap the together 7 4 ¼ ⅐ Proof the of Beginning 1⁄14⅐½5 1⁄281⁄14¼½2 ½ ⅛¼ Remainder ⅛½9 together 1⁄561⁄28⅛¼1 ¼ 14 gives ¼ 1⁄561⁄281⁄281⁄141⁄14⅐ 21 Together .7 gives ⅛ 1 2 2 4 4 8”
24. Explanation:
The algebraic equations is x2+
x4+x=10
The solution answers the question, By what must (1 ½ ¼) be multiplied to yield the product 10? The four lines 2–5 contain on the right the following computation:
Twice (1 ½ ¼) yields 3½. Four times (1 ½ ¼) yields 7. One-seventh of (1 ½ ¼) is ¼.
| A table should appear at this position in the text. See Help:Table for formatting instructions. |
[Continued on facing page]
[i,ei, taking (1 12 1) once, then fourtimes, togetherwith 10f it,yields only 9; there is lacking 1. The remaining computation is on the four lines 275, on the left. Since Eof (1 5 1,) yields (‘7 1‘, 2‘“) or 9‘, 0r]
(3 2‘3) 0f (1 -‘2 3% yields 32 And the double of this, namely, (g,‘,) of (1 12 1) yields 1, Adding together 1, 4, # and (7,1;71‘4), we Obtain Heap=5ug
% 1‘4 or 5‘13, the answer.
Proof.—5½⅐1⁄14 is multiplied by (1½¼) and the partial products are added. In the first line of the proof we have 5½⅐1⁄14, in the second line half of it, in the third line one-fourth of it. Adding at first only the integers of the three partial products and the simpler fractions ½, ½, ¼, ¼, ⅛, the partial sum is 9½⅛. This is ¼⅛ short of 10. In the fourth line of the proof (l. 9) the scribe writes the remaining fractions and, reducing them to the common denominator 56, he writes (in red color) in the last line the numerators 8, 4, 4, 2, 2, 1 of the reduced fractions. Their sum is 21. But 2156=14+756=14 18, which is the exact amount needed to make the total product 10.
A pair of legs symbolizing addition and subtraction, as found in impaired form in the Ahmes papyrus, are explained in §200.
| A table should appear at this position in the text. See Help:Table for formatting instructions. |
Fig. 8.—Hieroglyphic, hieratic and Coptic numerals. (Taken from A. P. Pihan, Exposé des signes de numération [Paris, 1860], p.26, 27.
25. The Egyptian Coptic numerals are shown in Figure 8. They are of comparatively recent date. The hieroglyphic and hieratic are the oldest Egyptian writing; the demotic appeared later. The Coptic writing is derived from the Greek and deinotic writing, and was used by Christians in Egypt after the third century. The Coptic numeral symbols were adopted by the Mohammedans in Egypt after their conquest of that country.
26. At the present time two examples of the old Egyptian solution of problems involving what we now term “quadratic equations”[8] are known. For square root the symbol 𓊋 has been used in the modern hieroglyphic transcription, as the interpretation of writing in the two papyri; for quotient was used the symbol (symbol characters).
- ↑ Kurt Sethe, Von Zahlen und Zahlworten bei den alten Ägyptern (Strassburg, 1916), p. 24–29.
- ↑ J. E. Quibell and F. W. Green, Hierakonopolis (London, 1900–1902), Part I, Plate 26B, who describe the victory monument of King Ncr-mr; the number of prisoners taken is given as 120,000, while 400,000 head of cattle and 1,422,000 goats were captured.
- ↑ The evolution of the hieratic writing from the hieroglyphic is explained in G. Möller, Hieratische Paläographie, Vol. I, Nos 614 ff. The demotic writing is explained by F. L. Griffith, Catalogue of the Demotic Papyri in the John Rylands Library (Manchester, 1909), Vol. III, p. 415 ff., and by H. Brugsch, Grammaire démotique, §§ 131 ff.
- ↑ Sethe, op. cit., p. 11, 12.
- ↑ Ibid., p. 8.
- ↑ Ibid., p. 92–97, gives detailed information on the forms representing ⅔. The Egyptian procedure for decomposing a quotient into unit fractions is explained by V. V. Bobynin in Abh. Gesch. Math., Vol. IX (1899), p 3.
- ↑ Ein mathematisches Handbuch der alten Ägypter (Papyrus Rhind des British Museum) übersetzt und erklärt (Leipzig, 1877; 2d ed., 1891). The explanation of Problem 34 is given on p. 55, the translation on p. 213, the facsimile reproduction on Plate XIII of the first edition. The second edition was brought out without the plates. A more recent edition of the Ahmes papyrus is due to T. Eric Peet and appears under the title The Rhind Mathematical Papyrus, British Museum, Nos. 10057 and 10058, Introduction, Transcription, and Commentary (London, 1923).
- ↑ See H. Schack-Schackenburg, “Der Berliner Papyrus 6619.” Zeitschrift für ägyptische Sprache und Altertumskunde, Vol. XXXVIII (1900), p. 136, 138, and Vol. XL (1902), p. 65–66.