| Pascal’s Theorem.—If a hexagon be inscribed in a curve of the second order, then the intersections of opposite sides are three points in a line. | Brianchon’s Theorem.—If a hexagon be circumscribed about a curve of the second class, then the lines joining opposite vertices are three lines meeting in a point. |
These celebrated theorems, which are known by the names of their discoverers, are perhaps the most fruitful in the whole theory of conics. Before we go over to their applications we have to show that we obtain the same curve if we take, instead of S1, S2, any two other points on the curve as centres of projective pencils.
§ 52. We know that the curve depends only upon the correspondence between the pencils S1 and S2, and not upon the special construction used for finding new points on the curve. The point A (fig. 16 or 18), through which the two auxiliary rows u1, u2 were drawn, may therefore be changed to any other point on the curve. Let us now suppose the curve drawn, and keep the points S1, S2, K, L and D, and hence also the point S fixed, whilst we move A along the curve. Then the line AL will describe a pencil about L as centre, and the point D1 a row on S1D perspective to the pencil L. At the same time AK describes a pencil about K and D2 a row perspective to it on S2D. But by Pascal’s theorem D1 and D2 will always lie in a line with S, so that the rows described by D1 and D2 are perspective. It follows that the pencils K and L will themselves be projective, corresponding rays meeting on the curve. This proves that we get the same curve whatever pair of the five given points we take as centres of projective pencils. Hence—
| Only one curve of the second order can be drawn which passes through five given points. | Only one curve of the second class can be drawn which touches five given lines. |
We have seen that if on a curve of the second order two points coincide at A, the line joining them becomes the tangent at A. If, therefore, a point on the curve and its tangent are given, this will be equivalent to having given two points on the curve. Similarly, if on the curve of second class a tangent and its point of contact are given, this will be equivalent to two given tangents.
We may therefore extend the last theorem:
| Only one curve of the second order can be drawn, of which four points and the tangent at one of them, or three points and the tangents at two of them, are given. | Only one curve of the second class can be drawn, of which four tangents and the point of contact at one of them, or three tangents and the points of contact at two of them, are given. |
§ 53. At the same time it has been proved:
| If all points on a curve of the second order be joined to any two of them, then the two pencils thus formed are projective, those rays being corresponding which meet on the curve. Hence— | All tangents to a curve of second class are cut by any two of them in projective rows, those being corresponding points which lie on the same tangent. Hence— |
| The cross-ratio of four rays joining a point S on a curve of second order to four fixed points A, B, C, D in the curve is independent of the position of S, and is called the cross-ratio of the four points A, B, C, D. | The cross-ratio of the four points in which any tangent u is cut by four fixed tangents a, b, c, d is independent of the position of u, and is called the cross-ratio of the four tangents a, b, c, d. |
| If this cross-ratio equals −1 the four points are said to be four harmonic points. | If this cross-ratio equals −1 the four tangents are said to be four harmonic tangents. |
We have seen that a curve of second order, as generated by projective pencils, has at the centre of each pencil one tangent; and further, that any point on the curve may be taken as centre of such pencil. Hence—
| A curve of second order has at every point one tangent. | A curve of second class has on every tangent a point of contact. |
§ 54. We return to Pascal’s and Brianchon’s theorems and their applications, and shall, as before, state the results both for curves of the second order and curves of the second class, but prove them only for the former.
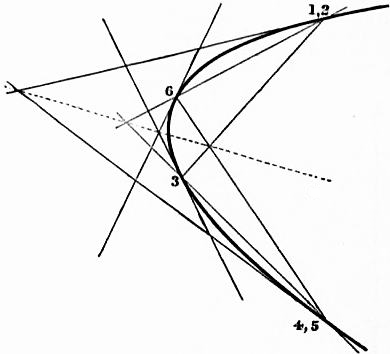
Pascal’s theorem may be used when five points are given to find more points on the curve, viz. it enables us to find the point where any line through one of the given points cuts the curve again. It is convenient, in making use of Pascal’s theorem, to number the points, to indicate the order in which they are to be taken in forming a hexagon, which, by the way, may be done in 60 different ways. It will be seen that 1 2 (leaving out 3) 4 5 are opposite sides, so are 2 3 and (leaving out 4) 5 6, and also 3 4 and (leaving out 5) 6 1.
If the points 1 2 3 4 5 are given, and we want a 6th point on a line drawn through 1, we know all the sides of the hexagon with the exception of 5 6, and this is found by Pascal’s theorem.
If this line should happen to pass through 1, then 6 and 1 coincide, or the line 6 1 is the tangent at 1. And always if two consecutive vertices of the hexagon approach nearer and nearer, then the side joining them will ultimately become a tangent.
We may therefore consider a pentagon inscribed in a curve of second order and the tangent at one of its vertices as a hexagon, and thus get the theorem:
| Every pentagon inscribed in a curve of second order has the property that the intersections of two pairs of non-consecutive sides lie in a line with the point where the fifth side cuts the tangent at the opposite vertex. | Every pentagon circumscribed about a curve of the second class has the property that the lines which join two pairs of non-consecutive vertices meet on that line which joins the fifth vertex to the point of contact of the opposite side. |
This enables us also to solve the following problems.
| Given five points on a curve of second order to construct the tangent at any one of them. | Given five tangents to a curve of second class to construct the point of contact of any one of them. |
 |
| Fig. 19. |
If two pairs of adjacent vertices coincide, the hexagon becomes a quadrilateral, with tangents at two vertices. These we take to be opposite, and get the following theorems:
| If a quadrilateral be inscribed in a curve of second order, the intersections of opposite sides, and also the intersections of the tangents at opposite vertices, lie in a line (fig. 19). | If a quadrilateral be circumscribed about a curve of second class, the lines joining opposite vertices, and also the lines joining points of contact of opposite sides, meet in a point. |
 |
| Fig. 20. |
If we consider the hexagon made up of a triangle and the tangents at its vertices, we get—
| If a triangle is inscribed in a curve of the second order, the points in which the sides are cut by the tangents at the opposite vertices meet in a point. | If a triangle be circumscribed about a curve of second class, the lines which join the vertices to the points of contact of the opposite sides meet in a point (fig. 20). |
§ 55. Of these theorems, those about the quadrilateral give rise to a number of others. Four points A, B, C, D may in three different ways be formed into a quadrilateral, for we may take them in the order ABCD, or ACBD, or ACDB, so that either of the points B, C, D may be taken as the vertex opposite to A. Accordingly we may apply the theorem in three different ways.
Let A, B, C, D be four points on a curve of second order (fig. 21), and let us take them as forming a quadrilateral by taking the points in the order ABCD, so that A, C and also B, D are pairs of opposite vertices. Then P, Q will be the points where opposite sides meet,
