While in the foregoing examples special stress was put on the relative identity of mechanical principles in engineering and nature, it will, in the next place, be interesting to show that in many cases the laws of rational construction and design are at a glance geometrically apparent.
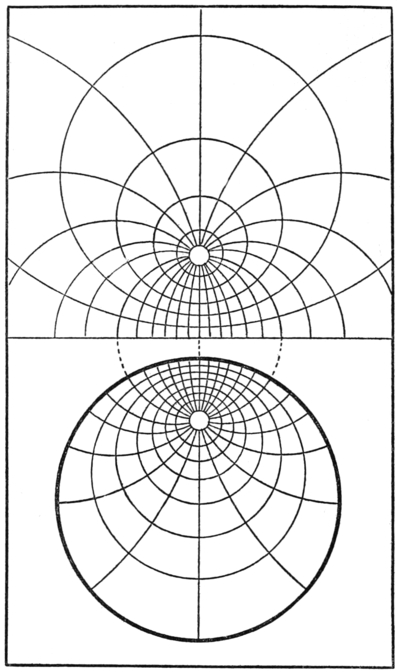
If we think of the cross-section of a tree, further growth must necessarily occur in directions normal to the surface of the last year ring. This causes the year-rings and pith-rays to form a system of orthogonal trajectories. In Fig. 4 such a system, consisting of two conjugate pencils of circles, is shown, and is caused by a rate of growth greater in one direction than another.
The inner yellow portion of a daisy (Chrysanthemum leucanthemum) exhibits a beautiful geometrical arrangement of its elements. By the mathematical principle of conformal transformations it can