BP, and from the point P draw the right lines PT, PR meeting BD, CD in T and R, and making the angle BPT equal to the given angle BNM and the angle CPR equal to the given angle CNM, Wherefore ſince (by ſuppoſition) the angles MBD, NBP are equal, as alſo the angles MCD, NCP; take away the angles NBD and NCD that are common, and there will remain the angles NBM and PBT, NCM and PCR equal; and therefore the triangleſs NCM, PBT are ſimilar, as alſo the triangles NCM, PCR. Wherefore PT is to NM as PB to NB; and PR to NM, as PC to NC. But the points B, C, N, P are immovable: Wherefore PT and PR have a given ratio to NM, and conſequently a given ratio between themſelves; and therefore, (by lem. 20.) the point D wherein the moveable right lines BT and CR perpetually concur, will be placed in a conic ſection paſſing through the points B, C, P. Q. E. D.
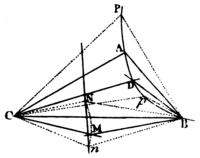
And vice verſa, if the moveable point D (Pl. 9. Fig. 4.) lies in a conic ſection paſſing through the given points B, C, A; and the angle DBM is always equal to the given angle ABC, and the angle DCM always equal to the given angle ACB, and when the point D falls ſucceſſively on any two immovable point p, P, of the conic ſection, the moveable point M falls ſucceſſively on two immovable points n, N: through theſe points n, M draw the right line nM, this line nN will be the perpetual locus of that moveable point M. For if poſſible, let the point M be placed in any curve line. Therefore the point D will be placed in a conic ſection paſſing through the five points B, C, A, p, P, when the point M is perpetually placed in a curve line. But from what was demonſtrated before, the point D
