CHAPTER I.
GENERAL OUTLINES.
§ 1.
Nature of the Machine-Problem.
While in appearance a machine differs greatly from any of the force- or motion-distributors of nature, yet for the theoretical or pure mechanician no such difference exists,—or rather it completely disappears on analysis, so that to him the problems of machinery fall into the same class as those of the mechanical phenomena of nature. He sees in both forces and motions existing, and subject to the same great laws which, developed in their most general form, govern and must govern every single case. In pure Mechanics machines are now treated only as illustrations; they no longer receive their complete development as they did when many of their problems were still new and strange, and apparently stood opposed to those of Mechanics. This present subdivision is quite correct, so far as the question is one of scientific comprehension only. As, however, the actual machinery itself, deriving its existence from various sources, and having its own characteristic features and methods of classification and treatment, forms a quite distinct and special subject, a separation of its scientific mechanical problems from those of Mechanics in general is possible, and indeed has already been made.
It must be admitted, too, that the sense of the reality of this separation has been felt not only by Engineers or others actually engaged in machine design, but also by those theoretical writers who have had any practical knowledge of machinery, in spite of the increasing tendency in the treatment of mechanical science to thin away machine-problems into those of pure mechanics.
There are good reasons for this feeling. Such a treatment of machine-problems is first of all greatly to be deprecated because it would place the scientific part of machine-construction upon a base too indefinite and widely extended. The fundamental notions of force and motion themselves are subject to uncertain interpretation. In the attempt to define ideas standing on the boundary line between Physics and Metaphysics an uncertainty which demands the closest mathematical and philosophical investigation makes itself felt. This uncertainty or indistinctness, by holding open a perspective of ideas entirely beyond all purpose of the study concerned, exercises a disturbing influence on it. It affects every definition, every explanation intended to be exhaustive; it compels the teacher who desires to express himself with scientific accuracy either to use generalisations of which he feels the unpractical nature, or to employ illogical limitations such as "common practice," "usual arrangements," and so on. He who knows laws only is fain to content himself with rules where he would far sooner employ strict scientific methods. Not every generalisation, that is to say, is practical, nor from a certain point of view indeed, even correct. This point of view is that from which Geometry separates itself from Mathematics in general, Descriptive Geometry from Geometry in general, still more from which Kosmical Physics, Hydraulics, Aerostatics, branch away from Natural Philosophy,—in other words, the point of view from which special sciences are seen to separate themselves from the more general sciences to which they are subordinate.
Such a separation becomes at once possible and advisable if any complete circle of ideas lie at the base of the region separated. In the case of machine-problems their separation from those of general Mechanics can be demonstrated. A distinct line of demarcation, although in certain examples less distinct than in others, shows itself between them. To find the real nature of this difference let us endeavour to look at the whole question from outside, examining, without regard to any existing machine-theories, one and the same motion as it appears in Nature and in the Machine.
Let us take the case of a circular motion, which shall be supposed to occur first as the motion of a satellite about its planet; and then as the revolution of a wheel.

Fig. 2.
Suppose that from any cause the satellite (Fig. 2) so move about the planet that its centre describes a circle about the centre of in a plane passing through that point. So long as the conditions remain unaltered the motion continues the same. So soon however as any external disturbing force (shown here perpendicular to the plane of motion), begins to act upon one side of , alters its path. If this is to be prevented, another external force , equal and opposite to , must be brought simultaneously into action. If be a pound, must be also a pound; if increase to a ton, must increase to a ton also; the absolute value of does not further enter into the question, which is one solely of the equilibrium of the external disturbing forces acting upon . The existence of such an equilibrium in nature would presuppose the existence always of equally divided causes of force; it probably does not once occur in the case of celestial bodies. We are however at liberty to assume its possibility in order to simplify the matter.
In the machine the case is quite different, and much more simple. In order that points of the wheel , Fig. 3, may move in circles, let it be fixed upon a rigid shaft of which the ends at and are turned down and fitted in holes in fixed and rigid supports , the whole system having a common geometrical axis. If now the wheel be set in motion by some suitable handle, every point in it lying beyond its geometrical axis describes a circle about some point in that axis. If any disturbing force act sideways upon the wheel, then (if we suppose the material of the wheel, shaft, and bearings to be completely rigid) no alteration of the circular motion occurs; and this is true equally whether be great or small, continuous or intermittent, constant or changing in direction. There is nevertheless continuous equilibrium here, but in another way than before. So soon as the force begins to act it calls forth in the interior of the wheel, the shaft and the supports, internal molecular forces, opposite in direction and exactly equal to it. The action of the forces therefore, considered by themselves, is here exactly the same as, or exactly corresponding to, their action in the case of the satellite. There exists however the difference that there all external forces are independent of each other, while here the action of an external force becomes at once the cause of the opposite action of a molecular force.
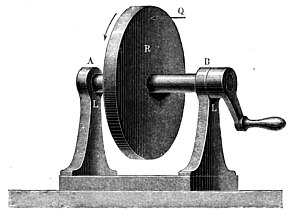
Fig. 3
In actual machines we do not employ absolutely rigid material, for no such material exists; we use however only those materials which when of suitable dimensions alter their form under the action of external forces very little, so little that the corresponding variations from the original form may be neglected, The choice of suitable dimensions and forms is the work of the machine designer. If we disregard the very small variations of form which actually occur, it appears that the solution of the problem by the machine exists, and also that it differs essentially from that occurring in nature:
Whilst in the first system, which we may call kosmical, the external measurable mechanical forces are opposed by similar external forces, in the second, the machine system, there are opposed to all external forces others concealed in the interior of the bodies forming the system, and appearing there,—and acting in exactly the required manner,—in consequence of the action of the external forces. One might apply to these forces,—with a very small alteration which I hope the reader will permit,—Schiller's riddle about the spark:—
"Sleeping, yet ready for the expected foe,
I lie concealed within my iron walls;
He comes, he feels my iron weapon's blow,
We fight; I sleep again,—for soon he falls."
The force is challenged, and immediately it appears;—the external challenging force ceases, and immediately its opponent, which has so energetically defended the form of its dwelling, also disappears. Nothing is to be seen of the inner force so long as it is not awakened by an outer one. It is as it were concealed in the interior of the body. We shall not be carrying the analogy with Thermal Physics too far if we call these molecular forces, which in their hiding-places guard the stability of the material world, latent forces, as opposed to the directly measurable sensible forces which externally influence bodies through gravitation and other causes. The difference between the two systems is therefore that sensible forces are in the one case opposed by other and independent sensible forces, and in the other case by dependent latent forces.
We have considered both systems in a form of special simplicity which, it may be thought, does not permit sufficiently general deductions to be made. Then let us suppose the kosmical system to be enlarged into a solar system with sun, planets, and satellites moving in their circular or elliptic orbits, and let us add to our wheel other wheels and shafts connected with the first as spur-gearing or in any other way, so that rotation occurs throughout the whole system, and a machine suitable for any particular purpose is formed. We shall then note that in the kosmical system the mutual motions of the bodies, both as to their paths and their velocities, are entirely dependent on the influence of sensible forces, while in the machine system the paths of motion are absolutely determined, and at the same time no point can alter its velocity without the velocities of all other points being correspondingly altered; that in the latter case, therefore, disturbing sensible forces are without influence,—they are everywhere balanced by the latent forces. Not less is it these last which carry the moving forces from body to body. The difference we found above, then, is general, so far as it relates to the nature of the forces coming into action, and is in no way limited to the simple case supposed.
Both the cases chosen as illustrations are extreme,—in general the kosmical and machine systems do not differ so widely, but approach each other mutually more or less. The plant, for instance, so far resembles a machine system that the motion of its sap takes place in tolerably rigid channels or tubes, and in definite prescribed directions. The correspondence is not, however, exact, for the leaf-stalks, twigs and boughs undergo alterations of form both small and great from kosmical forces. The nearest approach to our machine system in the vegetable kingdom is perhaps the circulation of the sap in the tissue of a firm, strong tree-stem, for here only are the alterations of form small enough to be neglected. In a few existing machines also actions occur which must be classed as kosmical, as for instance the motion of the water in the ancient water-wheels (Straube-räder) used sometimes in mountainous districts to drive saw-mills, upon which the stream dashes almost like a waterfall. Thus the two systems are not divided by a hair-line, but still their differences are always notable, and become the more distinct the more decidedly each belongs to its own class. The more perfectly the water-wheel is made, the more completely do the freely-playing streams of water disappear; the rude wheel becomes the smooth and quietly running turbine, where the foaming and splashing of the water is reduced to the smallest limits. From the huge swinging lever, by the help of which the Walloon brickmaker or the Hindoo builder lowered his empty bucket into the brook and raised it again full, has grown the beam-engine, with its quiet and regularly working pumps. The kosmical freedom of natural forces is brought in the machine under order and law, which no ordinary external force can shake. On the other hand, latent forces also act with those of nature, as in the waterfall, hurling the rebounding streams of water upwards from the rocky channel; or as in the meteoric stone, diverting it from its original path by atmospheric resistance. The balancing of sensible by latent forces is therefore not solely a distinctive mark of the machine but we have in it a principal characteristic of the machine-like or machinal as distinguished from the kosmical, and it must be kept distinctly in view in endeavouring to understand the exact idea conveyed by the word machine.
The prevention of disturbing motions by latent forces is then a principle in the machine. Its application is connected with various objects. When a machine is constructed it is meant to be an arrangement for carrying on some definite mechanical work—it may be the moving of some body, or the alteration of its form, or both together. For such a purpose we require that so soon as motion is caused by any effort in any part of the machine that motion shall be of an absolutely defined nature. Thus our wheel in Fig. 3 might be used for lifting weights if we made the disc a drum and passed a cord over it,—or it might serve as a grindstone if the disc were made of suitable material, and so on. Every motion then which varies from the one intended will be a disturbing motion, and we therefore give beforehand to the parts which bear the latent forces—the bodies, that is, of which the machine is constructed,—such arrangement, form and rigidity that they permit each moving part to have one motion only, the required one. This having been done, so soon as the external natural forces which it is intended to employ are allowed to act, the desired motion occurs. Our procedure is therefore twofold; negative first—the exclusion of the possibility of any other than the wished-for motion; and then positive—the introduction of motion. The result is that the natural force when applied accomplishes the required mechanical work.
A machine may be perfect, or may contain more or fewer imperfections; it approaches perfection just in proportion as it corresponds to what we have recognised as its special object,—the special end for which it has been constructed. After the insight we have now obtained into its nature it is possible for us to frame a definition of the machine. It is as follows:—
A machine is a combination of resistant bodies so arranged that by their means the mechanical forces of nature can be compelled to do work accompanied by certain determinate motions.7
This shows within what distinct limits machine-problems lie, and that they allow themselves to be readily separated from the general problems of Mechanics, as we have already maintained.
While the science of Mechanics examines motion caused in the most general cases by the action of mechanical forces, Machine-mechanics occupies itself with certain special cases only, with motions produced by a limited circle of means. It draws its first laws from the same fountain as Mechanics, to which, as the more comprehensive science, it is subordinate. But the region which it specially concerns can be separated from the science as a whole, and its function is to create systematic order within this separate region, and to investigate the laws specially belonging to it. Here is work enough, challenging some one to undertake it. It is greatly to be wished that those who are familiar with machine-design should not leave these investigations entirely to others, as has of late years often been the case with us, and still more in France. It is this that has caused what I have already alluded to as the volatilisation, the thinning away, of the problem,—a method of treatment from which practical mechanists, upon whom the machine depends for its further development, and for whose benefit specially the investigations have been undertaken, turn away dissatisfied. They have the right to demand, within certain limits, complete concentration upon their special problems, and will not allow the question to be carried off into another region, where the solid ground seems to them to disappear without any counterbalancing advantages being gained.
§ 2.
The Science of Machines.
The scientific carrying-out in practice of the requirements covered by our definition of the machine has caused the rise of an extended apparatus of sciences in connection with the progressing development of Polytechnic instruction. From the foundation sciences of Mathematics and Physics three or four other sciences specially concerning the machine have separated themselves. Their common object is the elucidation of the causal-connection of machine phenomena. Together they have been happily enough called Practical Mechanics. I speak of them here as sciences without pretending to insist on their absolute right to the title; they may be called sciences of the second or third order, or by their usual names; they employ scientific methods, and treat by their means special regions of investigation; within these they have reached by degrees an independence which has made necessary their separation, from the more general sciences.
First comes the study of machines in general, looked at in connection with the work they have to do. This is known in Germany under a number of somewhat vague titles, as general or descriptive, special and theoretical "Maschinenlehre." In its general form it deals, descriptively, with the whole of existing machines,—it teaches what machines exist and how they are constituted, and thus affords us a glance at their manner of growth. It proceeds teleologically in the fullest sense of the word, seeking always to refer everything to the special object for which the machine was constructed. Its methods of classification are made as general as possible. At present a complete descriptive, or really general treatment of machinery in this way, is hardly possible on account of the enormous number of existing machines. To be really general only classes and types can be treated of. Quietly adapting itself to the every-day wants of the learner the study thus becomes specialised,—single classes are taken up and treated singly in detail. Along with the construction of each special machine its theory is also, for the most part, considered, that is, the nature of the sensible forces which come into action and the motions to which they give rise are examined, and deductions are drawn in regard to the most suitable way for turning these forces to account. This method of treatment is therefore based also on existing machines, but differs from the former in not only describing their arrangement and purpose, but in examining also how they can best be arranged in order to carry out the given purpose. In Germany at present it is for the most part rightly grasped and comprehended, the machine itself being taken as both the end and the beginning of the problem. The French, however, have not always freed themselves from the idea that the machine occurs merely as an illustration—an example—in Applied Mechanics; if this idea were right, however, it is clear that all other applications of Mechanics should be treated in the same way. If,—coming somewhat nearer to the heart of the matter,—the applications of mechanics "in machinery" be classed by themselves, as is done by Poncelet,—still the principle is not carried sufficiently far, for under this title all machines of every kind must be treated, which, however, has not been the case. Redtenbacher first removed this stigma of indistinctness from the matter, and thereby laid the foundation of the freshness and power which the German system of machine-instruction shows as contrasted with the French. Redtenbacher's most lasting services, which have not always been, understood by his successors, lie in this direction,—in the separation of the questions connected with machinery into separate sciences or branches of science. It was on this ground that his influence was, I may say, so electric; and brought to him so quickly in his time the engineering students of Germany.
The existing treatment of the theory of machines (theoretische Maschinenlehre) confines itself principally to prime-movers,—Steam-engines, Water-wheels, Turbines, Windmills, and so on,—or in terms of our definition, it concerns itself with the nature of the various arrangements by means of which natural forces can be best applied in machinery. Yet it does also consider machines in general (other than prime-movers), and obviously these all belong to its province. To the general examination of the theory of these machines the name mechanical technology is often given. This is not universal, nor indeed is it correct, for mechanical technology must include all mechanical processes of manufacture, and in a multitude of cases machines are not employed in these. It possesses therefore a domain of its own, and must be treated in its own proper way. From its own point of view it also examines the machine, but in a way entirely differing from that in which it is examined for its own sake in the studies of which we are speaking. While therefore it can easily be understood how both studies should set up claims to the same object of instruction, it is on that very account important that they should not be confused with each other.
The special part of technology here coming into question,—or what may be called the technological part of the study of special machines,—concerns itself with the action of the natural forces, through their various applications in the machine, on the bodies to be worked upon. It examines, in other words, by what special arrangement of the parts of the machine the required action can be best obtained. As a whole, therefore, the specialised study of machines (specielle Maschinenlehre) considers both the application of the natural forces to a given machine and their action in it.
The third science is that of Machine-design. It also has been freed by Redtenbacher from its incorrect treatment under Applied Mechanics, and placed by him on an independent footing. Its province is to teach how to give to the bodies constituting the machine the capacity for resisting alteration of form mentioned in our definition. In order to determine this property fully it must be considered in reference not only to sensible but also to latent forces.
The first it accepts as found by the aid of the Science just examined, in the shape for example of the steam pressure upon a piston, the water pressure in a turbine, and so on; these determine the strength of the bodies. The latter, the latent forces, carry the force-action from body to body,—e.g. from piston-rod to connecting-rod, from spur-wheel to spur-wheel, and so on; and cause therefore necessarily friction and wear. The problems of machine-design extend in both the directions thus pointed out. In solving these problems in such a way as to conform to the technological conditions of each special case, machine-design forms itself into a really technical science. Its twofold nature, as concerning itself both with sensible and with latent forces, which hitherto has been recognised in fact without being known to theory, I wish to raise into the position of a leading principle; its reality has been clearly proved from the general development of fundamental propositions.
Now, lastly, our definition covers a fourth characteristic of the machine which has not been a leading idea in either of the three studies we have considered. This is the arrangement of the means for insuring that only certain determined motions shall occur in the machine. So far certainly as the motions are conditioned by forces, and are regarded solely in connection with force-actions, they have been considered in studying the theory of machines in the way already described. But that study simply takes the motions looked at as changes of position as given. Hence another series of investigations remain, their subject being the nature of the mutual dependence of the changes of position of parts of the machine. If the problems here presenting themselves be treated separately, those of the three former studies being supposed to be solved, they form a province of investigation which can be worked in by means of Applied Mathematics and Mechanics. The systematised study of the solutions of these problems forms the science with which we have to do, Kinematics, the "Science of Pure Mechanism."[1] It is, as follows from what we have said, the study of those arrangements of the machine by which the mutual motions of its parts, considered as changes of position, are determined.
The difference between this definition of Kinematics and that which Ampère indicated rather than gave fully (see Introduction, p. 11) requires to be noticed. It is principally this, that here Kinematics is made to belong essentially not to Mechanics, as with Ampère, but to the Science of Machines, as has been done more or less, but without any distinct admission of it, by most of Ampère's followers. Its objects and methods subordinate themselves therefore to the chief laws which affect the machinal as distinguished from the kosmical, and must at the same time fit in with the methods of treatment received by the machine in the three different studies already described. So far, that is to say, Kinematics is not an absolutely isolated science, as it would be under Ampère's definition, but works in consciousness of the neighbourhood of other systems of investigation having a common object with it. On the other hand we have in our own way arrived at the same conclusion with Ampère, that Kinematics observes changes of position only. Only we do not thereby shut out the actions of forces, as Ampère does; we take the problems connected with them as solved in every case, and consider the conditions imposed by them, which is a real and important difference. The indistinctness remaining with Ampère upon this point has been the cause of the unavoidable introduction by his followers of fragments of three other studies, with which they could not dispense: thus, for example, Haton gives an abstract of the strength of materials, Laboulaye this and the study of friction also, and so on.[2] Summarising this section, we see that "Practical Mechanics" has been subdivided into—
- The study of Machinery in general.
- The special or theoretical study of Machinery.
- The study of Machine-design.
- The study of pure Mechanism.
For the understanding of the nature of machines the last-named science is evidently as important as the three first; indeed in many respects it must stand first and prepare the way for them, and on this account single sections of Kinematics are often included in all three. The union of the three last sciences is necessary that the machine may be completely understood, the first having pointed out its existence and treated it teleologically. All four interact continually; only as a whole do they furnish the practical mechanist with complete solutions to all the problems of his work.
§ 3.
General solution of the Machine-Problem.
We must now proceed to establish the general principles of kinematic procedure, in order to gain a standpoint from which to survey generally the method of solving our problem. The ideas above developed concerning the essential nature of machine-systems will serve as an introduction to this. Those parts of a machine transmitting the forces by which the moving points are caused to limit their motions in the definite and required manner must be bodies of suitable resistant capacity, the moving points themselves must belong also to similar bodies. In the machine, consequently, the moving bodies are prevented, by bodies in contact with them, from making any other than the required motions. This contact also, if the problem is to be entirely solved, must take place continually, which presupposes the possession of certain properties by the bodies in contact. In proceeding to examine these properties more closely, we shall assume in the first instance that the bodies possess complete rigidity, and shall pay no attention to their size,—in other words we take all questions belonging to what we have called the special study of machinery and the study of machine-design as solved, so that only geometrical properties remain for us to consider.
Fig. 4.
Now in order that any moving body , of given form, may remain continually in contact with a stationary one , we must give to the latter a special form. This can be found if the body be caused to take up consecutively the series of positions which it is intended to occupy relatively to , and the figure which envelopes all the positions of the outline of the body determined. If for example be a parallelopiped (Fig. 4), of which one surface remains during its motion in a plane, the figure will become a curved channel. The geometrical form thus found for is called the envelope of the moving figure . has to also the same relation as to , that is, is the envelope to , or at least those points in the figure with which comes into contact form the envelope of the body in respect to . The relation, therefore, is reciprocal.
Many such reciprocal envelopes can be actually constructed, If a moving body be surrounded by stationary ones containing its envelope in such a way that at no instant is more than one motion of the body possible, then its motion must necessarily be such as belongs to the envelopes, and is determined by their form.
We see at once that at least one other body is necessary for the envelopment of a moving form. If it be found necessary to use several—perhaps because the one first found, while actually forming an envelope, does not exclude all motions but the one required,—then these can be united with the first into one body. Thus for instance we can suppose the upper and lower half brasses of a plummer block joined together. We find, that is to say, that in all cases at least two bodies correspond in being reciprocally envelopes each of the other. A machine consists solely of bodies which thus correspond, pair-wise, reciprocally. These form the kinematic or mechanismal elements of the machine.
The shaft and the bearing, the screw and the nut, are examples of such pairs of elements. We see here that the kinematic elements of a machine are not employed singly, but always in pairs; or in other words, that the machine cannot so well be said to consist of elements as of pairs of elements. This particular manner of constitution forms a distinguishing characteristic of the machine.
Fig. 5.
Fig. 6.
If a kinematic pair of elements be given, a definite motion can be obtained by means of them if one of the two be held fast or fixed in position,—that is, be brought to rest relatively to a given portion of space chosen with reference to the motion which is to be observed. The other element is then free to be moved, but only in the one particular way allowed by the constitution of the pair. Its motion relatively to its companion element is under these conditions the same as its absolute motion in the given portion of space. Thus, for example, in the pair of elements shown in Fig. 5,—a screw and nut,—if the former be fitted with a suitable foot or its equivalent, so as to prevent its motion, then each point in the nut, if it be moved, will describe a helix of determinate magnitude. In the pair shown in Fig. 6, which consists of a solid prism enclosed by a corresponding hollow one, all points of the latter describe straight lines of equal length if it be set in motion after the former has been fixed.
Fig. 7.
A large number of motions can be obtained in this way simply by pairs of elements, as we shall have occasion further on to see more in detail, while the complete development of their properties affords the means of multiplying indefinitely the motions obtainable by single pairs. This can be done by the combination of pairs.
Fig. 8.
Let it be desired to combine two pairs of elements, and ;—this must take place so that each of the elements of one pair be combined with, that is made part of the same solid body as, one of the elements of the other pair. This, moreover, may occur so that the mutual relation of the parts is not altered, and no new motion obtained. If the element be joined to , then must be combined with ; or if be combined with , then must be joined to . We may illustrate this by an example, Fig. 7. Suppose that and be two similar pairs, and being cylinders, and prismatic slots in bars, having such a form as to prevent either sideway or endlong motion of the cylinders. Let and be so joined that their axes are parallel, and let the two slotted bars be also placed parallel to each other and joined. Then evidently, if be fixed, every point in must move parallel to the centre line of the slots, as shown by the arrow. All such points therefore describe equal straight lines. Thus the motion takes place exactly as it would if were a solid prism enclosed by a hollow one, like the pair in Fig. 8. Thus by combining two pairs we have obtained nothing but what we could have got by means of a single one. So far the experiment has led to no result.
Fig. 9.
But if we do not place and parallel to each other, but set them obliquely as shown in Fig. 9, the case is entirely altered. The centres of and no longer move in similar directions in the slots, and consequently the various points in no longer have similar paths,—the point , for example, describes a curve. The motion is thus quite different from what it was before.
Nevertheless in these two different cases, Figs. 7 and 9, the same relation obtains; in both, and form rigid bodies, or what may be considered as such,—that is to say, we have in the end one pair of elements only, by combining two pairs of bodies. With different methods of combination different results are obtained, but in every case there results only one pair.
Accordingly the reciprocal combination of the elements of two pairs gives us again a pair of elements, which may differ from either of the single pairs of which it is composed. Thus we obtain already an important result, and one having many consequences. We may now proceed to the combination of three or four pairs of elements. Suppose the pairs
to be given. Let each element of each of these be joined to one element of another pair,—then every pair keeps its own peculiarity and at the same time has another added to it. The combination may take place in a number of different ways, for example in the same order as above.
;
or in the order
,
and so on. The whole now forms a linkage returning upon itself, like an endless chain, consisting simply of single links connected together. A combination of pairs of elements in this way we shall call a chain, or more fully a kinematic chain. The body which is formed by the junction of the elements of two different pairs is then a link of the kinematic chain. Every link of the above-mentioned chain consists of two elements, so that the chain here has as many links as it contains pairs.
In the chain every two adjacent links have a definite relative motion, that namely which belongs to the pair of elements connecting them. But two links which are connected by a third do not possess definite reciprocal motions except under certain conditions. Such motions can occur only if the chain be so arranged that every alteration in the position of a link relatively to the one next to it be accompanied by an alteration in the position of every other link relatively to the first. In a kinematic chain which possesses this peculiarity, each link has only one relative motion to each other link; if, that is to say, any relative motion occur in the chain, all the links are constrained to execute determinate relative motions. Such a kinematic chain I call a constrained closed—or simply a closed—chain.
We may take as an illustration the simple chain shown in figure 10. It consists of four similar pairs , each being a cylindrical pin fitting a corresponding eye, the axes of all being parallel. Here each link has only motion in a circle relatively to the one next to it. Every turning of relatively to must necessarily be accompanied by alterations in the positions of and of —the chain is therefore closed. In itself a closed chain does not postulate any definite absolute motion. In order to obtain this a similar method must be adopted to the one employed above with pairs of elements,—namely, to hold fast or fix in position one linkof the chain relatively to the portion of surrounding space assumed to be stationary. The relative motions of the links then become absolute. A closed kinematic chain, of which one link is thus made stationary, is called a mechanism.
Fig. 10.
The above chain can be made a mechanism in four different ways, as shown in the following table, in which the stationary link is underlined in each case:—
| 1. | b — c | d — e | f — g | h — a |
| 2. | b — c | d — e | f — g | h — a |
| 3. | b — c | d — e | f — g | h — a |
| 4. | b — c | d — e | f — g | h — a |
In general, therefore, a constrained closed kinematic chain can be formed into a mechanism in as many ways as it has links.8
In order that a link may be made stationary it must be provided with suitably formed fastenings or carriers.
To make the demonstration complete, let us suppose that we employ a sufficiently rigid pedestal, such as that shown in Fig. 11, as a support to which one link of our chain, for example, can be clamped, so that kinematically it may form one piece with . The motion which can now take place in the chain is indicated by the dotted lines, and will be at once recognised as that of the beam and crank of a steam-engine.
The form of the pedestal or equivalent body is of course, so far as the motion is concerned, indifferent. Yet it will be noticed at once that as a rule there is a certain inclination to treat it as a piece of architecture, with which it certainly has in common the property of rest or immovability, and in the neighbourhood of which also it is often placed. The stationary parts of mechanisms have often attracted the attention of theorists. We have already seen this in the Introduction (p. 10) in Borgnis' division of the
Fig. 11.
parts of machines, where the "supports" figure as a class by themselves. Another indication of the same feeling is to be found in the division which so often occurs of the parts of machines into "active" and "passive." The latter are nothing else than the elements connected with those links of a kinematic chain which are, for the time, fixed. No absolute distinction exists however between these and the "active" parts, for in the various mechanisms constructed out of the same chain, the same part of the machine may sometimes be fixed and sometimes movable.
In the mechanisms which can be constructed out of a chain of the above-described arrangement, the motion of a link next the fixed link is determined by the nature of the element by means of which it is paired to that link; this one pair of elements alone influences its motion. With the link upon the further side of this one the case is different, its motion depends upon the motion of its neighbour-elements as well as upon the motions due to the elements at its points of attachment; in our illustration, for instance, it is influenced by four pairs of elements.
Fig. 12.
Its motion relatively to the fixed link is however as determinate as if the two were connected by one pair of elements only. Hence we can again use the method by which in the first instance we obtained the chain,—we can, that is, combine an element of a new pair with it and so further extend the chain. In order to obtain at the same time the requisite closure, this extended chain must be brought back again into connection with the link at which it started. We obtain in this way a compound kinematic chain, as distinct from which we may call the one described above a simple chain. Fig. 12 shows such a compound chain, formed of six links of exactly the same description as those used before. Two of the links now contain three elements:—
- d — i — e
- and a — h — o If we suppose a h (that is a A o) again to be
fixed, k 1 will have a yet more complex motion than
d e; the method of building up the chain further allows the
possibility of obtaining motions according to more and more com- plex laws, and so to serve as the means of procuring a great, indeed an infinite number of different forms of motion. It holds equally good with the compound as with the simple chain that it can be set in motion after fixing any one of its links; in as many ways, that is to say, as it has links.
Closed mechanisms also can again combine, and so unite into higher forms; we may however allow these compound me- chanisms to class with those built up from compound chains.
We have now before us a general view of the method of con- struction of Mechanisms:
The mechanism is a closed kinematic chain; the kine- matic chain is compound or simple, and consists of kine- matic pairs of elements; these carry the envelopes required for the motion which the bodies in contact must have, and by these all motions other than those desired in the mechanism are prevented.
A kinematic mechanism is moved if a mechanical force or effort be applied to one of its movable links in such a way as to alter its position. The effort thus applied performs mechanical work which is accompanied by determinate motions; the whole, that is to say, is a Machine.
The arrangement by which the natural force is thus brought into action must correspond to the purpose for which the machine is intended. If for example the natural force act continuously, the machine receives a continuous motion, as in water-wheels, tur- bines, and so on. If the part acted upon by the force comes after a time into such a position that the latter exercises no further influence upon it, then, if the motion is to be continued, artificial means must be provided for restoring it to a position where such influence can again be exerted; as for instance in the clock. In many machines the action is limited to very small alterations of position of the moving parts, as in the balance, after which alter- ation they must be restored to their original position. This much by way of illustration only, later on we shall have to consider these questions systematically. The title Machine has not hitherto been used logically. Commonly it is applied only in those cases where force or motion appears continuously or to some large extent. Many would not call the balance which we have just mentioned a machine, in consquence of the narrowness of the limits within which, its motion is confined; but force and motion are employed in it in exactly the same way as in other machines; it certainly ought there- fore to receive the same name. We may much rather say that the Engineer's measuring instruments, the theodolite, level and so on, are not machines. Here indeed mechanisms, in exactly the above de- scribed meaning, are used, and forces must be applied to these in just the way we have supposed in order that they may be used. The forces however are very small, and the mechanisms are only used at intervals, so that the name Instrument may properly be preferred for them. But the title Machine is even here not incorrect, as one may convince oneself by looking at the English giant telescope with its massive foundation and all the appliances for working it. With all these it differs in degree only, and not in kind, from a little pocket telescope. To such machines as occur naturally, also, the name is denied by many. Two blocks of stone which, like " dog- knee " levers, grip a third between them, may form kinematically the same combination as the train shown in Fig. 11; the so- called Eocking-stones, which have been weathered into existence in many places, are formed like balance beams; the Geysers of Iceland act in a way to a certain extent resembling the steam-engine, forcing the water through distinct vertical tubes formed by stalactitic deposits; from all these we cannot withhold the name of Machine. I mention these things, however, merely to show the avail- ability of the word for our purpose, for the strictly scientific mean- ing of the name employed cannot be a matter of indifference to us. It is far from my intention to urge the employment of the name in cases in which its use is of no importance. But the examples just given come as well within our definition of a machine as within the above demonstration of its general nature. They show also that, in spite of the non-employment of the name, it is yet perfectly correct in the circumstances we have supposed; it serves, that is to say, to indicate that they jointly possess the characteristics summed up in our definition.
We have already seen how a mechanism becomes a machine. In its complete form the machine consists of one or more mecha- nisms, which can, in the way we have already pointed out, be separated into kinematic chains, and these again into pairs of elements. This separation is the analysis of the machine, the investigation of its kinematic contents, arranged in mechanisms, kinematic chains, and pairs of elements. The reverse of this operation is synthesis, the placing together of the kinematic elements, chains and mechanisms, from which a machine can be built up so as to fulfil its required function.
There is a large region among the exact sciences in which analysis and synthesis can exist without each other, where at least important results can be obtained by the use merely of de- duction from fixed general laws. In our case, however, the two intellectual operations cannot go on separately, because the machine never, or scarcely ever, comes to us as a ready-made pro- duction of nature, but as something which we ourselves have made, because, that is, it has been created by us essentially by a synthetic method. The induction by which we have arrived at it has often been very indistinct, and hence deduction and analysis are or must become means enabling us to reach it by an induc- tion or synthesis which is conscious and definite.
The synthesis is here, as in most cases, by far the more difficult of the two processes. On this account it has scarcely ever been un- dertaken other than empirically. Its province is simply that which is assigned, in common language, to invention, and about which we spoke at length in the Introduction. Essentially, invention is nothing other than induction, a continual setting down and there- after analysing of the possible solutions which present themselves by analogy. The process continues until some more or less distinct goal is reached, a goal which generally seems itself to be indefinite on account of the haziness which envelopes the whole procedure. In this way a result lying close to the starting point is too often reached only after traversing a whole labyrinth of solutions each one depending upon the one before it, and each thrown away as soon as it has been found. I do not doubt that many of my readers, who have spent hours and days poring over mechanical problems, have found, after many laborious trials, that they have been travelling through a circle of experiment only to reach some well known, but unfortunately not so well recognised, problem. The chief cause of all this trouble is that the mechanisms are not seen, or not recognised, because their proper nature, the kinematic linkwork with its laws, has not been present in the thoughts of the mechanician. The acquaintance with this would, in nine cases out of ten, have shown him any near-lying result immediately, and would have greatly shortened the way to results further off. For the scientific theory of mechanisms, if it give a complete mastery over analysis, sweeps entirely away a great portion of the difficulties, and entirely alters the nature of those which remain. While the empirical method is only a groping in the dark in the hope that by good luck we may lay hold of the solution, we come here to the application of an inductive method, based upon a well-understood analysis. The difficulties now consist only in the increased demands upon the capacity for induction. In this itself, however, Kinematics follows its own strict laws, like all other sciences. There will be further frequent opportunity for showing how great the difference is between this method and the old one, at this point I can only place it before the reader in general propositions.
We see now the Machine-problem theoretically solved, or in other words, we have the general features of the method of solution sketched in an abstract form before us; these point out the direction in which we must work. The general propositions laid down as to pairs of elements, chains and mechanisms, are, as it were, only the titles of volumes as yet unopened, the contents of which we must now commence to study page by page; for it is necessary, in order that our solution of the problem may be brought down from general first principles to their detailed applications, that the latter should be carefully examined. This study we shall begin in the following section.
It can be readily understood that such an investigation is neither simple nor easy, to me at least it does not appear possible to pass quickly over such wide-reaching questions. Whoever attentively examines the nature of the machine, discovers in it so many phenomena having mutual relations difficult to understand that he cannot penetrate to the deep under-lying laws which connect them, and he comprehends how it has often taken the whole power of single men to carry forward even one step some of the problems which present themselves. When we consider the spinning-machine, for example, which has been gradually developing for three generations into its present form, (one still capable of further improvement), notwithstanding that the best mechanics have worked at it; or look at the changes through which the sewing-machine has passed, and examine each step by step, we can form some conception of the difficulties which the theory has to overcome. In addition to this, the propositions to be developed are completely new. They therefore require that numerous details should be carefully entered into, of which some may appear to the engineer to be already well understood, although in reality the laws upon which they depend have not yet been investigated, and in the light of these they may be seen in many new aspects. It will therefore be some time before we arrive at such propositions as are adapted for direct application.
When, however, we have gone so far as to have demonstrated these existing laws and their mutual relations, we shall have reached the limits up to which theory can be our guide.
For the right application of these laws demands certain special qualities in the designer of a machine besides a mere knowledge of its theory, if his work is to be what is called " practical," by which is meant that the required object is to be fully and permanently attained, without too great an expen- diture of means. This art of making practical work can be but very partially communicated by teaching, it can only be made quite clear by example. The scientific abstraction only serves to show the possibility of the machine, it affords no means what- ever of judging between "practical" and "unpractical." This is often cited as an essential imperfection of theory, a notion which only arises from an obstinate ignoring of its real province. We have separated the department of practice from that of ab- stract theory in order to see more clearly the complicated course of our subject. Every time, however, that we have to choose between the useful and the useless, we are compelled to return from the abstract to the concrete. In the school, therefore, kine- matic science must frequently be connected with its practical applications it has not only to show what theoretical solution applies to problems already solved empirically, but in. most cases to construct the theory as well as to find it. It is remarkable that there is scarcely any kinematic problem, scarcely any turning, however bold, in the theoretical propositions, for which we cannot find an example in practice. It must not, however, be considered that theory has only and always to limp behind practice, as is too often the case; it may rather be said to comprehend in itself all the mutual relations of the laws which in their application constitute this practice; it raises a clear flame out of each spark of truth, and so renders possible new and various roads to its higher development. The attitude of Theory and Practice to each other, in connection with the Machine, must be one of mutual respect.



























