APPENDIX III.
Proof that, if any one Proposition of Table II be granted as an Axiom, the rest can be deduced from it. (See pp. 34, 40.)
"… and so we make it quite a merry-go-rounder." I was obliged to consider a little before I understood what Mr. Peggotty meant by this figure, expressive of a complete circle of intelligence.
It is to be proved that, if any one of the Propositions of Table II be granted, the rest can be proved.
It is assumed that the lesser of two unequal finite magnitudes of the same kind may be multiplied so as to exceed the greater.
Euclid I, 1 to 28, is assumed as proved.
It is assumed that, where two Propositions are Contranominals, so that each can be proved from the other, it is not necessary to include both in the series of proofs.
Lemma 1.
A Pair of Lines, of which one contains two points equidistant from the other, have a common perpendicular.
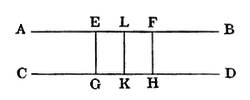
Let AB contain 2 points E, F, equidistant from CD. From E, F, draw EG, FH, ⊥ CD; bisect GH in K, and EF in L, and join KL.
Now EG = FH; [hyp.
hence, if the diagram be reversed, and so placed on its former traces that G coincides with H, and H with G, K retaining its position, GE coincides with HF, and HF with GE;
∴ E coincides with F, and F with E;
∴ L retains its position;
∴ ∠GKL coincides with ∠HKL, and is equal to it;
∴ ∠s at K are right.
Similarly ∠s at L are right.
Therefore a Pair of Lines, &c. Q. E. D.
(α). II. 1.
A Pair of separational Lines are equally inclined to any transversal.
[N.B. The Contranominal of this will be proved at the end of the series.]
(β). II. 16 (a).
Two intersecting Lines cannot both be separational from the same Line.

Let AEB, GEH be two intersecting Lines, and CD another Line. It is to be proved that they cannot both be separational from CD.
In CD take any point F; and join EF.
Now, if possible, let AB, GH both be separational from CD;
∴ ∠s AEF, GEF are both equal to ∠EFD; [(α).
∴ they are equal to each other ; which is absurd.
Therefore two intersecting Lines &c. Q. E. D.
(γ). II. 6.
A Pair of separational Lines are equidistantial from each other.

Let AB, CD be separational Lines : it shall be proved that they are equidistantial from each other.
In AB take any 2 points E, F; and draw EG, FH, ⊥ CD.
Now, if FH > EG, from it cut off KH equal to EG; and join EK;
then, ∵ EG = KH,
∴ EK, CD have a common perpendicular; [Lemma 1.
∴ EK is separational from CD; [Euc. I. 27.
∴ AB, EK, intersecting Lines, are both separational from CD ; which is absurd ; [(β)
∴ FH is not > EG.
Similarly it may be proved that EG is not > FH.
Therefore EG = FH.
Similarly it may be proved that any 2 points in AB are equidistant from CD, and that any 2 points in CD are equidistant from AB.
Therefore AB, CD are equidistantial from each other.
Therefore a Pair &c. Q. E. D.
(δ). II. 11.
A Pair of Lines, which are equally inclined to a certain transversal, are equidistantial from each other.
A Pair of Lines, which are equally inclined to a certain transversal, are separational; [Euc. I. 27.
also a Pair of separational Lines are equidistantial from each other; [(γ).
∴ a Pair of Lines, &c. Q. E. D.
(ε). II. 8.
Through a given point, without a given Line, a Line may be drawn such that the two Lines are equidistantial from each other.
For, if through the given point there be drawn a transversal, there can also be drawn through it a Line such that the two Lines make equal ∠s with the transversal; [Euc. I. 23.
and this Line will be such that the two Lines are equidistantial from each other. [(δ).
Therefore, &c. Q. E. D.
(ζ). II. 17.
A Line cannot recede from and then approach another; nor can one approach and then recede from another on the same side of it.

If possible, let ABC first recede from, and then approach, DE; that is, let the perpendicular BG be > each of the two perpendiculars AF, CH.
From GB cut off GK > each of the two, AF, CH.
Now a Line may be drawn, through K, equidistantial from DE; [(ε).
and the points A, C will lie on the side of it next to DE, and B on the other side;
∴ it will cut AB between A and B, and BC between B and C.
Let L, M be the points of intersection; and join LM;
∴ the 2 Lines LBM, LKM contain a space; which is absurd.
Similarly it may be proved that ABC cannot first approach and then recede from DE on the same side of it.
Therefore a Line &c. Q. E. D.
(η). II. 13.
A Pair of Lines, of which one has two points on the same side of, and equidistant from, the other, are eqiddistantial from each other.

Let AB contain two points E, F, equidistant from CD. From E, F, draw EG, FH, ⊥ CD; bisect GH in K, and EF in L, and join KL.
Now EG = FH; [hyp.
hence, if the diagram be reversed, and so placed on its former traces that G coincides with H, and H with G, K retaining its position, GE coincides with HF, and HF with GE;
∴ E coincides with F, and F with E;
∴ L retains its position;
∴, if there be a point in LA whose distance is < LK, there is another such point in LB, and the Line AB will first recede from and then approach CD; which is absurd. [(ζ).
Similarly if there be one whose distance is > LK.
∴ AB is equidistantial from CD.
Similarly it may be proved that CD is equidistantial from AB.
Therefore a Pair of Lines, &c. Q. E. D.
Lemma 2.
Through a given point may he drawn a common perpendicular to a given Pair of Lines, of which each is equidistantial from the other.

Let AB, CD be the given Pair of Lines.
Through the given point draw a Line perpendicular to AB, and let it meet AB in L. In AB take any 2 points E, F, equidistant from L. From E, F, draw EG, FH, perpendicular to CD. Bisect GH at K; and join KL.
Now E, F are 2 points, in AB, equidistant from CD; and GH is bisected in K, and EF in L;
∴ KL is a common perpendicular; [Lemma 1.
∴ it coincides with the Line drawn, through the given point, perpendicular to AB, since both meet AB at L;
∴ KL is the Line required.
(θ). II. 9.
A Pair of Lines, of which one has two points on the same side of, and equidistant from, the other, are equally inclined to any transversal.

Let AB contain two points equidistant from CD, and let EF be a certain transversal: it shall be proved that ∠AEF = ∠EFD.
Now AB, CD, are equidistantial from each other. [(η).
Bisect EF at G; through G let HGK be drawn a common perpendicular to AB and CD. [Lemma 2.
Hence, in Triangles GEH, GFK, side GE and ∠s EGH, GHE, are respectively equal to side GF and ∠s FGK, GKF;
∴ ∠GEH = GFK. [Euc. I. 26.
Therefore a Pair of Lines, &c. Q. E. D.
(κ). II. 3.
Through a given point, without a given Line, a Line may be drawn such that the two Lines are equally inclined to any transversal.
Take a second point, on the same side of the given Line and at the same distance from it; and join the 2 points.
Then the Line, so drawn, and the given Line, are equally inclined to any transversal. [(θ).
Therefore through a given point, &c. Q. E. D.
(λ). II. 18 (b).
The angles of a Triangle are together equal to two right angles.

Let ABC be a Triangle. It is to be proved that its 3 angles are together equal to 2 right angles.
Through A let DAE be drawn, such that DAE, BC are equally inclined to any transversal. [(κ).
Then ∠B = ∠DAB, and ∠C = ∠EAC;
∴ ∠s B, C, BAC = ∠s DAB, EAC, BAC;
= 2 rt ∠s. [Euc. I. 13.
Therefore the angles &c. Q. E. D.
(μ). II. 4.
A Pair of Lines, which are equally inclined to a certain transversal, are so to any transversal.

Let AB, CD be equally inclined to EF; and let GH be any other transversal. It shall be proved that they are equally inclined to GH.
Join EH.
Because ∠s of Triangle EFH together = 2 rt ∠s, and likewise those of Triangle EGH, [(λ).
∴ angles of Figure FG together = 4 rt angles;
also, by hypothesis, ∠s GEF, EFH together = 2 rt ∠s;
∴ remaining ∠s EGH, GHF together = 2 rt ∠s;
∴ AB, CD are equally inclined to GH.
Therefore a Pair of Lines, &c. Q. E. D.
Contranominal of (α). II. 2.
A Pair of Lines, which make with a third Line two interior angles, on one side of it, together less than two right angles, will meet on that side if produced.

Let ABC, DEF be two Triangles such that ∠s, A, D are equal, and DE, DF equimultiples of AB, AC.
From DE cut off successive parts equal to AB; and let the points of section be G, H. At G, H make ∠s equal to ∠E.
Then the Lines, so drawn, are separational from EF and from one another; [Euc. I. 28.
∴ these Lines meet DF between D and F; call these points K, L.
At G, H make ∠s equal to ∠D.
Then the Lines, so drawn, are separational from DF;
∴ they respectively meet HL between H and L, and EF between E and F; call these points M, N.

Because Triangles DGK, GHM, HEN are on equal bases and have their base-∠s respectively equal,
∴ DK, GM, HN are equal. [Euc. I. 26.
Join GL.
Because DL, GM are equally inclined to DE,
∴ they are equally inclined to GL; [(μ).
∴ ∠s KLG, LGM are equal.
Similarly, ∵ GK, HL are equally inclined to DE,
∴ they are equally inclined to GL;
∴ ∠s KGL, GLM are equal.
Because Triangles LGK, GLM are on same base LG and have their base-∠s respectively equal,
∴ KL = GM, i.e. = DK. [I. 26.
Similarly it may be proved that LF = HN, i.e. = DK.
Hence DE, DF are equimultiples of DG, DK, i.e. of AB, DK,
but they are also equimultiples of AB, AC;
∴ DK = AC.
Because Triangles ABC, DGK have ∠s A, D equal, and AB, AC respectively equal to DG, DK,
∴ ∠s, B, DGK are equal, and likewise ∠s C, DKG. [I. 4.
Because GK, EF are equally inclined to DE,
∴ they are equally inclined to DF; [(μ).
i.e. ∠s DKG, DFE are equal;
∴ ∠s B, C are respectively equal to ∠s E, F.
Hence, two Triangles, which have their vertical angles equal, and the 2 sides of the one respectively equimultiples of those of the other, have their base-angles respectively equal.

Now let AB, CD make with AC two interior ∠s BAC, ACD together < 2 right ∠s. It shall be proved that they will meet if produced towards B, D.
In CD take any point D. Join AD. At A make ∠DAH equal to ∠CBA.
Hence AH, CD are equally inclined to all transversals; [(μ).
∴ ∠s HAC, ACD together = 2 right ∠s;
∴ they together > ∠s BAC, ACD;
∴ ∠HAC > ∠BAC, i.e. ∠HAD > ∠BAD;
∴ ∠CDA > ∠BAD.
At D, in Line DA, make an ∠ equal to ∠BAD;
then the Line, so drawn, will fall within ∠CDA, and will meet CA between C and A. Call this point K.
In CA produced take CL a multiple of CK, and > CA. And in CD produced take CM the same multiple of CD that CL is of CK. And join LM.
Because Triangles CKD, CLM have a common vertical ∠, and the 2 sides of the one respectively equimultiples of those of the other,
∴, by what has been already proved, ∠s CKD, CLM are equal.
Because AB, KD are equally inclined to AD,
∴ they are equally inclined to CL; [(μ).
∴ ∠CAB = ∠CKD i.e. = ∠CLM;
∴ AB is separational from LM; [Euc. I. 28.
∴ if produced, it will meet CM.
Therefore a Pair of Lines, &c. Q. E. D.
ERRATUM.
Page 261, l. 9, for i.e. ∠ BAD read i.e. ∠ HAD > ∠ BAD;