CRYSTALLOGRAPHY (from the Gr. κρύσταλλος, ice, and γράφειν, to write), the science of the forms, properties and structure of crystals. Homogeneous solid matter, the physical and chemical properties of which are the same about every point, may be either amorphous or crystalline. In amorphous matter all the properties are the same in every direction in the mass; but in crystalline matter certain of the physical properties vary with the direction. The essential properties of crystalline matter are of two kinds, viz. the general properties, such as density, specific heat, melting-point and chemical composition, which do not vary with the direction; and the directional properties, such as cohesion and elasticity, various optical, thermal and electrical properties, as well as external form. By reason of the homogeneity of crystalline matter the directional properties are the same in all parallel directions in the mass, and there may be a certain symmetrical repetition of the directions along which the properties are the same.
When the crystallization of matter takes place under conditions free from outside influences the peculiarities of internal structure are expressed in the external form of the mass, and there results a solid body bounded by plane surfaces intersecting in straight edges, the directions of which bear an intimate relation to the internal structure. Such a polyhedron (πολύς, many, ἕδρα, base or face) is known as a crystal. An example of this is sugar-candy, of which a single isolated crystal may have grown freely in a solution of sugar. Matter presenting well-defined and regular crystal forms, either as a single crystal or as a group of individual crystals, is said to be crystallized. If, on the other hand, crystallization has taken place about several centres in a confined space, the development of plane surfaces may be prevented, and a crystalline aggregate of differently orientated crystal-individuals results. Examples of this are afforded by loaf sugar and statuary marble.
After a brief historical sketch, the more salient principles of the subject will be discussed under the following sections:—
| I. Crystalline Form. II. Physical Properties of Crystals. III. Relations between Crystalline Form and Chemical Composition. |
Most chemical elements and compounds are capable of assuming the crystalline condition. Crystallization may take place when solid matter separates from solution (e.g. sugar, salt, alum), from a fused mass (e.g. sulphur, bismuth, felspar), or from a vapour (e.g. iodine, camphor, haematite; in the last case by the interaction of ferric chloride and steam). Crystalline growth may also take place in solid amorphous matter, for example, in the devitrification of glass, and the slow change in metals when subjected to alternating stresses. Beautiful crystals of many substances may be obtained in the laboratory by one or other of these methods, but the most perfectly developed and largest crystals are those of mineral substances found in nature, where crystallization has continued during long periods of time. For this reason the physical science of crystallography has developed side by side with that of mineralogy. Really, however, there is just the same connexion between crystallography and chemistry as between crystallography and mineralogy, but only in recent years has the importance of determining the crystallographic properties of artificially prepared compounds been recognized.
History.—The word “crystal” is from the Gr. κρύσταλλος, meaning clear ice (Lat. crystallum), a name which was also applied to the clear transparent quartz (“rock-crystal”) from the Alps, under the belief that it had been formed from water by intense cold. It was not until about the 17th century that the word was extended to other bodies, either those found in nature or obtained by the evaporation of a saline solution, which resembled rock-crystal in being bounded by plane surfaces, and often also in their clearness and transparency.
The first important step in the study of crystals was made by Nicolaus Steno, the famous Danish physician, afterwards bishop of Titiopolis, who in his treatise De solido intra solidum naturaliter contento (Florence, 1669; English translation, 1671) gave the results of his observations on crystals of quartz. He found that although the faces of different crystals vary considerably in shape and relative size, yet the angles between similar pairs of faces are always the same. He further pointed out that the crystals must have grown in a liquid by the addition of layers of material upon the faces of a nucleus, this nucleus having the form of a regular six-sided prism terminated at each end by a six-sided pyramid. The thickness of the layers, though the same over each face, was not necessarily the same on different faces, but depended on the position of the faces with respect to the surrounding liquid; hence the faces of the crystal, though variable in shape and size, remained parallel to those of the nucleus, and the angles between them constant. Robert Hooke in his Micrographia (London, 1665) had previously noticed the regularity of the minute quartz crystals found lining the cavities of flints, and had suggested that they were built up of spheroids. About the same time the double refraction and perfect rhomboidal cleavage of crystals of calcite or Iceland-spar were studied by Erasmus Bartholinus (Experimenta crystalli Islandici disdiaclastici, Copenhagen, 1669) and Christiaan Huygens (Traité de la lumière, Leiden, 1690); the latter supposed, as did Hooke, that the crystals were built up of spheroids. In 1695 Anton van Leeuwenhoek observed under the microscope that different forms of crystals grow from the solutions of different salts. Andreas Libavius had indeed much earlier, in 1597, pointed out that the salts present in mineral waters could be ascertained by an examination of the shapes of the crystals left on evaporation of the water; and Domenico Guglielmini (Riflessioni filosofiche dedotte dalle figure de’ sali, Padova, 1706) asserted that the crystals of each salt had a shape of their own with the plane angles of the faces always the same.
The earliest treatise on crystallography is the Prodromus Crystallographiae of M. A. Cappeller, published at Lucerne in 1723. Crystals were mentioned in works on mineralogy and chemistry; for instance, C. Linnaeus in his Systema Naturae (1735) described some forty common forms of crystals amongst minerals. It was not, however, until the end of the 18th century that any real advances were made, and the French crystallographers Romé de l’Isle and the abbé Haüy are rightly considered as the founders of the science. J. B. L. de Romé de l’Isle (Essai de cristallographie, Paris, 1772; Cristallographie, ou description des formes propres à tous les corps du règne minéral, Paris, 1783) made the important discovery that the various shapes of crystals of the same natural or artificial substance are all intimately related to each other; and further, by measuring the angles between the faces of crystals with the goniometer (q.v.), he established the fundamental principle that these angles are always the same for the same kind of substance and are characteristic of it. Replacing by single planes or groups of planes all the similar edges or solid angles of a figure called the “primitive form” he derived other related forms. Six kinds of primitive forms were distinguished, namely, the cube, the regular octahedron, the regular tetrahedron, a rhombohedron, an octahedron with a rhombic base, and a double six-sided pyramid. Only in the last three can there be any variation in the angles: for example, the primitive octahedron of alum, nitre and sugar were determined by Romé de l’Isle to have angles of 110°, 120° and 100° respectively. René Just Haüy in his Essai d’une théorie sur la structure des crystaux (Paris, 1784; see also his Treatises on Mineralogy and Crystallography, 1801, 1822) supported and extended these views, but took for his primitive forms the figures obtained by splitting crystals in their directions of easy fracture of “cleavage,” which are aways the same in the same kind of substance. Thus he found that all crystals of calcite, whatever their external form (see, for example, figs. 1-6 in the article Calcite), could be reduced by cleavage to a rhombohedron with interfacial angles of 75°. Further, by stacking together a number of small rhombohedra of uniform size he was able, as had been previously done by J. G. Gahn in 1773, to reconstruct the various forms of calcite crystals. Fig. 1 shows a scalenohedron (σκαληνός, uneven) built up in this manner of rhombohedra; and fig. 2 a regular octahedron built up of cubic elements, such as are given by the cleavage of galena and rock-salt.
 | |
| Fig. 1.—Scalenohedron built up of Rhombohedra. |
Fig. 2.—Octahedron built up of Cubes. |
The external surfaces of such a structure, with their step-like arrangement, correspond to the plane faces of the crystal, and the bricks may be considered so small as not to be separately visible. By making the steps one, two or three bricks in width and one, two or three bricks in height the various secondary faces on the crystal are related to the primitive form or “cleavage nucleus” by a law of whole numbers, and the angles between them can be arrived at by mathematical calculation. By measuring with the goniometer the inclinations of the secondary faces to those of the primitive form Haüy found that the secondary forms are always related to the primitive form on crystals of numerous substances in the manner indicated, and that the width and the height of a step are always in a simple ratio, rarely exceeding that of 1 : 6. This laid the foundation of the important “law of rational indices” of the faces of crystals.
The German crystallographer C. S. Weiss (De indagando formarum crystallinarum charactere geometrico principali dissertatio, Leipzig, 1809; Übersichtliche Darstellung der verschiedenen natürlichen Abtheilungen der Krystallisations-Systeme, Denkschrift der Berliner Akad. der Wissensch., 1814–1815) attacked the problem of crystalline form from a purely geometrical point of view, without reference to primitive forms or any theory of structure. The faces of crystals were considered by their intercepts on co-ordinate axes, which were drawn joining the opposite corners of certain forms; and in this way the various primitive forms of Haüy were grouped into four classes, corresponding to the four systems described below under the names cubic, tetragonal, hexagonal and orthorhombic. The same result was arrived at independently by F. Mohs, who further, in 1822, asserted the existence of two additional systems with oblique axes. These two systems (the monoclinic and anorthic) were, however, considered by Weiss to be only hemihedral or tetartohedral modifications of the orthorhombic system, and they were not definitely established until 1835, when the optical characters of the crystals were found to be distinct. A system of notation to express the relation of each face of a crystal to the co-ordinate axes of reference was devised by Weiss, and other notations were proposed by F. Mohs, A. Lévy (1825), C. F. Naumann (1826), and W. H. Miller (Treatise on Crystallography, Cambridge, 1839). For simplicity and utility in calculation the Millerian notation, which was first suggested by W. Whewell in 1825, surpasses all others and is now generally adopted, though those of Lévy and Naumann are still in use.
Although the peculiar optical properties of Iceland-spar had been much studied ever since 1669, it was not until much later that any connexion was traced between the optical characters of crystals and their external form. In 1818 Sir David Brewster found that crystals could be divided optically into three classes, viz. isotropic, uniaxial and biaxial, and that these classes corresponded with Weiss’s four systems (crystals belonging to the cubic system being isotropic, those of the tetragonal and hexagonal being uniaxial, and the orthorhombic being biaxial). Optically biaxial crystals were afterwards shown by J. F. W. Herschel and F. E. Neumann in 1822 and 1835 to be of three kinds, corresponding with the orthorhombic, monoclinic and anorthic systems. It was, however, noticed by Brewster himself that there are many apparent exceptions, and the “optical anomalies” of crystals have been the subject of much study. The intimate relations existing between various other physical properties of crystals and their external form have subsequently been gradually traced.
The symmetry of crystals, though recognized by Romé de l’Isle and Haüy, in that they replaced all similar edges and corners of their primitive forms by similar secondary planes, was not made use of in defining the six systems of crystallization, which depended solely on the lengths and inclinations of the axes of reference. It was, however, necessary to recognize that in each system there are certain forms which are only partially symmetrical, and these were described as hemihedral and tetartohedral forms (i.e. ἡμι-, half-faced, and τέταρτος, quarter-faced forms).
As a consequence of Haüy’s law of rational intercepts, or, as it is more often called, the law of rational indices, it was proved by J. F. C. Hessel in 1830 that thirty-two types of symmetry are possible in crystals. Hessel’s work remained overlooked for sixty years, but the same important result was independently arrived at by the same method by A. Gadolin in 1867. At the present day, crystals are considered as belonging to one or other of thirty-two classes, corresponding with these thirty-two types of symmetry, and are grouped in six systems. More recently, theories of crystal structure have attracted attention, and have been studied as purely geometrical problems of the homogeneous partitioning of space.
The historical development of the subject is treated more fully in the article Crystallography in the 9th edition of this work. Reference may also be made to C. M. Marx, Geschichte der Crystallkunde (Karlsruhe and Baden, 1825); W. Whewell, History of the Inductive Sciences, vol. iii. (3rd ed., London, 1857); F. von Kobell, Geschichte der Mineralogie von 1650–1860 (München, 1864); L. Fletcher, An Introduction to the Study of Minerals (British Museum Guide-Book); L. Fletcher, Recent Progress in Mineralogy and Crystallography [1832–1894] (Brit. Assoc. Rep., 1894).
The fundamental laws governing the form of crystals are:—
1. Law of the Constancy of Angle.
2. Law of Symmetry.
3. Law of Rational Intercepts or Indices.
According to the first law, the angles between corresponding faces of all crystals of the same chemical substance are always the same and are characteristic of the substance.
(a) Symmetry of Crystals.
Crystals may, or may not, be symmetrical with respect to a point, a line or axis, and a plane; these “elements of symmetry” are spoken of as a centre of symmetry, an axis of symmetry, and a plane of symmetry respectively.
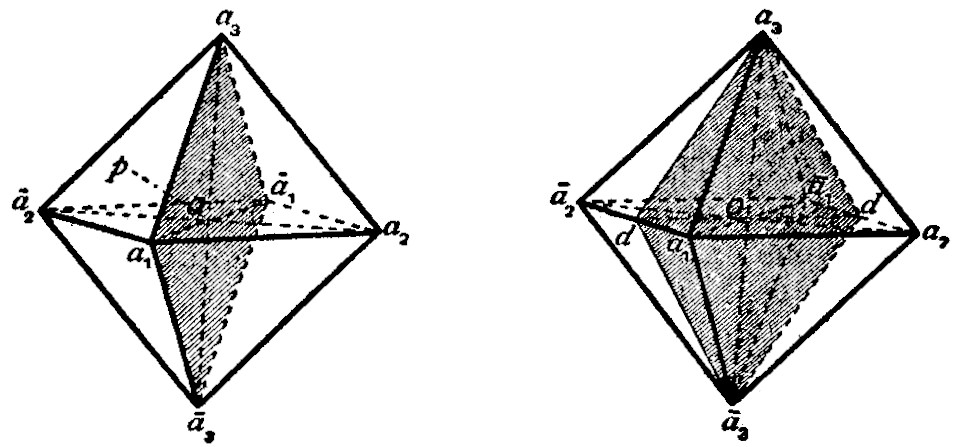
Centre of Symmetry.—Crystals which are centro-symmetrical have their faces arranged in parallel pairs; and the two parallel faces, situated on opposite sides of the centre (O in fig. 3) are alike in surface characters, such as lustre, striations, and figures of corrosion. An octahedron (fig. 3) is bounded by four pairs of parallel faces. Crystals belonging to many of the hemihedral and tetartohedral classes of the six systems of crystallization are devoid of a centre of symmetry.
Axes of Symmetry.—Consider the vertical axis joining the opposite corners a3 and ā3 of an octahedron (fig. 3) and passing through its centre O: by rotating the crystal about this axis through a right angle (90°) it reaches a position such that the orientation of its faces is the same as before the rotation; the face ā1ā2ā3, for example, coming into the position of a1ā2a3. During a complete rotation of 360° (= 90° × 4), the crystal occupies four such interchangeable positions. Such an axis of symmetry is known as a tetrad axis of symmetry. Other tetrad axes of the octahedron are a2ā2 and a1a1.
An axis of symmetry of another kind is that which passing through the centre O is normal to a face of the octahedron. By rotating the crystal about such an axis Op (fig. 3) through an angle of 120° those faces which are not perpendicular to the axis occupy interchangeable positions; for example, the face a1a3a2 comes into the position of ā2a1ā3, and ā2a1ā3 to a3ā2ā1. During a complete rotation of 360° (= 120° × 3) the crystal occupies similar positions three times. This is a triad axis of symmetry; and there being four pairs of parallel faces on an octahedron, there are four triad axes (only one of which is drawn in the figure).
 | |
| Fig. 3. | Fig. 4. |
| Axes and Planes of Symmetry of an Octahedron. | |
An axis passing through the centre O and the middle points d of two opposite edges of the octahedron (fig. 4), i.e. parallel to the edges of the octahedron, is a dyad axis of symmetry. About this axis there may be rotation of 180°, and only twice in a complete revolution of 360° (= 180° × 2) is the crystal brought into interchangeable positions. There being six pairs of parallel edges on an octahedron, there are consequently six dyad axes of symmetry.
A regular octahedron thus possesses thirteen axes of symmetry (of three kinds), and there are the same number in the cube. Fig. 5 shows the three tetrad (or tetragonal) axes (aa), four triad (or trigonal) axes (pp), and six dyad (diad or diagonal) axes (dd).
Although not represented in the cubic system, there is still another kind of axis of symmetry possible in crystals. This is the hexad axis or hexagonal axis, for which the angle of rotation is 60°, or one-sixth of 360°. There can be only one hexad axis of symmetry in any crystal (see figs. 77-80).
 |
| Fig. 5.—Axes of Symmetry of a Cube. |
Planes of Symmetry.—A regular octahedron can be divided into two equal and similar halves by a plane passing through the corners a1a3ā1ā3 and the centre O (fig. 3). One-half is the mirror reflection of the other in this plane, which is called a plane of symmetry. Corresponding planes on either side of a plane of symmetry are inclined to it at equal angles. The octahedron can also be divided by similar planes of symmetry passing through the corners a1a2ā1ā2 and a2a3ā2ā3. These three similar planes of symmetry are called the cubic planes of symmetry, since they are parallel to the faces of the cube (compare figs. 6-8, showing combinations of the octahedron and the cube).
A regular octahedron can also be divided symmetrically into two equal and similar portions by a plane passing through the corners a3 and ā3, the middle points d of the edges a1ā2 and ā1a2, and the centre O (fig. 4). This is called a dodecahedral plane of symmetry, being parallel to the face of the rhombic dodecahedron which truncates the edge a1a2 (compare fig. 14, showing a combination of the octahedron and rhombic dodecahedron). Another similar plane of symmetry is that passing through the corners a3ā3 and the middle points of the edges a1a2 and ā1ā2, and altogether there are six dodecahedral planes of symmetry,
two through each of the corners a1, a2, a3 of the octahedron. A regular octahedron and a cube are thus each symmetrical with respect to the following elements of symmetry: a centre of symmetry, thirteen axes of symmetry (of three kinds), and nine planes of symmetry (of two kinds). This degree of symmetry, which is the type corresponding to one of the classes of the cubic system, is the highest possible in crystals. As will be pointed out below, it is possible, however, for both the octahedron and the cube to be associated with fewer elements of symmetry than those just enumerated.
(b) Simple Forms and Combinations of Forms.
A single face a1a2a3 (figs. 3 and 4) may be repeated by certain of the elements of symmetry to give the whole eight faces of the octahedron. Thus, by rotation about the vertical tetrad axis a3ā3 the four upper faces are obtained; and by rotation of these about one or other of the horizontal tetrad axes the eight faces are derived. Or again, the same repetition of the faces may be arrived at by reflection across the three cubic planes of symmetry. (By reflection across the six dodecahedral planes of symmetry a tetrahedron only would result, but if this is associated with a centre of symmetry we obtain the octahedron.) Such a set of similar faces, obtained by symmetrical repetition, constitutes a "simple form." An octahedron thus consists of eight similar faces, and a cube is bounded by six faces all of which have the same surface characters, and parallel to each of which all the properties of the crystal are identical.
 | |
| Fig. 6.—Cube in combination with Octahedron. |
Fig. 7.—Cubo-octahedron. |
 |
| Fig. 8.—Octahedron in combination with Cube. |
Examples of simple forms amongst crystallized substances are octahedra of alum and spinel and cubes of salt and fluorspar. More usually, however, two or more forms are present on a crystal, and we then have a combination of forms, or simply a "combination." Figs. 6, 7 and 8 represent combinations of the octahedron and the cube; in the first the faces of the cube predominate, and in the third those of the octahedron; fig. 7 with the two forms equally developed is called a cubo-octahedron. Each of these combined forms has all the elements of symmetry proper to the simple forms.
The simple forms, though referable to the same type of symmetry and axes of reference, are quite independent, and cannot be derived one from the other by symmetrical repetition, but, after the manner of Romé de l'Isle, they may be derived by replacing edges or corners by a face equally inclined to the faces forming the edges or corners; this is known as "truncation" (Lat. truncare, to cut off). Thus in fig. 6 the corners of the cube are symmetrically replaced or truncated by the faces of the octahedron, and in fig. 8 those of the octahedron are truncated by the cube.
(c) Law of Rational Intercepts.
For axes of reference, OX, OY, OZ (fig. 9), take any three edges formed by the intersection of three faces of a crystal. These axes are called the crystallographic axes, and the planes in which they lie the axial planes. A fourth face on the crystal intersecting these three axes in the points A, B, C is taken as the parametral plane, and the lengths OA: OB: OC are the parameters of the crystal. Any other face on the crystal may be referred to these axes and parameters by the ratio of the intercepts
| OA | : | OB | : | OC | . |
| h | k | l |
Thus for a face parallel to the plane A Be the intercepts are in the ratio OA: OB: Oe, or
| OA | : | OB | : | OC |
| 1 | 1 | 2 |
and for a plane fgC they are Of: Og: OC or
| OA | : | OB | : | OC | . |
| 2 | 3 | 1 |
Now the important relation existing between the faces of a crystal is that the denominators h, k and l are always rational whole numbers, rarely exceeding 6, and usually 0, 1, 2 or 3. Written in the form (hkl), h referring to the axis OX, k to OY, and l to OZ, they are spoken of as the indices (Millerian indices) of the face. Thus of a face parallel to the plane ABC the indices are (111), of ABe they are (112), and of fgC (231). The indices are thus inversely proportional to the intercepts, and the law of rational intercepts is often spoken of as the "law of rational indices."
The angular position of a face is thus completely fixed by its indices; and knowing the angles between the axial planes and the parametral plane all the angles of a crystal can be calculated when the indices of the faces are known.
 |
| Fig. 9.—Crystallographic axes of reference. |
Although any set of edges formed by the intersection of three planes may be chosen for the crystallographic axes, it is in practice usual to select certain edges related to the symmetry of the crystal, and usually coincident with axes of symmetry; for then the indices will be simpler and all faces of the same simple form will have a similar set of indices. The angles between the axes and the ratio of the lengths of the parameters OA: OB: OC (usually given as a: b: c) are spoken of as the "elements" of a crystal, and are constant for and characteristic of all crystals of the same substance.
The six systems of crystal forms, to be enumerated below, are defined by the relative inclinations of the crystallographic axes and the lengths of the parameters. In the cubic system, for example, the three crystallographic axes are taken parallel to the three tetrad axes of symmetry, i.e. parallel to the edges of the cube (fig. 5) or joining the opposite corners of the octahedron (fig. 3), and they are therefore all at right angles; the parametral plane (111) is a face of the octahedron, and the parameters are all of equal length. The indices of the eight faces of the octahedron will then be (111), (111), (111), (111), (111), (111), (111), (111). The symbol {111} indicates all the faces belonging to this simple form. The indices of the six faces of the cube are (100), (010), (001), (100), (010), (001); here each face is parallel to two axes, i.e. intercepts them at infinity, so that the corresponding indices are zero.
(d) Zones.
An important consequence of the law of rational intercepts is the arrangement of the faces of a crystal in zones. All faces, whether they belong to one or more simple forms, which intersect in parallel edges are said to lie in the same zone. A line drawn through the centre O of the crystal parallel to these edges is called a zone-axis, and a plane perpendicular to this axis is called a zone-plane. On a cube, for example, there are three zones each containing four faces, the zone-axes being coincident with the three tetrad axes of symmetry. In the crystal of zircon (fig. 88) the eight prism-faces a, m, &c. constitute a zone, denoted by [a, m, a′, &c.], with the vertical tetrad axis of symmetry as zone-axis. Again the faces [a, x, p, e′, p′, x″′, a″] lie in another zone, as may be seen by the parallel edges of intersection of the faces in figs. 87 and 88; three other similar zones may be traced on the same crystal.
The direction of the line of intersection (i.e. zone-axis) of any two planes (hkl) and (h1k1l1) is given by the zone-indices [uvw], where u = kl1 − lk1, v = lh1 − hl1, and w = hk1 − kh1, these being obtained from the face-indices by cross multiplication as follows:—
| h | k | l | h | k | l |
××× | |||||
| h1 | k1 | l1 | h1 | k1 | l1 |
Any other face (h2k2l2) lying in this zone must satisfy the equation
This important relation connecting the indices of a face lying in a zone with the zone-indices is known as Weiss’s zone-law, having been first enunciated by C. S. Weiss. It may be pointed out that the indices of a face may be arrived at by adding together the indices of faces on either side of it and in the same zone; thus, (311) in fig. 12 lies at the intersections of the three zones [210, 101], [201, 110] and [211, 100], and is obtained by adding together each set of indices.
(e) Projection and Drawing of Crystals.
The shapes and relative sizes of the faces of a crystal being as a rule accidental, depending only on the distance of the faces from the centre of the crystal and not on their angular relations, it is often more convenient to consider only the directions of the normals to the faces. For this purpose projections are drawn, with the aid of which the zonal relations of a crystal are more readily studied and calculations are simplified.
 |
| Fig. 10.—Stereographic Projection of a Cubic Crystal. |
 |
| Fig. 11.—Clinographic Drawing of a Cubic Crystal. |
The kind of projection most extensively used is the “stereographic projection.” The crystal is considered to be placed inside a sphere from the centre of which normals are drawn to all the faces of the crystal. The points at which these normals intersect the surface of the sphere are called the poles of the faces, and by these poles the positions of the faces are fixed. The poles of all faces in the same zone on the crystal will lie on a great circle of the sphere, which are therefore called zone-circles. The calculation of the angles between the normals of faces and between zone-circles is then performed by the ordinary methods of spherical trigonometry. The stereographic projection, however, represents the poles and zone-circles on a plane surface and not on a spherical surface. This is achieved by drawing lines joining all the poles of the faces with the north or south pole of the sphere and finding their points of intersection with the plane of the equatorial great circle, or primitive circle, of the sphere, the projection being represented on this plane. In fig. 10 is shown the stereographic projection, or stereogram, of a cubic crystal; a1, a2, &c. are the poles of the faces of the cube. o1, o2, &c. those of the octahedron, and d1, d2, &c. those of the rhombic dodecahedron. The straight lines and circular arcs are the projections on the equatorial plane of the great circles in which the nine planes of symmetry intersect the sphere. A drawing of a crystal showing a combination of the cube, octahedron and rhombic dodecahedron is shown in fig. 11, in which the faces are lettered the same as the corresponding poles in the projection. From the zone-circles in the projection and the parallel edges in the drawing the zonal relations of the faces are readily seen: thus [a1o1d5], [a1d1a5], [a5o1d2], &c. are zones. A stereographic projection of a rhombohedral crystal is given in fig. 72.
Another kind of projection in common use is the “gnomonic projection” (fig. 12). Here the plane of projection is tangent to the sphere, and normals to all the faces are drawn from the centre of the sphere to intersect the plane of projection. In this case all zones are represented by straight lines. Fig. 12 is the gnomonic projection of a cubic crystal, the plane of projection being tangent to the sphere at the pole of an octahedral face (111), which is therefore in the centre of the projection. The indices of the several poles are given in the figure.
 |
| Fig. 12.—Gnomonic Projection of a Cubic Crystal. |
In drawing crystals the simple plans and elevations of descriptive geometry (e.g. the plans in the lower part of figs. 87 and 88) have sometimes the advantage of showing the symmetry of a crystal, but they give no idea of solidity. For instance, a cube would be represented merely by a square, and an octahedron by a square with lines joining the opposite corners. True perspective drawings are never used in the representation of crystals, since for showing the zonal relations it is important to preserve the parallelism of the edges. If, however, the eye, or point of vision, is regarded as being at an infinite distance from the object all the rays will be parallel, and edges which are parallel on the crystal will be represented by parallel lines in the drawing. The plane of the drawing, in which the parallel rays joining the corners of the crystals and the eye intersect, may be either perpendicular or oblique to the rays; in the former case we have an “orthographic” (ὀρθός, straight; γράφειν, to draw) drawing, and in the latter a “clinographic” (κλίνειν, to incline) drawing. Clinographic drawings are most frequently used for representing crystals. In representing, for example, a cubic crystal (fig. 11) a cube face a5 is first placed parallel to the plane on which the crystal is to be projected and with one set of edges vertical; the crystal is then turned through a small angle about a vertical axis until a second cube face a2 comes into view, and the eye is then raised so that a third cube face a1 may be seen.
(f) Crystal Systems and Classes.
According to the mutual inclinations of the crystallographic axes of reference and the lengths intercepted on them by the parametral plane, all crystals fall into one or other of six groups or systems, in each of which there are several classes depending on the degree of symmetry. In the brief description which follows of these six systems and thirty-two classes of crystals we shall proceed from those in which the symmetry is most complex to those in which it is simplest.
1. CUBIC SYSTEM
In this system the three crystallographic axes of reference are all at right angles to each other and are equal in length. They are parallel to the edges of the cube, and in the different classes coincide either with tetrad or dyad axes of symmetry. Five classes are included in this system, in all of which there are, besides other elements of symmetry, four triad axes.
In crystals of this system the angle between any two faces P and Q with the indices (hkl) and (pqr) is given by the equation
| COS PQ = | hp + kq + lr | . |
| √(h² + k² + l²) (p² + q² + r²) |
The angles between faces with the same indices are thus the same in all substances which crystallize in the cubic system: in other systems the angles vary with the substance and are characteristic of it.
Holosymmetric Class
Crystals of this class possess the full number of elements of symmetry already mentioned above for the octahedron and the cube, viz. three cubic planes of symmetry, six dodecahedral planes, three tetrad axes of symmetry, four triad axes, six dyad axes, and a centre of symmetry.
 | |
| Fig. 13.—Rhombic Dodecahedron. | Fig. 14.—Combination of Rhombic Dodecahedron and Octahedron. |
There are seven kinds of simple forms, viz.:—
Cube (fig. 5). This is bounded by six square faces parallel to the cubic planes of symmetry; it is known also as the hexahedron. The angles between the faces are 90°, and the indices of the form are {100}. Salt, fluorspar and galena crystallize in simple cubes.
 | |
| Fig. 15.—Triakis-octahedron. | Fig. 16.—Combination of Triakis-octahedron and Cube. |
Octahedron (fig. 3). Bounded by eight equilateral triangular faces perpendicular to the triad axes of symmetry. The angles between the faces are 70° 32′ and 109° 28′, and the indices are {111}. Spinel, magnetite and gold crystallize in simple octahedra. Combinations of the cube and octahedron are shown in figs. 6-8.
Rhombic dodecahedron (fig. 13). Bounded by twelve rhomb-shaped faces parallel to the six dodecahedral planes of symmetry. The angles between the normals to adjacent faces are 60°, and between other pairs of faces 90°; the indices are {110}. Garnet frequently crystallizes in this form. Fig. 14 shows the rhombic dodecahedron in combination with the octahedron.
 | |
| Fig. 17.—Icositetrahedron. | Fig. 18.—Combination of Icositetrahedron and Cube. |
In these three simple forms of the cubic system (which are shown in combination in fig. 11) the angles between the faces and the indices are fixed and are the same in all crystals; in the four remaining simple forms they are variable.
 | |
| Fig. 19.—Combination of Icositetrahedron and Octahedron. |
Fig. 20.—Combination of Icositetrahedron {211} and Rhombic Dodecahedron. |
Triakis-octahedron (three-faced octahedron) (fig. 15). This solid is bounded by twenty-four isosceles triangles, and may be considered as an octahedron with a low triangular pyramid on each of its faces. As the inclinations of the faces may vary there is a series of these forms with the indices {221}, {331}, {332}, &c. or in general {hhk}.
 | |
| Fig. 21.—Tetrakis-hexahedron. | Fig. 22.—Tetrakis-hexahedron. |
Icositetrahedron (fig. 17). Bounded by twenty-four trapezoidal faces, and hence sometimes called a “trapezohedron.” The indices are {211}, {311}, {322}, &c., or in general {hkk}. Analcite, leucite and garnet often crystallize in the simple form {211}. Combinations are shown in figs. 18-20. The plane ABe in fig. 9 is one face (112) of an icositetrahedron; the indices of the remaining faces in this octant being (211) and (121).
 |
| Fig. 23.—Combination of Tetrakis-hexahedron and Cube. |
Tetrakis-hexahedron (four-faced cube) (figs. 21 and 22). Like the triakis-octahedron this solid is also bounded by twenty-four isosceles triangles, but here grouped in fours over the cubic faces. The two figures show how, with different inclinations of the faces, the form may vary, approximating in fig. 21 to the cube and in fig. 22 to the rhombic dodecahedron. The angles over the edges lettered A are different from the angles over the edges lettered C. Each face is parallel to one of the crystallographic axes and intercepts the two others in different lengths; the indices are therefore {210}, {310}, {320}, &c., in general {hko}. Fluorspar sometimes crystallizes in the simple form {310}; more usually, however, in combination with the cube (fig. 23).
Hexakis-octahedron (fig. 24). Here each face of the octahedron is replaced by six scalene triangles, so that altogether there are forty-eight faces. This is the greatest number of faces possible for any simple form in crystals. The faces are all oblique to the planes and axes of symmetry, and they intercept the three crystallographic axes in different lengths, hence the indices are all unequal, being in general {hkl}, or in particular cases {321}, {421}, {432}, &c. Such a form is known as the “general form” of the class. The interfacial angles over the three edges of each triangle are all different. These forms usually exist only in combination with other cubic forms (for example, fig. 25), but {421} has been observed as a simple form on fluorspar.
 | |
| Fig. 24.—Hexakis-octahedron. | Fig. 25.—Combination of Hexakis-octahedron and Cube. |
Several examples of substances which crystallize in this class have been mentioned above under the different forms; many others might be cited—for instance, the metals iron, copper, silver, gold, platinum, lead, mercury, and the non-metallic elements silicon and phosphorus.
Tetrahedral Class
In this class there is no centre of symmetry nor cubic planes of symmetry; the three tetrad axes become dyad axes of symmetry, and the four triad axes are polar, i.e. they are associated with different faces at their two ends. The other elements of symmetry (six dodecahedral planes and six dyad axes) are the same as in the last class.
 | |
| Fig. 26.—Tetrahedron. | Fig. 27.—Deltoid Dodecahedron. |
Of the seven simple forms, the cube, rhombic dodecahedron and tetrakis-hexahedron are geometrically the same as before, though on actual crystals the faces will have different surface characters. For instance, the cube faces will be striated parallel to only one of the diagonals (fig. 90), and etched figures on this face will be symmetrical with respect to two lines, instead of four as in the last class. The remaining simple forms have, however, only half the number of faces as the corresponding form in the last class, and are spoken of as “hemihedral with inclined faces.”
 | |
| Fig. 28.—Triakis-tetrahedron. | Fig. 29.—Hexakis-tetrahedron. |
Tetrahedron (fig. 26). This is bounded by four equilateral triangles and is identical with the regular tetrahedron of geometry. The angles between the normals to the faces are 109° 28′. It may be derived from the octahedron by suppressing the alternate faces.
Deltoid[1] dodecahedron (fig. 27). This is the hemihedral form of the triakis-octahedron; it has the indices {hhk} and is bounded by twelve trapezoidal faces.
Triakis-tetrahedron (fig. 28). The hemihedral form {hkk} of the icositetrahedron; it is bounded by twelve isosceles triangles arranged in threes over the tetrahedron faces.
 | |
| Fig. 30.—Combination of two Tetrahedra. |
Fig. 31.—Combination of Tetrahedron and Cube. |
Hexakis-tetrahedron (fig. 29). The hemihedral form {hkl} of the hexakis-octahedron; it is bounded by twenty-four scalene triangles and is the general form of the class.
 | |
| Fig. 32.—Combination of Tetrahedron, Cube and Rhombic Dodecahedron. |
Fig. 33.—Combination of Tetrahedron and Rhombic Dodecahedron. |
Corresponding to each of these hemihedral forms there is another geometrically similar form, differing, however, not only in orientation, but also in actual crystals in the characters of the faces. Thus from the octahedron there may be derived two tetrahedra with the indices {111} and {111}, which may be distinguished as positive and negative respectively. Fig. 30 shows a combination of these two tetrahedra, and represents a crystal of blende, in which the four larger faces are dull and striated, whilst the four smaller are bright and smooth. Figs. 31-33 illustrate other tetrahedral combinations.
Tetrahedrite, blende, diamond, boracite and pharmacosiderite are substances which crystallize in this class.
Pyritohedral[2] Class
Crystals of this class possess three cubic planes of symmetry but no dodecahedral planes. There are only three dyad axes of symmetry, which coincide with the crystallographic axes; in addition there are three triad axes and a centre of symmetry.
 | |
| Fig. 34. Pentagonal Dodecahedron. | Fig. 35. Dyakis-dodecahedron. |
Here the cube, octahedron, rhombic dodecahedron, triakis-octahedron and icositetrahedron are geometrically the same as in the first class. The characters of the faces will, however, be different; thus the cube faces will be striated parallel to one edge only (fig. 89), and triangular markings on the octahedron faces will be placed obliquely to the edges. The remaining simple forms are “hemihedral with parallel faces,” and from the corresponding holohedral forms two hemihedral forms, a positive and a negative, may be derived.
Pentagonal dodecahedron (fig. 34). This is bounded by twelve pentagonal faces, but these are not regular pentagons, and the angles over the three sets of different edges are different. The regular dodecahedron of geometry, contained by twelve regular pentagons, is not a possible form in crystals. The indices are {hko}: as a simple form {210} is of very common occurrence in pyrites.
Dyakis-dodecahedron (fig. 35). This is the hemihedral form of the hexakis-octahedron and has the indices {hkl}; it is bounded by twenty-four faces. As a simple form {321} is met with in pyrites.
 | |
| Fig. 36.—Combination of Pentagonal Dodecahedron and Cube. |
Fig. 37.—Combination of Pentagonal Dodecahedron and Octahedron. |
Combinations (figs. 36-39) of these forms with the cube and the octahedron are common in pyrites. Fig. 37 resembles in general appearance the regular icosahedron of geometry, but only eight of the faces are equilateral triangles. Cobaltite, smaltite and other sulphides and sulpharsenides of the pyrites group of minerals crystallize in these forms. The alums also belong to this class; from an aqueous solution they crystallize as simple octahedra, sometimes with subordinate faces of the cube and rhombic dodecahedron, but from an acid solution as octahedra combined with the pentagonal dodecahedron {210}.
 | |
| Fig. 38.—Combination of Pentagonal Dodecahedron, Cube and Octahedron. |
Fig. 39.—Combination of Pentagonal Dodecahedron e {210}, Dyakis-dodecahedron f {321}, and Octahedron d {111}. |
Plagihedral[3] Class
In this class there are the full number of axes of symmetry (three tetrad, four triad and six dyad), but no planes of symmetry and no centre of symmetry.
 | |
| Fig. 40.—Pentagonal Icositetrahedron. |
Fig. 41.—Tetrahedral Pentagonal Dodecahedron. |
Pentagonal icositetrahedron (fig. 40). This is the only simple form in this class which differs geometrically from those of the holosymmetric class. By suppressing either one or other set of alternate faces of the hexakis-octahedron two pentagonal icositetrahedra {hkl} and {khl} are derived. These are each bounded by twenty-four irregular pentagons, and although similar to each other they are respectively right- and left-handed, one being the mirror image of the other; such similar but nonsuperposable forms are said to be enantiomorphous (ἐναντίος, opposite, and μορφή, form), and crystals showing such forms sometimes rotate the plane of polarization of plane-polarized light. Faces of a pentagonal icositetrahedron with high indices have been very rarely observed on crystals of cuprite, potassium chloride and ammonium chloride, but none of these are circular polarizing.
Tetartohedral Class
Here, in addition to four polar triad axes, the only other elements of symmetry are three dyad axes, which coincide with the crystallographic axes. Six of the simple forms, the cube, tetrahedron, rhombic dodecahedron, deltoid dodecahedron, triakis-tetrahedron and pentagonal dodecahedron, are geometrically the same in this class as in either the tetrahedral or pyritohedral classes. The general form is the Tetrahedral pentagonal dodecahedron (fig. 41). This is bounded by twelve irregular pentagons, and is a tetartohedral or quarter-faced form of the hexakis-octahedron. Four such forms may be derived, the indices of which are {hkl}, {khl}, {hkl} and {khl}; the first pair are enantiomorphous with respect to one another, and so are the last pair. Barium nitrate, lead nitrate, sodium chlorate and sodium bromate crystallize in this class, as also do the minerals ullmannite (NiSbS) and langbeinite (K2Mg2(SO4)3).
In this system the three crystallographic axes are all at right angles, but while two are equal in length and interchangeable the third is of a different length. The unequal axis is spoken of as the principal axis or morphological axis of the crystal, and it is always placed in a vertical position; in five of the seven classes of this system it coincides with the single tetrad axis of symmetry.
 |
 |
| Fig. 42. | Fig. 43. |
| Tetragonal Bipyramids. | |
The parameters are a : a : c, where a refers to the two equal horizontal axes, and c to the vertical axis; c may be either shorter (as in fig. 42) or longer (fig. 43) than a. The ratio a : c is spoken of as the axial ratio of a crystal, and it is dependent on the angles between the faces. In all crystals of the same substance this ratio is constant, and is characteristic of the substance; for other substances crystallizing in the tetragonal system it will be different. For example, in cassiterite it is given as a : c = 1 : 0.67232 or simply as c = 0.67232, a being unity; and in anatase as c = 1.7771.
Holosymmetric Class
Crystals of this class are symmetrical with respect to five planes, which are of three kinds; one is perpendicular to the principal axis, and the other four intersect in it; of the latter, two are perpendicular to the equal crystallographic axes, while the two others bisect the angles between them. There are five axes of symmetry, one tetrad and two pairs of dyad, each perpendicular to a plane of symmetry. Finally, there is a centre of symmetry.
There are seven kinds of simple forms, viz.:—
Tetragonal bipyramid of the first order (figs. 42 and 43). This is bounded by eight equal isosceles triangles. Equal lengths are intercepted on the two horizontal axes, and the indices are {111}, {221}, {112}, &c., or in general {hhl}. The parametral plane with the intercepts a : a : c is a face of the bipyramid {111}.
 | |
| Fig. 44. | Fig. 45. |
| Tetragonal Bipyramids of the first and second orders. | |
Tetragonal bipyramid of the second order. This is also bounded by eight equal isosceles triangles, but differs from the last form in its position, four of the faces being parallel to each of the horizontal axes; the indices are therefore {101}, {201}, {102}, &c., or {hol}.
Fig. 44 shows the relation between the tetragonal bipyramids of the first and second orders when the indices are {111} and {101} respectively: ABB is the face (111), and ACC is (101). A combination of these two forms is shown in fig. 45.
 |
| Fig. 46.—Ditetragonal Bipyramid. |
Ditetragonal bipyramid (fig. 46). This is the general form; it is bounded by sixteen scalene triangles, and all the indices are unequal, being {321}, &c., or {hkl}.
Tetragonal prism of the first order. The four faces intersect the horizontal axes in equal lengths and are parallel to the principal axis; the indices are therefore {110}. This form does not enclose space, and is therefore called an “open form” to distinguish it from a “closed form” like the tetragonal bipyramids and all the forms of the cubic system. An open form can exist only in combination with other forms; thus fig. 47 is a combination of the tetragonal prism {110} with the basal pinacoid {001}. If the faces (110) and (001) are of equal size such a figure will be geometrically a cube, since all the angles are right angles; the variety of apophyllite known as tesselite crystallizes in this form.
Tetragonal prism of the second order. This has the same number of faces as the last prism, but differs in position; each face being parallel to the vertical axis and one of the horizontal axes; the indices are {100}.
Ditetragonal prism. This consists of eight faces all parallel to the principal axis and intercepting the horizontal axes in different lengths; the indices are {210}, {320}, &c., or {hko}.
Basal pinacoid (from πίναξ, a tablet). This consists of a single pair of parallel faces perpendicular to the principal axis. It is therefore an open form and can exist only in combination (fig. 47).
 |
 |
 |
| Fig. 47. Combination of Tetragonal Prism and Basal Pinacoid. |
Fig. 48. | Fig. 49. |
| Combinations of Tetragonal Prisms and Pyramids. | ||
Combinations of holohedral tetragonal forms are shown in figs. 47–49; fig. 48 is a combination of a bipyramid of the first order with one of the second order and the prism of the first order; fig. 49 a combination of a bipyramid of the first order with a ditetragonal bipyramid and the prism of the second order. Compare also figs. 87 and 88.
Examples of substances which crystallize in this class are cassiterite, rutile, anatase, zircon, thorite, vesuvianite, apophyllite, phosgenite, also boron, tin, mercuric iodide.
Scalenohedral Class
Here there are only three dyad axes and two planes of symmetry, the former coinciding with the crystallographic axes and the latter bisecting the angles between the horizontal pair. The dyad axis of symmetry, which in this class coincides with the principal axis of the crystal, has certain of the characters of a tetrad axis, and is sometimes called a tetrad axis of “alternating symmetry”; a face on the upper half of the crystal if rotated through 90° about this axis and reflected across the equatorial plane falls into the position of a face on the lower half of the crystal. This kind of symmetry, with simultaneous rotation about an axis and reflection across a plane, is also called “composite symmetry.”
In this class all except two of the simple forms are geometrically the same as in the holosymmetric class.
Bisphenoid (σφήν, a wedge) (fig. 50). This is a double wedge-shaped solid bounded by four equal isosceles triangles; it has the indices {111}, {211}, {112}, &c., or in general {hhl}. By suppressing either one or other set of alternate faces of the tetragonal bipyramid of the first order (fig. 42) two bisphenoids are derived, in the same way that two tetrahedra are derived from the regular octahedron.
Tetragonal scalenohedron or ditetragonal bisphenoid (fig. 51). This is bounded by eight scalene triangles and has the indices {hkl}. It may be considered as the hemihedral form of the ditetragonal bipyramid.
 | |
| Fig. 50.—Tetragonal Bisphenoids. |
Fig. 51.—Tetragonal Scalenohedron. |
The crystal of chalcopyrite (CuFeS2) represented in fig. 52 is a combination of two bisphenoids (P and P′), two bipyramids of the second order (b and c), and the basal pinacoid (a). Stannite (Cu2FeSnS4), acid potassium phosphate (H2KPO4), mercuric cyanide, and urea (CO(NH2)2) also crystallize in this class.
Bipyramidal Class
The elements of symmetry are a tetrad axis with a plane perpendicular to it, and a centre of symmetry. The simple forms are the same here as in the holosymmetric class, except the prism {hko}, which has only four faces, and the bipyramid {hkl}, which has eight faces and is distinguished as a “tetragonal pyramid of the third order.”
 | |
| Fig. 52.—Crystal of Chalcopyrite. |
Fig. 53.—Crystal of Fergusonite. |
Fig. 53 shows a combination of a tetragonal prism of the first order with a tetragonal bipyramid of the third order and the basal pinacoid, and represents a crystal of fergusonite. Scheelite (q.v.), Scapolite (q.v.), and erythrite (C4H10O4) also crystallize in this class.
Pyramidal Class
Here the only element of symmetry is the tetrad axis. The pyramids of the first {hhl}, second {hol} and third {hkl} orders have each only four faces at one or other end of the crystal, and are hemimorphic. All the simple forms are thus open forms.
Examples are wulfenite (PbMoO4) and barium antimonyl dextro-tartrate (Ba(SbO)2(C4H4O6)·H2O).
Ditetragonal Pyramidal Class
Here there are two pairs of vertical planes of symmetry intersecting in the tetrad axis. The pyramids {hhl} and {hol} and the bipyramid {hkl} are all hemimorphic.
Examples are iodosuccimide (C4H4O2NI), silver fluoride (AgF·H2O), and penta-erythrite (C5H12O4). No examples are known amongst minerals.
Trapezohedral Class
Here there are the full number of axes of symmetry, but no planes or centre of symmetry. The general form {hkl} is bounded by eight trapezoidal faces and is the tetragonal trapezohedron.
Examples are nickel sulphate (NiSO4·6H2O), guanidine carbonate ((CH5N3)2H2CO3), strychnine sulphate ((C21H22N2O2)2·H2SO4·6H2O).
Bisphenoidal Class
Here there is only a single dyad axis of symmetry, which coincides with the principal axis. All the forms, except the prisms and basal pinacoid, are sphenoids. Crystals possessing this type of symmetry have not yet been observed.
In this system the three crystallographic axes are all at right angles, but they are of different lengths and not interchangeable. The parameters, or axial ratios, are a : b : c, these referring to the axes OX, OY and OZ respectively. The choice of a vertical axis, OZ = c, is arbitrary, and it is customary to place the longer of the two horizontal axes from left to right (OY = b) and take it as unity: this is called the “macro-axis” or “macro-diagonal” (from μακρός, long), whilst the shorter horizontal axis (OX = a) is called the “brachy-axis” or “brachy-diagonal” (from βραχύς, short). The axial ratios are constant for crystals of any one substance and are characteristic of it; for example, in barytes (BaSO4), a : b : c = 0.8152 : 1 : 1.3136; in anglesite (PbSO4), a : b : c = 0.7852: 1 : 1.2894; in cerussite (PbCO3), a : b : c = 0.6100 : 1 : 0.7230.
There are three symmetry-classes in this system:—
Holohedral Class
Here there are three dissimilar dyad axes of symmetry, each coinciding with a crystallographic axis; perpendicular to them are three dissimilar planes of symmetry; there is also a centre of symmetry. There are seven kinds of simple forms:—
 | |
| Fig. 54. | Fig. 55. |
| Orthorhombic Bipyramids. | |
Bipyramid (figs. 54 and 55). This is the general form and is bounded by eight scalene triangles; the indices are {111}, {211}, {221}, {112}, {321}, {123}, &c., or in general {hkl}. The crystallographic axes join opposite corners of these pyramids and in the fundamental bipyramid {111} the parametral plane has the intercepts a : b : c. This is the only closed form in this class; the others are open forms and can exist only in combination. Sulphur often crystallizes in simple bipyramids.
Prism. This consists of four faces parallel to the vertical axis and intercepting the horizontal axes in the lengths a and b or in any multiples of these; the indices are therefore {110}, {210}, {120} or {hko}.
 | |
| Fig. 56.—Macro-prism and Brachy-pinacoid. |
Fig. 57.—Brachy-prism and Macro-pinacoid. |
Macro-prism. This consists of four faces parallel to the macro-axis, and has the indices {101}, {201} ... or {hol}.
Brachy-prism. This consists of four faces parallel to the brachy-axis, and has the indices {011}, {021} ... {okl}. The macro- and brachy-prisms are often called “domes.”
Basal pinacoid, consisting of a pair of parallel faces perpendicular to the vertical axis; the indices are {001}. The macro-pinacoid {100} and the brachy-pinacoid {010} each consist of a pair of parallel faces respectively parallel to the macro- and the brachy-axis.
Figs. 56-58 show combinations of these six open forms, and fig. 59 a combination of the macro-pinacoid (a), brachy-pinacoid (b), a prism (m), a macro-prism (d), a brachy-prism (k), and a bipyramid (u).
 | |
| Fig. 58.—Prism and Basal Pinacoid. |
Fig. 59.—Crystal of Hypersthene. |
| Holohedral Orthorhombic Combinations. | |
Examples of substances crystallizing in this class are extremely numerous; amongst minerals are sulphur, stibnite, cerussite, chrysoberyl, topaz, olivine, nitre, barytes, columbite and many others; and amongst artificial products iodine, potassium permanganate, potassium sulphate, benzene, barium formate, &c.
Pyramidal Class
Here there is only one dyad axis in which two planes of symmetry intersect. The crystals are usually so placed that the dyad axis coincides with the vertical crystallographic axis, and the planes of symmetry are also vertical.
The pyramid {hkl} has only four faces at one end or other of the crystal. The macro-prism and the brachy-prism of the last class are here represented by the macro-dome and brachy-dome respectively, so called because of the resemblance of the pair of equally sloped faces to the roof of a house. The form {001} is a single plane at the top of the crystal, and is called a “pedion”; the parallel pedion {001}, if present at the lower end of the crystal, constitutes a different form. The prisms {hko} and the macro- and brachy-pinacoids are geometrically the same in this class as in the last. Crystals of this class are therefore differently developed at the two ends and are said to be “hemimorphic.”
 | |
| Fig. 60.—Crystal of Hemimorphite. |
Fig. 61.—Orthorhombic Bisphenoid. |
Fig. 60 shows a crystal of the mineral hemimorphite (H2Zn2SiO5) which is a combination of the brachy-pinacoid {010} and a prism, with the pedion (001), two brachy-domes and two macro-domes at the upper end, and a pyramid at the lower end. Examples of other substances belonging to this class are struvite (NH4MgPO4·6H2O), bertrandite (H2Be4Si2O9), resorcin, and picric acid.
Bisphenoidal Class
Here there are three dyad axes, but no planes of symmetry and no centre of symmetry. The general form {hkl} is a bisphenoid (fig. 61) bounded by four scalene triangles. The other simple forms are geometrically the same as in the holosymmetric class.
Examples: epsomite (Epsom salts, MgSO4·7H2O), goslarite (ZnSO4·7H2O), silver nitrate, sodium potassium dextro-tartrate (seignette salt, NaKC4H4O6·4H2O), potassium antimonyl dextro-tartrate (tartar-emetic, K(SbO)C4H4O6), and asparagine (C4H8N2O8·H2O).
In this system two of the angles between the crystallographic axes are right angles, but the third angle is oblique, and the axes are of unequal lengths. The axis which is perpendicular to the other two is taken as OY = b (fig. 62) and is called the ortho-axis or ortho-diagonal. The choice of the other two axes is arbitrary; the vertical axis (OZ = c) is usually taken parallel to the edges of a prominently developed prismatic zone, and the clino-axis or clino-diagonal (OX = a) parallel to the zone-axis of some other prominent zone on the crystal. The acute angle between the axes OX and OZ is usually denoted as β, and it is necessary to know its magnitude, in addition to the axial ratios a : b : c, before the crystal is completely determined. As in other systems, except the cubic, these elements, a : b : c and β, are characteristic of the substance. Thus for gypsum a : b : c = 0.6899 : 1 : 0.4124; β = 80° 42′; for orthoclase a : b : c = 0.6585 : 1 : 0.5554; β = 63° 57′; and for cane-sugar a : b : c = 1.2595 : 1 : 0.8782; β = 76° 30′.
Holosymmetric Class
Here there is a single plane of symmetry perpendicular to which is a dyad axis; there is also a centre of symmetry. The dyad axis coincides with the ortho-axis OY, and the vertical axis OZ and the clino-axis OX lie in the plane of symmetry.
 | |
| Fig. 62.—Monoclinic Axes and Hemi-pyramid. |
Fig. 63.—Crystal of Augite. |
All the forms are open, being either pinacoids or prisms; the former consisting of a pair of parallel faces, and the latter of four faces intersecting in parallel edges and with a rhombic cross-section. The pair of faces parallel to the plane of symmetry is distinguished as the “clino-pinacoid” and has the indices {010}. The other pinacoids are all perpendicular to the plane of symmetry (and parallel to the ortho-axis); the one parallel to the vertical axis is called the “ortho-pinacoid” {100}, whilst that parallel to the clino-axis is the “basal pinacoid” {001}; pinacoids not parallel to the arbitrarily chosen clino- and vertical axes may have the indices {101}, {201}, {102} ... {hol} or {101}, {201}, {102} ... {hol}, according to whether they lie in the obtuse or the acute axial angle. Of the prisms, those with edges (zone-axis) parallel to the clino-axis, and having indices {011}, {021}, {012} ... {okl}, are called “clino-prisms”; those with edges parallel to the vertical axis, and with the indices {110}, {210}, {120} ... {hko}, are called simply “prisms.” Prisms with edges parallel to neither of the axes OX and OY have the indices {111}, {221}, {211}, {321} ... {hkl} or {111} ... {hkl}, and are usually called “hemi-pyramids” (fig. 62); they are distinguished as negative or positive according to whether they lie in the obtuse or the acute axial angle β.
Fig. 63 represents a crystal of augite bounded by the clino-pinacoid (l), the ortho-pinacoid (r), a prism (M), and a hemi-pyramid (s).
The substances which crystallize in this class are extremely numerous: amongst minerals are gypsum, orthoclase, the amphiboles, pyroxenes and micas, epidote, monazite, realgar, borax, mirabilite (Na2SO4·10H2O), melanterite (FeSO4·7H2O) and many others; amongst artificial products are monoclinic sulphur, barium chloride (BaCl2·2H2O), potassium chlorate, potassium ferrocyanide (K4Fe(CN)6·3H2O), oxalic acid (C2O4H2·2H2O), sodium acetate (NaC2H3O2·3H2O) and naphthalene.
Hemimorphic Class
In this class the only element of symmetry is a single dyad axis, which is polar in character, being dissimilar at the two ends.
The form {010} perpendicular to the axis of symmetry consists of a single plane or pedion; the parallel face is dissimilar in character and belongs to the pedion {010}. The pinacoids {100}, {001}, {hol} and {hol} parallel to the axis of symmetry are geometrically the same in this class as in the holosymmetric class. The remaining forms consist each of only two planes on the same side of the axial plane XOZ and equally inclined to the dyad axis (e.g. in fig. 62 the two planes XYZ and XYZ); such a wedge-shaped form is sometimes called a sphenoid.
 |
| Fig. 64.—Enantiomorphous Crystals of Tartaric Acid. |
Fig. 64 shows two crystals of tartaric acid, a a right-handed crystal of dextro-tartaric acid, and b a left-handed crystal of laevo-tartaric acid. The two crystals are enantiomorphous, i.e. although they have the same interfacial angles they are not superposable, one being the mirror image of the other. Other examples are potassium dextro-tartrate, cane-sugar, milk-sugar, quercite, lithium sulphate (Li2SO4·H2O); amongst minerals the only example is the hydrocarbon fichtelite (C5H8).
Clinohedral Class
Crystals of this class are symmetrical only with respect to a single plane. The only form which is here geometrically the same as in the holosymmetric class is the clino-pinacoid {010}. The forms perpendicular to the plane of symmetry are all pedions, consisting of single planes with the indices {100}, {100}, {001}, {001}, {hol}, &c. The remaining forms, {hko}, {okl} and {hkl}, are domes or “gonioids” (γωνία, an angle, and εἶδος, form), consisting of two planes equally inclined to the plane of symmetry.
Examples are potassium tetrathionate (K2S4O6), hydrogen trisodium hypophosphate (HNa3P2O6·9H2O); and amongst minerals, clinohedrite (H2ZnCaSiO4) and scolectite.
In the anorthic (from ἀν, privative, and ὀρθός, right) or triclinic system none of the three crystallographic axes are at right angles, and they are all of unequal lengths. In addition to the parameters a : b : c, it is necessary to know the angles, α, β, and γ, between the axes. In anorthite, for example, these elements are a : b : c = 0.6347 : 1 : 0.5501; α = 93° 13′, β = 115° 55′, γ = 91° 12′.
Holosymmetric Class
Here there is only a centre of symmetry. All the forms are pinacoids, each consisting of only two parallel faces. The indices of the three pinacoids parallel to the axial planes are {100}, {010} and {001}; those of pinacoids parallel to only one axis are {hko}, {hol} and {okl}; and the general form is {hkl}.
 |
| Fig. 65.—Crystal of Axinite. |
Several minerals crystallize in this class; for example, the plagioclastic felspars, microcline, axinite (fig. 65), cyanite, amblygonite, chalcanthite (CuSO4·5H2O), sassolite (H3BO3); among artificial substances are potassium bichromate, racemic acid (C4H6O6·2H2O), dibrom-para-nitrophenol, &c.
Asymmetric Class
Crystals of this class are devoid of any elements of symmetry. All the forms are pedions, each consisting of a single plane; they are thus hemihedral with respect to crystals of the last class. Although there is a total absence of symmetry, yet the faces are arranged in zones on the crystals.
Examples are calcium thiosulphate (CaS2O3·6H2O) and hydrogen strontium dextro-tartrate ((C4H4O6H)2Sr·5H2O); there is no example amongst minerals.
Crystals of this system are characterized by the presence of a single axis of either triad or hexad symmetry, which is spoken of as the “principal” or “morphological” axis. Those with a triad axis are grouped together in the rhombohedral or trigonal division, and those with a hexad axis in the hexagonal division. By some authors these two divisions are treated as separate systems; or again the rhombohedral forms may be considered as hemihedral developments of the hexagonal. On the other hand, hexagonal forms may be considered as a combination of two rhombohedral forms.
Owing to the peculiarities of symmetry associated with a single triad or hexad axis, the crystallographic axes of reference are different in this system from those used in the five other systems of crystals. Two methods of axial representation are in common use; rhombohedral axes being usually used for crystals of the rhombohedral division, and hexagonal axes for those of the hexagonal division; though sometimes either one or the other set is employed in both divisions.
Rhombohedral axes are taken parallel to the three sets of edges of a rhombohedron (fig. 66). They are inclined to one another at equal oblique angles, and they are all equally inclined to the principal axis; further, they are all of equal length and are interchangeable. With such a set of axes there can be no statement of an axial ratio, but the angle between the axes (or some other angle which may be calculated from this) may be given as a constant of the substance. Thus in calcite the rhombohedral angle (the angle between two faces of the fundamental rhombohedron) is 74° 55′, or the angle between the normal to a face of this rhombohedron and the principal axis is 44° 3612′.
Hexagonal axes are four in number, viz. a vertical axis coinciding with the principal axis of the crystal, and three horizontal axes inclined to one another at 60° in a plane perpendicular to the principal axis. The three horizontal axes, which are taken either parallel or perpendicular to the faces of a hexagonal prism (fig. 71) or the edge of a hexagonal bipyramid (fig. 70), are equal in length (a) but the vertical axis is of a different length (c). The indices of planes referred to such a set of axes are four in number; they are written as {hikl}, the first three (h + i + k = 0) referring to the horizontal axes and the last to the vertical axis. The ratio a : c of the parameters, or the axial ratio, is characteristic of all the crystals of the same substance. Thus for beryl (including emerald) a : c = 1 : 0.4989 (often written c = 0.4989); for zinc c = 1.3564.
In the rhombohedral or trigonal division of the hexagonal system there are seven symmetry-classes, all of which possess a single triad axis of symmetry.
Holosymmetric Class
In this class, which presents the commonest type of symmetry of the hexagonal system, the triad axis is associated with three similar planes of symmetry inclined to one another at 60° and intersecting in the triad axis; there are also three similar dyad axes, each perpendicular to a plane of symmetry, and a centre of symmetry. The seven simple forms are:—
 |
| Fig. 66.Fig. 67. |
| Direct and Inverse Rhombohedra. |
 |
| Fig. 68.—Scalenohedron. |
Rhombohedron (figs. 66 and 67), consisting of six rhomb-shaped faces with the edges all of equal lengths: the faces are perpendicular to the planes of symmetry. There are two sets of rhombohedra, distinguished respectively as direct and inverse; those of one set (fig. 66) are brought into the orientation of the other set (fig. 67) by a rotation of 60° or 180° about the principal axis. For the fundamental rhombohedron, parallel to the edges of which are the crystallographic axes of reference, the indices are {100}. Other rhombohedra may have the indices {211}, {411}, {110}, {221}, {111}, &c., or in general {hkk}. (Compare fig. 72; for figures of other rhombohedra see Calcite.)
Scalenohedron (fig. 68), bounded by twelve scalene triangles, and with the general indices {hkl}. The zig-zag lateral edges coincide with the similar edges of a rhombohedron, as shown in fig. 69; if the indices of the inscribed rhombohedron be {100}, the indices of the scalenohedron represented in the figure are {201}. The scalenohedron {201} is a characteristic form of calcite, which for this reason is sometimes called “dog-tooth-spar.” The angles over the three edges of a face of a scalenohedron are all different; the angles over three alternate polar edges are more obtuse than over the other three polar edges. Like the two sets of rhombohedra, there are also direct and inverse scalenohedra, which may be similar in form and angles, but different in orientation and indices.
Hexagonal bipyramid (fig. 70), bounded by twelve isosceles triangles each of which are equally inclined to two planes of symmetry. The indices are {210}, {412}, &c., or in general (hkl), where h − 2k + l = 0.
|
|
Hexagonal prism of the first order (211), consisting of six faces parallel to the principal axis and perpendicular to the planes of symmetry; the angles between (the normals to) the faces are 60°.
Hexagonal prism of the second order (101), consisting of six faces parallel to the principal axis and parallel to the planes of symmetry. The faces of this prism are inclined to 30° to those of the last prism.
Dihexagonal prism, consisting of twelve faces parallel to the principal axis and inclined to the planes of symmetry. There are two sets of angles between the faces. The indices are {321}, {532} ... {hkl}, where h + k + l = 0.
Basal pinacoid {111}, consisting of a pair of parallel faces perpendicular to the principal axis.
 |
| Fig. 72.—Stereographic Projection of a Holosymmetric Rhombohedral Crystal. |
Fig. 71 shows a combination of a hexagonal prism (m) with the basal pinacoid (c). For figures of other combinations see Calcite and Corundum. The relation between rhombohedral forms and their indices are best studied with the aid of a stereographic projection (fig. 72); in this figure the thicker lines are the projections of the three planes of symmetry, and on these lie the poles of the rhombohedra (six of which are indicated).
Numerous substances, both natural and artificial, crystallize in this class; for example, calcite, chalybite, calamine, corundum (ruby and sapphire), haematite, chabazite; the elements arsenic, antimony, bismuth, selenium, tellurium and perhaps graphite; also ice, sodium nitrate, thymol, &c.
Ditrigonal Pyramidal Class
Here there are three similar planes of symmetry intersecting in the triad axis; there are no dyad axes and no centre of symmetry. The triad axis is uniterminal and polar, and the crystals are differently developed at the two ends; crystals of this class are therefore pyro-electric. The forms are all open forms:—
 |
| Fig. 73.—Crystal of Tourmaline. |
Trigonal pyramid {hkk}, consisting of the three faces which correspond to the three upper or the three lower faces of a rhombohedron of the holosymmetric class.
Ditrigonal pyramid {hkl}, of six faces, corresponding to the six upper or lower faces of the scalenohedron.
Hexagonal pyramid (hkl) where (h − 2k + l = 0), of six faces, corresponding to the six upper or lower faces of the hexagonal bipyramid.
Trigonal prism {211} or {211}, two forms each consisting of three faces parallel to principal axis and perpendicular to the planes of symmetry.
Hexagonal prism {101}, which is geometrically the same as in the last class.
Ditrigonal prism {hkl} (where h + k + l = 0), of six faces parallel to the principal axis, and with two sets of angles between them.
Basal pedion (111) or (111), each consisting of a single plane perpendicular to the principal axis.
Fig. 73 represents a crystal of tourmaline with the trigonal prism (211), hexagonal prism (101), and a trigonal pyramid at each end. Other substances crystallizing in this class are pyrargyrite, proustite, iodyrite (AgI), greenockite, zincite, spangolite, sodium lithium sulphate, tolylphenylketone.
Trapezohedral Class
Here there are three similar dyad axes inclined to one another at 60° and perpendicular to the triad axis. There are no planes or centre of symmetry. The dyad axes are uniterminal, and are pyro-electric axes. Crystals of most substances of this class rotate the plane of polarization of a beam of light.
 | |
| Fig. 74.—Trigonal Trapezohedron. |
Fig. 75.—Trigonal Bipyramid. |
In this class the rhombohedra {hkk}, the hexagonal prism {211}, and the basal pinacoid {111} are geometrically the same as in the holosymmetric class; the trigonal prism {101} and the ditrigonal prisms are as in the ditrigonal pyramidal class. The remaining simple forms are:—
Trigonal trapezohedron (fig. 74), bounded by six trapezoidal faces. There are two complementary and enantiomorphous trapezohedra, {hkl} and {hlk}, derivable from the scalenohedron.
Trigonal bipyramid (fig. 75), bounded by six isosceles triangles; the indices are {hkl}, where h − 2k + l = 0, as in the hexagonal bipyramid.
The only minerals crystallizing in this class are quartz (q.v.) and cinnabar, both of which rotate the plane of a beam of polarized light transmitted along the triad axis. Other examples are dithionates of lead (PbS2O6·4H2O), calcium and strontium, and of potassium (K2S2O6), benzil, matico-stearoptene.
Rhombohedral Class
The only elements of symmetry are the triad axis and a centre of symmetry. The general form {hkl} is a rhombohedron, and is a hemihedral form, with parallel faces, of the scalenohedron. The form {hkl}, where h − 2k + l = 0, is also a rhombohedron, being the hemihedral form of the hexagonal bipyramid. The dihexagonal prism {hkl} of the holosymmetric class becomes here a hexagonal prism. The rhombohedra (hkk), hexagonal prisms {211} and {101}, and the basal pinacoid {111} are geometrically the same in this class as in the holosymmetric class.
Fig. 76 represents a crystal of dioptase with the fundamental rhombohedron r {100} and the hexagonal prism of the second order m {101} combined with the rhombohedron s {031}.
Examples of minerals which crystallize in this class are phenacite, dioptase, willemite, dolomite, ilmenite and pyrophanite: amongst artificial substances is ammonium periodate ((NH4)4I2O9·3H2O).
Trigonal Pyramidal Class
 |
| Fig. 76.—Crystal of Dioptase. |
Here there is only the triad axis of symmetry, which is uniterminal. The general form {hkl} is a trigonal pyramid consisting of three faces at one end of the crystal. All other forms, in which the faces are neither parallel nor perpendicular to the triad axis, are trigonal pyramids. All the prisms are trigonal prisms; and perpendicular to these are two pedions.
The only substance known to crystallize in this class is sodium periodate (NaIO4·3H2O), the crystals of which are circularly polarizing.
Trigonal Bipyramidal Class
Here there is a plane of symmetry perpendicular to the triad axis. The trigonal pyramids of the last class are here trigonal bipyramids (fig. 75); the prisms are all trigonal prisms, and parallel to the plane of symmetry is the basal pinacoid. No example is known for this class.
Ditrigonal Bipyramidal Class
Here there are three similar planes of symmetry intersecting in the triad axis, and perpendicular to them is a fourth plane of symmetry; at the intersection of the three vertical planes with the horizontal plane are three similar dyad axes; there is no centre of symmetry.
 |
| Fig. 77.—Dihexagonal Bipyramid. |
The general form is bounded by twelve scalene triangles and is a ditrigonal bipyramid. Like the general form of the last class, this has two sets of indices {hkl, pqr}, (hkl) for faces above the equatorial plane of symmetry and (pqr) for faces below: with hexagonal axes there would be only one set of indices. The hexagonal bipyramids, the hexagonal prism {101} and the basal pinacoid {111} are geometrically the same in this class as in the holosymmetric class. The trigonal prism {211} and ditrigonal prisms {hkl} are the same as in the ditrigonal pyramidal class.
The only representative of this type of symmetry is the mineral benitoite (q.v.).
In crystals of this division of the hexagonal system the principal axis is a hexad axis of symmetry. Hexagonal axes of reference are used: if rhombohedral axes be used many of the simple forms will have two sets of indices.
Holosymmetric Class
Intersecting in the hexad axis are six planes of symmetry of two kinds, and perpendicular to them is an equatorial plane of symmetry. Perpendicular to the hexad axis are six dyad axes of two kinds and each perpendicular to a vertical plane of symmetry. The seven simple forms are:—
Dihexagonal bipyramid, bounded by twenty-four scalene triangles (fig. 77; v in fig. 80). The indices are {2131}, &c., or in general {hikl}. This form may be considered as a combination of two scalenohedra, a direct and an inverse.
 | ||
| Fig. 78. | Fig. 79. | Fig. 80. |
| Combinations of Hexagonal forms. | ||
Hexagonal bipyramid of the first order, bounded by twelve isosceles triangles (fig. 70; p and u in fig. 80); indices {1011}, {2021} ... (hohl). The hexagonal bipyramid so common in quartz is geometrically similar to this form, but it really is a combination of two rhombohedra, a direct and an inverse, the faces of which differ in surface characters and often also in size.
Hexagonal bipyramid of the second order, bounded by twelve faces (s in figs. 79 and 80); indices {1121}, {1122} ... {h.h.2h.l }.
Dihexagonal prism, consisting of twelve faces parallel to the hexad axis and inclined to the vertical planes of symmetry; indices {hiko}.
Hexagonal prism of the first order {1010}, consisting of six faces parallel to the hexad axis and perpendicular to one set of three vertical planes of symmetry (m in figs. 71, 78-80).
Hexagonal prism of the second order {1120}, consisting of six faces also parallel to the hexad axis, but perpendicular to the other set of three vertical planes of symmetry (a in fig. 78).
Basal pinacoid {0001}, consisting of a pair of parallel planes perpendicular to the hexad axis (c in figs. 71, 78-80).
Beryl (emerald), connellite, zinc, magnesium and beryllium crystallize in this class.
Bipyramidal Class
Here there is a plane of symmetry perpendicular to the hexad axis; there is also a centre of symmetry. All the closed forms are hexagonal bipyramids; the open forms are hexagonal prisms or the basal pinacoid. The general form {hikl} is hemihedral with parallel faces with respect to the general form of the holosymmetric class.
Apatite (q.v.), pyromorphite, mimetite and vanadinite possess this degree of symmetry.
Dihexagonal Pyramidal Class
Six planes of symmetry of two kinds intersect in the hexad axis. The hexad axis is uniterminal and all the forms are open forms. The general form {hikl} consists of twelve faces at one end of the crystal, and is a dihexagonal pyramid. The hexagonal pyramids {hohl} and (h.h.2h.l) each consist of six faces at one end of the crystal. The prisms are geometrically the same as in the holosymmetric class. Perpendicular to the hexad axis are the pedions (0001) and (0001).
Iodyrite (AgI), greenockite (CdS), wurtzite (ZnS) and zincite (ZnO) are often placed in this class, but they more probably belong to the hemimorphic-hemihedral class of the rhombohedral division of this system.
Trapezohedral Class
Six dyad axes of two kinds are perpendicular to the hexad axis. The general form {hikl} is the hexagonal trapezohedron bounded by twelve trapezoidal faces. The other simple forms are geometrically the same as in the holosymmetric class. Barium-anti-monyldextro-tartrate + potassium nitrate (Ba(SbO)2(C4H4O6)2·KNO3) and the corresponding lead salt crystallize in this class.
Hexagonal Pyramidal Class
No other element is here associated with the hexad axis, which is uniterminal. The pyramids all consist of six faces at one end of the crystal, and prisms are all hexagonal prisms; perpendicular to the hexad axis are the pedions.
Lithium potassium sulphate, strontium-antimonyl dextro-tartrate, and lead-antimonyl dextro-tartrate are examples of this type of symmetry. The mineral nepheline is placed in this class because of the absence of symmetry in the etched figures on the prism faces (fig. 92).
(g) Regular Grouping of Crystals.
Crystals of the same kind when occurring together may sometimes be grouped in parallel position and so give rise to special structures, of which the dendritic (from δένδρον, a tree) or branch-like aggregations of native copper or of magnetite and the fibrous structures of many minerals furnish examples. Sometimes, owing to changes in the surrounding conditions, the crystal may continue its growth with a different external form or colour, e.g. sceptre-quartz.
Regular intergrowths of crystals of totally different substances such as staurolite with cyanite, rutile with haematite, blende with chalcopyrite, calcite with sodium nitrate, are not uncommon. In these cases certain planes and edges of the two crystals are parallel. (See O. Mügge, “Die regelmässigen Verwachsungen von Mineralien verschiedener Art,” Neues Jahrbuch für Mineralogie, 1903, vol. xvi. pp. 335–475).
But by far the most important kind of regular conjunction of crystals is that known as “twinning.” Here two crystals or individuals of the same kind have grown together in a certain symmetrical manner, such that one portion of the twin may be brought into the position of the other by reflection across a plane or by rotation about an axis. The plane of reflection is called the twin-plane, and is parallel to one of the faces, or to a possible face, of the crystal: the axis of rotation, called the twin-axis, is parallel to one of the edges or perpendicular to a face of the crystal.
 | |
| Fig. 81.—Twinned Crystal of Gypsum. |
Fig. 82.—Simple Crystal of Gypsum. |
In the twinned crystal of gypsum represented in fig. 81 the two portions are symmetrical with respect to a plane parallel to the ortho-pinacoid (100), i.e. a vertical plane perpendicular to the face b. Or we may consider the simple crystal (fig. 82) to be cut in half by this plane and one portion to be rotated through 180° about the normal to the same plane. Such a crystal (fig. 81) is therefore described as being twinned on the plane (100).
An octahedron (fig. 83) twinned on an octahedral face (111) has the two portions symmetrical with respect to a plane parallel to this face (the large triangular face in the figure); and either portion may be brought into the position of the other by a rotation through 180° about the triad axis of symmetry which is perpendicular to this face. This kind of twinning is especially frequent in crystals of spinel, and is consequently often referred to as the “spinel twin-law.”
In these two examples the surface of the union, or composition-plane, of the two portions is a regular surface coinciding with the twin-plane; such twins are called “juxtaposition-twins.” In other juxtaposed twins the plane of composition is, however, not necessarily the twin-plane. Another type of twin is the “interpenetration twin,” an example of which is shown in fig. 84. Here one cube may be brought into the position of the other by a rotation of 180° about a triad axis, or by reflection across the octahedral plane which is perpendicular to this axis; the twin-plane is therefore (111).
 | |
| Fig. 83.—Spinel-twin. | Fig. 84.—Interpenetrating Twinned Cubes. |
Since in many cases twinned crystals may be explained by the rotation of one portion through two right angles, R. J. Haüy introduced the term “hemitrope” (from the Gr. ἡμι-, half, and τρόπος, a turn); the word “macle” had been earlier used by Romé d’Isle. There are, however, some rare types of twins which cannot be explained by rotation about an axis, but only by reflection across a plane; these are known as “symmetric twins,” a good example of which is furnished by one of the twin-laws of chalcopyrite.
Twinned crystals may often be recognized by the presence of re-entrant angles between the faces of the two portions, as may be seen from the above figures. In some twinned crystals (e.g. quartz) there are, however, no re-entrant angles. On the other hand, two crystals accidentally grown together without any symmetrical relation between them will usually show some re-entrant angles, but this must not be taken to indicate the presence of twinning.
Twinning may be several times repeated on the same plane or on other similar planes of the crystal, giving rise to triplets, quartets and other complex groupings. When often repeated on the same plane, the twinning is said to be “polysynthetic,” and gives rise to a laminated structure in the crystal. Sometimes such a crystal (e.g. of corundum or pyroxene) may be readily broken in this direction, which is thus a “plane of parting,” often closely resembling a true cleavage in character. In calcite and some other substances this lamellar twinning may be produced artificially by pressure (see below, Sect. II. (a), Glide-plane).
Another curious result of twinning is the production of forms which apparently display a higher degree of symmetry than that actually possessed by the substance. Twins of this kind are known as “mimetic-twins or pseudo-symmetric twins.” Two hemihedral or hemimorphic crystals (e.g. of diamond or of hemimorphite) are often united in twinned position to produce a group with apparently the same degree of symmetry as the holosymmetric class of the same system. Or again, a substance crystallizing in, say, the orthorhombic system (e.g. aragonite) may, by twinning, give rise to pseudo-hexagonal forms: and pseudo-cubic forms often result by the complex twinning of crystals (e.g. stannite, phillipsite, &c.) belonging to other systems. Many of the so-called “optical anomalies” of crystals may be explained by this pseudo-symmetric twinning.
(h) Irregularities of Growth of Crystals; Character of Faces.
Only rarely do actual crystals present the symmetrical appearance shown in the figures given above, in which similar faces are all represented as of equal size. It frequently happens that the crystal is so placed with respect to the liquid in which it grows that there will be a more rapid deposition of material on one part than on another; for instance, if the crystal be attached to some other solid it cannot grow in that direction. Only when a crystal is freely suspended in the mother-liquid and material for growth is supplied at the same rate on all sides does an equably developed form result.
 | |
| Fig. 85. | Fig. 86. |
| Misshappen Octahedra. | |
Two misshapen or distorted octahedra are represented in figs. 85 and 86; the former is elongated in the direction of one of the edges of the octahedron, and the latter is flattened parallel to one pair of faces. It will be noticed in these figures that the edges in which the faces intersect have the same directions as before, though here there are additional edges not present in fig. 3. The angles (70° 32′ or 109° 28′) between the faces also remain the same; and the faces have the same inclinations to the axes and planes of symmetry as in the equably developed form. Although from a geometrical point of view these figures are no longer symmetrical with respect to the axes and planes of symmetry, yet crystallographically they are just as symmetrical as the ideally developed form, and, however much their irregularity of development, they still are regular (cubic) octahedra of crystallography. A remarkable case of irregular development is presented by the mineral cuprite, which is often found as well-developed octahedra; but in the variety known as chalcotrichite it occurs as a matted aggregate of delicate hairs, each of which is an individual crystal enormously elongated in the direction of an edge or diagonal of the cube.
The symmetry of actual crystals is sometimes so obscured by irregularities of growth that it can only be determined by measurement of the angles. An extreme case, where several of the planes have not been developed at all, is illustrated in fig. 87, which shows the actual shape of a crystal of zircon from Ceylon; the ideally developed form (fig. 88) is placed at the side for comparison, and the parallelism of the edges between corresponding faces will be noticed. This crystal is a combination of five simple forms, viz. two tetragonal prisms (a and m,) two tetragonal bipyramids (e and p), and one ditetragonal bipyramid (x, with 16 faces).
 | |
| Fig. 87.—Actual Crystal. | Fig. 88.—Ideal Development. |
| Crystal of Zircon (clinographic drawings and plans). | |
The actual form, or “habit,” of crystals may vary widely in different crystals of the same substance, these differences depending largely on the conditions under which the growth has taken place. The material may have crystallized from a fused mass or from a solution; and in the latter case the solvent may be of different kinds and contain other substances in solution, or the temperature may vary. Calcite (q.v.) affords a good example of a substance crystallizing in widely different habits, but all crystals are referable to the same type of symmetry and may be reduced to the same fundamental form.
When crystals are aggregated together, and so interfere with each other’s growth, special structures and external shapes often result, which are sometimes characteristic of certain substances, especially amongst minerals.
Incipient crystals, the development of which has been arrested owing to unfavourable conditions of growth, are known as crystallites (q.v.). They are met with in imperfectly crystallized substances and in glassy rocks (obsidian and pitchstone), or may be obtained artificially from a solution of sulphur in carbon disulphide rendered viscous by the addition of Canada-balsam. To the various forms H. Vogelsang gave, in 1875, the names “globulites,” “margarites” (from μαργαρίτης, a pearl), “longulites,” &c. At a more advanced stage of growth these bodies react on polarized light, thus possessing the internal structure of true crystals; they are then called “microlites.” These have the form of minute rods, needles or hairs, and are aggregated into feathery and spherulitic forms or skeletal crystals. They are common constituents of microcrystalline igneous rocks, and often occur as inclusions in larger crystals of other substances.
Inclusions of foreign matter, accidentally caught up during growth, are frequently present in crystals. Inclusions of other minerals are specially frequent and conspicuous in crystals of quartz, and crystals of calcite may contain as much as 60% of included sand. Cavities, either with rounded boundaries or with the same shape (“negative crystals”) as the surrounding crystal, are often to be seen; they may be empty or enclose a liquid with a movable bubble of gas.
The faces of crystals are rarely perfectly plane and smooth, but are usually striated, studded with small angular elevations, pitted or cavernous, and sometimes curved or twisted. These irregularities, however, conform with the symmetry of the crystal, and much may be learnt by their study. The parallel grooves or furrows, called “striae,” are the result of oscillatory combination between adjacent faces, narrow strips of first one face and then another being alternately developed. Sometimes the striae on crystal-faces are due to repeated lamellar twinning, as in the plagioclase felspars. The directions of the striations are very characteristic features of many crystals: e.g. the faces of the hexagonal prism of quartz are always striated horizontally, whilst in beryl they are striated vertically. Cubes of pyrites (fig. 89) are striated parallel to one edge, the striae on adjacent faces being at right angles, and due to oscillatory combination of the cube and the pentagonal dodecahedron (compare fig. 36); whilst cubes of blende (fig. 90) are striated parallel to one diagonal of each face, i.e. parallel to the tetrahedron faces (compare fig. 31). These striated cubes thus possess different degrees of symmetry and belong to different symmetry-classes. Oscillatory combination of faces gives rise also to curved surfaces. Crystals with twisted surfaces (see Dolomite) are, however, built up of smaller crystals arranged in nearly parallel position. Sometimes a face is entirely replaced by small faces of other forms, giving rise to a drusy surface; an example of this is shown by some octahedral crystals of fluorspar (fig. 2) which are built up of minute cubes.
 | |
| Fig. 89.—Striated Cube of Pyrites. |
Fig. 90.—Striated Cube of Blende. |
The faces of crystals are sometimes partly or completely replaced by smooth bright surfaces inclined at only a few minutes of arc from the true position of the face; such surfaces are called “vicinal faces,” and their indices can be expressed only by very high numbers. In apparently perfectly developed crystals of alum the octahedral face, with the simple indices (111), is usually replaced by faces of very low triakis-octahedra, with indices such as (251·251·250); the angles measured on such crystals will therefore deviate slightly from the true octahedral angle. Vicinal faces of this character are formed during the growth of crystals, and have been studied by H. A. Miers (Phil. Trans., 1903, Ser. A. vol. 202). Other faces with high indices, viz. “prerosion faces” and the minute faces forming the sides of etched figures (see below), as well as rounded edges and other surface irregularities, may, however, result from the corrosion of a crystal subsequent to its growth. The pitted and cavernous faces of artificially grown crystals of sodium chloride and of bismuth are, on the other hand, a result of rapid growth, more material being supplied at the edges and corners of the crystal than at the centres of the faces.
(i) Theories of Crystal Structure.
The ultimate aim of crystallographic research is to determine the internal structure of crystals from both physical and chemical data. The problem is essentially twofold: in the first place it is necessary to formulate a theory as to the disposition of the molecules, which conforms with the observed types of symmetry—this is really a mathematical problem; in the second place, it is necessary to determine the orientation of the atoms (or groups of atoms) composing the molecules with regard to the crystal axes—this involves a knowledge of the atomic structure of the molecule. As appendages to the second part of our problem, there have to be considered: (1) the possibility of the existence of the same substance in two or more distinct crystalline forms—polymorphism, and (2) the relations between the chemical structure of compounds which affect nearly identical or related crystal habits—isomorphism and morphotropy. Here we shall discuss the modern theory of crystal structure; the relations between chemical composition and crystallographical form are discussed in Part III. of this article; reference should also be made to the article Chemistry: Physical.
The earliest theory of crystal structure of any moment is that of Haüy, in which, as explained above, he conceived a crystal as composed of elements bounded by the cleavage planes of the crystal, the elements being arranged contiguously and along parallel lines. There is, however, no Haüy. reason to suppose that matter is continuous throughout a crystalline body; in fact, it has been shown that space does separate the molecules, and we may therefore replace the contiguous elements of Haüy by particles equidistantly distributed along parallel lines; by this artifice we retain the reticulated or net-like structure, but avoid the continuity of matter which characterizes Haüy’s theory; the permanence of crystal form being due to equilibrium between the intermolecular (and interatomic) forces. The crystal is thus conjectured as a “space-lattice,” composed of three sets of parallel planes which enclose parallelopipeda, at the corners of which are placed the constituent molecules (or groups of molecules) of the crystal.
The geometrical theory of crystal structure (i.e. the determination of the varieties of crystal symmetry) is thus reduced to the mathematical problem: “in how many ways can space be partitioned?” M. L. Frankenheim, in 1835, determined this number as fifteen, but A. Bravais, Franken-heim; Bravais. in 1850, proved the identity of two of Frankenheim’s forms, and showed how the remaining fourteen coalesced by pairs, so that really these forms only corresponded to seven distinct systems and fourteen classes of crystal symmetry. These systems, however, only represented holohedral forms, leaving the hemihedral and tetartohedral classes to be explained. Bravais attempted an explanation by attributing differences in the symmetry of the crystal elements, or, what comes to the same thing, he assumed the crystals to exhibit polar differences along any member of the lattice; for instance, assume the particles to be (say) pear-shaped, then the sharp ends point in one direction, the blunt ends in the opposite direction.
A different view was adopted by L. Sohncke in 1879, who, by developing certain considerations published by Camille Jordan in 1869 on the possible types of regular repetition in space of identical parts, showed that the lattice-structure of Bravais was unnecessary, it being sufficient Sohncke. that each molecule of an indefinitely extended crystal, represented by its “point” (or centre of gravity), was identically situated with respect to the molecules surrounding it. The problem then resolves itself into the determination of the number of “point-systems” possible; Sohncke derived sixty-five such arrangements, which may also be obtained from the fourteen space-lattices of Bravais, by interpenetrating any one space-lattice with one or more identical lattices, with the condition that the resulting structure should conform with the homogeneity characteristic of crystals. But the sixty-five arrangements derived by Sohncke, of which Bravais’ lattices are particular cases, did not complete the solution, for certain of the known types of crystal symmetry still remained unrepresented. These missing forms are characterized as being enantiomorphs consequently, with the introduction of this principle of repetition over a plane, i.e. mirror images. E. S. Fedorov (1890), A. Schoenflies (1891), and W. Barlow (1894), independently and by different methods, showed how Sohncke’s theory of regular point-systems explained the whole thirty-two classes of crystal symmetry, 230 distinct types of crystal structure falling into these classes.
By considering the atoms instead of the centres of gravity of the molecules, Sohncke (Zeits. Kryst. Min., 1888, 14, p. 431) has generalized his theory, and propounded the structure of a crystal in the following terms: “A crystal consists of a finite number of interpenetrating regular point-systems, which all possess like and like-directed coincidence movements. Each separate point-system is occupied by similar material particles, but these may be different for the different interpenetrating partial systems which form the complex system.” Or we may quote the words of P. von Groth (British Assoc. Rep., 1904): “A crystal—considered as indefinitely extended—consists of n interpenetrating regular point-systems, each of which is formed of similar atoms; each of these point-systems is built up from a number of interpenetrating space-lattices, each of the latter being formed from similar atoms occupying parallel positions. All the space-lattices of the combined system are geometrically identical, or are characterized by the same elementary parallelopipedon.”
A complete résumé, with references to the literature, will be found in “Report on the Development of the Geometrical Theories of Crystal Structure, 1666–1901” (British Assoc. Rep., 1901).
II. PHYSICAL PROPERTIES OF CRYSTALS.
Many of the physical properties of crystals vary with the direction in the material, but are the same in certain directions; these directions obeying the same laws of symmetry as do the faces on the exterior of the crystal. The symmetry of the internal structure of crystals is thus the same as the symmetry of their external form.
(a) Elasticity and Cohesion.
The elastic constants of crystals are determined by similar methods to those employed with amorphous substances, only the bars and plates experimented upon must be cut from the crystal with known orientations. The “elasticity surface” expressing the coefficients in various directions within the crystal has a configuration symmetrical with respect to the same planes and axes of symmetry as the crystal itself. In calcite, for instance, the figure has roughly the shape of a rounded rhombohedron with depressed faces and is symmetrical about three vertical planes. In the case of homogeneous elastic deformation, produced by pressure on all sides, the effect on the crystal is the same as that due to changes of temperature; and the surfaces expressing the compression coefficients in different directions have the same higher degree of symmetry, being either a sphere, spheroid or ellipsoid. When strained beyond the limits of elasticity, crystalline matter may suffer permanent deformation in one or other of two ways, or may be broken along cleavage surfaces or with an irregular fracture. In the case of plastic deformation, e.g. in a crystal of ice, the crystalline particles are displaced but without any change in their orientation. Crystals of some substances (e.g. para-azoxyanisol) have such a high degree of plasticity that they are deformed even by their surface tension, and the crystals take the form of drops of doubly refracting liquid which are known as “liquid crystals.” (See O. Lehmann, Flüssige Kristalle, Leipzig, 1904; F. R. Schenck, Kristallinische Flüssigkeiten und flüssige Krystalle, Leipzig, 1905.)
 |
| Fig. 91.—Glide-plane of Calcite. |
In the second, and more usual kind of permanent deformation without fracture, the particles glide along certain planes into a new (twinned) position of equilibrium. If a knife blade be pressed into the edge of a cleavage rhombohedron of calcite (at b, fig. 91) the portion abcde of the crystal will take up the position a′b′cde. The obtuse solid angle at a becomes acute (a′), whilst the acute angle at b becomes obtuse (b′); and the new surface a′ce is as bright and smooth as before. This result has been effected by the particles in successive layers gliding or rotating over each other, without separation, along planes parallel to cde. This plane, which truncates the edge of the rhombohedron and has the indices (110), is called a “glide-plane.” The new portion is in twinned position with respect to the rest of the crystal, being a reflection of it across the plane cde, which is therefore a plane of twinning. This secondary twinning is often to be observed as a repeated lamination in the grains of calcite composing a crystalline limestone, or marble, which has been subjected to earth movements. Planes of gliding have been observed in many minerals (pyroxene, corundum, &c.) and their crystals may often be readily broken along these directions, which are thus “planes of parting” or “pseudo-cleavage.” The characteristic transverse striae, invariably present on the cleavage surfaces of stibnite and cyanite are due to secondary twinning along glide-planes, and have resulted from the bending of the crystals.
One of the most important characters of crystals is that of “cleavage”; there being certain plane directions across which the cohesion is a minimum, and along which the crystal may be readily split or cleaved. These directions are always parallel to a possible face on the crystal and usually one prominently developed and with simple indices, it being a face in which the crystal molecules are most closely packed. The directions of cleavage are symmetrically repeated according to the degree of symmetry possessed by the crystal. Thus in the cubic system, crystals of salt and galena cleave in three directions parallel to the faces of the cube {100}, diamond and fluorspar cleave in four directions parallel to the octahedral faces {111}, and blende in six directions parallel to the faces of the rhombic dodecahedron {110}. In crystals of other systems there will be only a single direction of cleavage if this is parallel to the faces of a pinacoid; e.g. the basal pinacoid in tetragonal (as in apophyllite) and hexagonal crystals; or parallel (as in gypsum) or perpendicular (as in mica and cane-sugar) to the plane of symmetry in monoclinic crystals. Calcite cleaves in three directions parallel to the faces of the primitive rhombohedron. Barytes, which crystallizes in the orthorhombic system, has two sets of cleavages, viz. a single cleavage parallel to the basal pinacoid {001} and also two directions parallel to the faces of the prism {110}. In all of the examples just quoted the cleavage is described as perfect, since cleavage flakes with very smooth and bright surfaces may be readily detached from the crystals. Different substances, however, vary widely in their character of cleavage; in some it can only be described as good or distinct, whilst in others, e.g. quartz and alum, there is little or no tendency to split along certain directions and the surfaces of fracture are very uneven. Cleavage is therefore a character of considerable determinative value, especially for the purpose of distinguishing different minerals.
Another result of the presence in crystals of directions of minimum cohesion are the “percussion figures,” which are produced on a crystal-face when this is struck with a sharp point. A percussion figure consists of linear cracks radiating from the point of impact, which in their number and orientation agree with the symmetry of the face. Thus on a cube face of a crystal of salt the rays of the percussion figure are parallel to the diagonals of the face, whilst on an octahedral face a three-rayed star is developed. By pressing a blunt point into a crystal face a somewhat similar figure, known as a “pressure figure,” is produced. Percussion and pressure figures are readily developed in cleavage sheets of mica (q.v.).
Closely allied to cohesion is the character of “hardness,” which is often defined, and measured by, the resistance which a crystal face offers to scratching. That hardness is a character depending largely on crystalline structure is well illustrated by the two crystalline modifications of carbon: graphite is one of the softest of minerals, whilst diamond is the hardest of all. The hardness of crystals of different substances thus varies widely, and with minerals it is a character of considerable determinative value; for this purpose a scale of hardness is employed (see Mineralogy). Various attempts have been made with the view of obtaining accurate determinations of degrees of hardness, but with varying results; an instrument used for this purpose is called a sclerometer (from σκληρός, hard). It may, however, be readily demonstrated that the degree of hardness on a crystal face varies with the direction, and that a curve expressing these relations possesses the same geometrical symmetry as the face itself. The mineral cyanite is remarkable in having widely different degrees of hardness on different faces of its crystals and in different directions on the same face.
Another result of the differences of cohesion in different directions is that crystals are corroded, or acted upon by chemical solvents, at different rates in different directions. This is strikingly shown when a sphere cut from a crystal, say of calcite or quartz, is immersed in acid; after some time the resulting form is bounded by surfaces approximating to crystal faces, and has the same symmetry as that of the crystal from which the sphere was cut. When a crystal bounded by faces is immersed in a solvent the edges and corners become rounded and “prerosion faces” developed in their place; the faces become marked all over with minute pits or shallow depressions, and as these are extended by further solution they give place to small elevations on the corroded face. The sides of the pits and elevations are bounded by small faces which have the character of vicinal faces. These markings are known as “etched figures” or “corrosion figures,” and they are extremely important aids in determining the symmetry of crystals. Etched figures are sometimes beautifully developed on the faces of natural crystals, e.g. of diamond, and they may be readily produced artificially with suitable solvents.
 | ||
| Fig. 92.—Nepheline. | Fig. 93.—Calcite. | Fig. 94.—Beryl. |
| Etched Figures on Hexagonal Prisms. | ||
As an example, the etched figures on the faces of a hexagonal prism and the basal plane are illustrated in figs. 92-94 for three of the several symmetry-classes of the hexagonal system. The classes chosen are those in which nepheline, calcite and beryl (emerald) crystallize, and these minerals often have the simple form of crystal represented in the figures. In nepheline (fig. 92) the only element of symmetry is a hexad axis; the etched figures on the prism are therefore unsymmetrical, though similar on all the faces; the hexagonal markings on the basal plane have none of their edges parallel to the edges of the face; further the crystals being hemimorphic, the etched figures on the basal planes at the two ends will be different in character. The facial development of crystals of nepheline give no indication of this type of symmetry, and the mineral has been referred to this class solely on the evidence afforded by the etched figures. In calcite there is a triad axis of symmetry parallel to the prism edges, three dyad axes each perpendicular to a pair of prism edges and three planes of symmetry perpendicular to the prism faces; the etched figures shown in fig. 93 will be seen to conform to all these elements of symmetry. There being in calcite also a centre of symmetry, the equilateral triangles on the basal plane at the lower end of the crystal will be the same in form as those at the top, but they will occupy a reversed position. In beryl, which crystallizes in the holosymmetric class of the hexagonal system, the etched figures (fig. 94) display the fullest possible degree of symmetry; those on the prism faces are all similar and are each symmetrical with respect to two lines, and the hexagonal markings on the basal planes at both ends of the crystal are symmetrically placed with respect to six lines. A detailed account of the etched figures of crystals is given by H. Baumhauer, Die Resultate der Ätzmethode in der krystallographischen Forschung (Leipzig, 1894).
(b) Optical Properties.
The complex optical characters of crystals are not only of considerable interest theoretically, but are of the greatest practical importance. In the absence of external crystalline form, as with a faceted gem-stone, or with the minerals constituting a rock (thin, transparent sections of which are examined in the polarizing microscope), the mineral species may often be readily identified by the determination of some of the optical characters.
According to their action on transmitted plane-polarized light (see Polarization of Light) all crystals may be referred to one or other of the five groups enumerated below. These groups correspond with the six systems of crystallization (in the second group two systems being included together). The several symmetry-classes of each system are optically the same, except in the rare cases of substances which are circularly polarizing.
(1) Optically isotropic crystals—corresponding with the cubic system.
(2) Optically uniaxial crystals—corresponding with the tetragonal and hexagonal systems.
(3) Optically biaxial crystals in which the three principal optical directions coincide with the three crystallographic axes—corresponding with the orthorhombic system.
(4) Optically biaxial crystals in which only one of the three principal optical directions coincides with a crystallographic axis—corresponding with the monoclinic system.
(5) Optically biaxial crystals in which there is no fixed and definite relation between the optical and crystallographic directions—corresponding with the anorthic system.
Optically Isotropic Crystals.—These belong to the cubic system, and like all other optically isotropic (from ἴσος, like, and τρόπος, character) bodies have only one index of refraction for light of each colour. They have no action on polarized light (except in crystals which are circularly polarizing); and when examined in the polariscope or polarizing microscope they remain dark between crossed nicols, and cannot therefore be distinguished optically from amorphous substances, such as glass and opal.
Optically Uniaxial Crystals.—These belong to the tetragonal and hexagonal (including rhombohedral) systems, and between crystals of these systems there is no optical distinction. Such crystals are anisotropic or doubly refracting (see Refraction: Double); but for light travelling through them in a certain, single direction they are singly refracting. This direction, which is called the optic axis, is the same for light of all colours and at all temperatures; it coincides in direction with the principal crystallographic axis, which in tetragonal crystals is a tetrad (or dyad) axis of symmetry, and in the hexagonal system a triad or hexad axis.
For light of each colour there are two indices of refraction; namely, the ordinary index (ω) corresponding with the ordinary ray, which vibrates perpendicular to the optic axis; and the extraordinary index (ε) corresponding with the extraordinary ray, which vibrates parallel to the optic axis. If the ordinary index of refraction be greater than the extraordinary index, the crystal is said to be optically negative, whilst if less the crystal is optically positive. The difference between the two indices is a measure of the strength of the double refraction or birefringence. Thus in calcite, for sodium (D) light, ω = 1.6585 and ε = 1.4863; hence this substance is optically negative with a relatively high double refraction of ω − ε = 0.1722. In quartz ω = 1.5442, ε = 1.5533 and ε − ω = 0.0091; this mineral is therefore optically positive with low double refraction. The indices of refraction vary, not only for light of different colours, but also slightly with the temperature.
The optical characters of uniaxial crystals are symmetrical not only with respect to the full number of planes and axes of symmetry of tetragonal and hexagonal crystals, but also with respect to all vertical planes, i.e. all planes containing the optic axis. A surface expressing the optical relations of such crystals is thus an ellipsoid of revolution about the optic axis. (In cubic crystals the corresponding surface is a sphere.) In the “optical indicatrix” (L. Fletcher, The Optical Indicatrix and the Transmission of Light in Crystals, London, 1892), the length of the principal axis, or axis of rotation, is proportional to the index of refraction, (i.e. inversely proportional to the velocity) of the extraordinary rays, which vibrate along this axis and are transmitted in directions perpendicular thereto; the equatorial diameters are proportional to the index of refraction of the ordinary rays, which vibrate perpendicular to the optic axis. For positive uniaxial crystals the indicatrix is thus a prolate spheroid (egg-shaped), and for negative crystals an oblate spheroid (orange-shaped).
In “Fresnel’s ellipsoid” the axis of rotation is proportional to the velocity of the extraordinary ray, and the equatorial diameters proportional to the velocity of the ordinary ray; it is therefore an oblate spheroid for positive crystals, and a prolate spheroid for negative crystals. The “ray-surface,” or “wave-surface,” which represents the distances traversed by the rays during a given interval of time in various directions from a point of origin within the crystal, consists in uniaxial crystals of two sheets; namely, a sphere, corresponding to the ordinary rays, and an ellipsoid of revolution, corresponding to the extraordinary rays. The difference in form of the ray-surface for positive and negative crystals is shown in figs. 95 and 96.
 | |
| Fig. 95.—Section of the Ray-Surface of a Positive Uniaxial Crystal. |
Fig. 96.—Section of the Ray-Surface of a Negative Uniaxial Crystal. |
When a uniaxial crystal is examined in a polariscope or polarizing microscope between crossed nicols (i.e. with the principal planes of the polarizer or analyser at right angles, and so producing a dark field of view) its behaviour differs according to the direction in which the light travels through the crystal, to the position of the crystal with respect to the principal planes of the nicols, and further, whether convergent or parallel polarized light be employed. A tetragonal or hexagonal crystal viewed, in parallel light, through the basal plane, i.e. along the principal axis, will remain dark as it is rotated between crossed nicols, and will thus not differ in its behaviour from a cubic crystal or other isotropic body. If, however, the crystal be viewed in any other direction, for example, through a prism face, it will, except in certain positions, have an action on the polarized light. A plane-polarized ray entering the crystal will be resolved into two polarized rays with the directions of vibration parallel to the vibration-directions in the crystal. These two rays on leaving the crystal will be combined again in the analyser, and a portion of the light transmitted through the instrument; the crystal will then show up brightly against the dark field. Further, owing to interference of these two rays in the analyser, the light will be brilliantly coloured, especially if the crystal be thin, or if a thin section of a crystal be examined. The particular colour seen will depend on the strength of the double refraction, the orientation of the crystal or section, and upon its thickness. If now, the crystal be rotated with the stage of the microscope, the nicols remaining fixed in position, the light transmitted through the instrument will vary in intensity, and in certain positions will be cut out altogether. The latter happens when the vibration-directions of the crystal are parallel to the vibration-directions of the nicols (these being indicated by cross-wires in the microscope). The crystal, now being dark, is said to be in position of extinction; and as it is turned through a complete rotation of 360° it will extinguish four times. If a prism face be viewed through, it will be seen that, when the crystal is in a position of extinction, the cross-wires of the microscope are parallel to the edges of the prism: the crystal is then said to give “straight extinction.”
 |
| Fig. 97.—Interference Figure of a Uniaxial Crystal. |
In convergent light, between crossed nicols, a very different phenomenon is to be observed when a uniaxial crystal, or section of such a crystal, is placed with its optic axis coincident with the axis of the microscope. The rays of light, being convergent, do not travel in the direction of the optic axis and are therefore doubly refracted in the crystal; in the analyser the vibrations will be reduced to the same plane and there will be interference of the two sets of rays. The result is an “interference figure” (fig. 97), which consists of a number of brilliantly coloured concentric rings, each showing the colours of the spectrum of white light; intersecting the rings is a black cross, the arms of which are parallel to the principal planes of the nicols. If monochromatic light be used instead of white light, the rings will be alternately light and dark. The number and distance apart of the rings depend on the strength of the double refraction and on the thickness of the crystal. By observing the effect produced on such a uniaxial interference figure when a “quarter undulation (or wave-length) mica-plate” is superposed on the crystal, it may be at once decided whether the crystal is optically positive or negative. Such a simple test may, for example, be applied for distinguishing certain faceted gem-stones: thus zircon and phenacite are optically positive, whilst corundum (ruby and sapphire) and beryl (emerald) are optically negative.
Optically Biaxial Crystals.—In these crystals there are three principal indices of refraction, denoted by α, β and γ; of these γ is the greatest and α the least (γ > β > α). The three principal vibration-directions, corresponding to these indices, are at right angles to each other, and are the directions of the three rectangular axes of the optical indicatrix. The indicatrix (fig. 98) is an ellipsoid with the lengths of its axes proportional to the refractive indices; OC = γ, OB = β, OA = α, where OC > OB > OA. The figure is symmetrical with respect to the principal planes OAB, OAC, OBC.
In Fresnel’s ellipsoid the three rectangular axes are proportional to 1/α, 1/β, and 1/γ, and are usually denoted by a, b and c respectively, where a > b > c: these have often been called “axes of optical elasticity,” a term now generally discarded.
 | |
| Fig. 98.—Optical Indicatrix of a Biaxial Crystal. |
Fig. 99.—Ray-Surface of a Biaxial Crystal. |
The ray-surface (represented in fig. 99 by its sections in the three principal planes) is derived from the indicatrix in the following manner. A ray of light entering the crystal and travelling in the direction OA is resolved into polarized rays vibrating parallel to OB and OC, and therefore propagated with the velocities 1/β and 1/γ respectively: distances Ob and Oc (fig. 99) proportional to these velocities are marked off in the direction OA. Similarly, rays travelling along OC have the velocities 1/α and 1/β, and those along OB the velocities 1/α and 1/γ. In the two directions Op1 and Op2 (fig. 98), perpendicular to the two circular sections P1P1 and P2P2 of the indicatrix, the two rays will be transmitted with the same velocity 1/β. These two directions are called the optic axes (“primary optic axis”), though they have not all the properties which are associated with the optic axis of a uniaxial crystal. They have very nearly the same direction as the lines Os1 and Os2 in fig. 99, which are distinguished as the “secondary optic axes.” In most crystals the primary and secondary optic axes are inclined to each other at not more than a few minutes, so that for practical purposes there is no distinction between them.
The angle between Op1 and Op2 is called the “optic axial angle”; and the plane OAC in which they lie is called the “optic axial plane.” The angles between the optic axes are bisected by the vibration-directions OA and OC; the one which bisects the acute angle being called the “acute bisectrix” or “first mean line,” and the other the “obtuse bisectrix” or “second mean line.” When the acute bisectrix coincides with the greatest axis OC of the indicatrix, i.e. the vibration-direction corresponding with the refractive index γ (as in figs. 98 and 99), the crystal is described as being optically positive; and when the acute bisectrix coincides with OA, the vibration-direction for the index α, the crystal is negative. The distinction between positive and negative biaxial crystals thus depends on the relative magnitude of the three principal indices of refraction; in positive crystals β is nearer to α than to γ, whilst in negative crystals the reverse is the case. Thus in topaz, which is optically positive, the refractive indices for sodium light are α = 1.6120, β = 1.6150, γ = 1.6224; and for orthoclase which is optically negative, α = 1.5190, β = 1.5237, γ = 1.5260. The difference γ − α represents the strength of the double refraction.
Since the refractive indices vary both with the colour of the light and with the temperature, there will be for each colour and temperature slight differences in the form of both the indicatrix and the ray-surface: consequently there will be variations in the positions of the optic axes and in the size of the optic axial angle. This phenomenon is known as the “dispersion of the optic axes.” When the axial angle is greater for red light than for blue the character of the dispersion is expressed by ρ > υ, and when less by ρ < υ. In some crystals, e.g. brookite, the optic axes for red light and for blue light may be, at certain temperatures, in planes at right angles.
 | |
| Fig. 100. | Fig. 101. |
| Interference Figures of a Biaxial Crystal. | |
The type of interference figure exhibited by a biaxial crystal in convergent polarized light between crossed nicols is represented in figs. 100 and 101. The crystal must be viewed along the acute bisectrix, and for this purpose it is often necessary to cut a plate from the crystal perpendicular to this direction: sometimes, however, as in mica and topaz, a cleavage flake will be perpendicular to the acute bisectrix. When seen in white light, there are around each optic axis a series of brilliantly coloured ovals, which at the centre join to form an 8-shaped loop, whilst further from the centre the curvature of the rings is approximately that of lemniscates. In the position shown in fig. 100 the vibration-directions in the crystal are parallel to those of the nicols, and the figure is intersected by two black bands or “brushes” forming a cross. When, however, the crystal is rotated with the stage of the microscope the cross breaks up into the two branches of a hyperbola, and when the vibration-directions of the crystal are inclined at 45° to those of the nicols the figure is that shown in fig. 101. The points of emergence of the optic axes are at the middle of the hyperbolic brushes when the crystal is in the diagonal position: the size of the optic axial angle can therefore be directly measured with considerable accuracy.
In orthorhombic crystals the three principal vibration-directions coincide with the three crystallographic axes, and have therefore fixed positions in the crystal, which are the same for light of all colours and at all temperatures. The optical orientation of an orthorhombic crystal is completely defined by stating to which crystallographic planes the optic axial plane and the acute bisectrix are respectively parallel and perpendicular. Examined in parallel light between crossed nicols, such a crystal extinguishes parallel to the crystallographic axes, which are often parallel to the edges of a face or section; there is thus usually “straight extinction.” The interference figure seen in convergent polarized light is symmetrical about two lines at right angles.
In monoclinic crystals only one vibration-direction has a fixed position within the crystal, being parallel to the ortho-axis (i.e. perpendicular to the plane of symmetry or the plane (010)). The other two vibration-directions lie in the plane (010), but they may vary in position for light of different colours and at different temperatures. In addition to dispersion of the optic axes there may thus, in crystals of this system, be also “dispersion of the bisectrices.” The latter may be of one or other of three kinds, according to which of the three vibration-directions coincides with the ortho-axis of the crystal. When the acute bisectrix is fixed in position, the optic axial planes for different colours may be crossed, and the interference figure will then be symmetrical with respect to a point only (“crossed dispersion”). When the obtuse bisectrix is fixed, the axial planes may be inclined to one another, and the interference figure is symmetrical only about a line which is perpendicular to the axial planes (“horizontal dispersion”). Finally, when the vibration-direction corresponding to the refractive index β, or the “third mean line,” has a fixed position, the optic axial plane lies in the plane (010), but the acute bisectrix may vary in position in this plane; the interference figure will then be symmetrical only about a line joining the optic axes (“inclined dispersion”). Examples of substances exhibiting these three kinds of dispersion are borax, orthoclase and gypsum respectively. In orthoclase and gypsum, however, the optic axial angle gradually diminishes as the crystals are heated, and after passing through a uniaxial position they open out in a plane at right angles to the one they previously occupied; the character of the dispersion thus becomes reversed in the two examples quoted. When examined in parallel light between crossed nicols monoclinic crystals will give straight extinction only in faces and sections which are perpendicular to the plane of symmetry (or the plane (010)); in all other faces and sections the extinction-directions will be inclined to the edges of the crystal. The angles between these directions and edges are readily measured, and, being dependent on the optical orientation of the crystal, they are often characteristic constants of the substance (see, e.g., Plagioclase).
In anorthic crystals there is no relation between the optical and crystallographic directions, and the exact determination of the optical orientation is often a matter of considerable difficulty. The character of the dispersion of the bisectrices and optic axes is still more complex than in monoclinic crystals, and the interference figures are devoid of symmetry.
Absorption of Light in Crystals: Pleochroism.—In crystals other than those of the cubic system, rays of light with different vibration-directions will, as a rule, be differently absorbed; and the polarized rays on emerging from the crystal may be of different intensities and (if the observation be made in white light and the crystal is coloured) differently coloured. Thus, in tourmaline the ordinary ray, which vibrates perpendicular to the principal axis, is almost completely absorbed, whilst the extraordinary ray is allowed to pass through the crystal. A plate of tourmaline cut parallel to the principal axis may therefore be used for producing a beam of polarized light, and two such plates placed in crossed position form the polarizer or analyser of “tourmaline tongs,” with the aid of which the interference figures of crystals may be simply shown. Uniaxial (tetragonal and hexagonal) crystals when showing perceptible differences in colour for the ordinary and extraordinary rays are said to be “dichroic.” In biaxial (orthorhombic, monoclinic and anorthic) crystals, rays vibrating along each of the three principal vibration-directions may be differently absorbed, and, in coloured crystals, differently coloured; such crystals are therefore said to be “trichroic” or in general “pleochroic” (from πλέων, more, and χρόα, colour). The directions of maximum absorption in biaxial crystals have, however, no necessary relation with the axes of the indicatrix, unless these have fixed crystallographic directions, as in the orthorhombic system and the ortho-axis in the monoclinic. In epidote it has been shown that the two directions of maximum absorption which lie in the plane of symmetry are not even at right angles.
 |
| Fig. 102.—Dichroscope. |
The pleochroism of some crystals is so strong that when they are viewed through in different directions they exhibit marked differences in colour. Thus a crystal of the mineral iolite (called also dichroite because of its strong pleochroism) will be seen to be dark blue, pale blue or pale yellow according to which of three perpendicular directions it is viewed. The “face colours” seen directly in this way result, however, from the mixture of two “axial colours” belonging to rays vibrating in two directions. In order to see the axial colours separately the crystal must be examined with a dichroscope, or in a polarizing microscope from which the analyser has been removed. The dichroscope, or dichroiscope (fig. 102), consists of a cleavage rhombohedron of calcite (Iceland-spar) p, on the ends of which glass prisms w are cemented: the lens l is focused on a small square aperture o in the tube of the instrument. The eye of the observer placed at e will see two images of the square aperture, and if a pleochroic crystal be placed in front of this aperture the two images will be differently coloured. On rotating this crystal with respect to the instrument the maximum difference in the colours will be obtained when the vibration-directions in the crystal coincide with those in the calcite. Such a simple instrument is especially useful for the examination of faceted gem-stones, even when they are mounted in their settings. A single glance suffices to distinguish between a ruby and a “spinel-ruby,” since the former is dichroic and the latter isotropic and therefore not dichroic.
The characteristic absorption bands in the spectrum of white light which has been transmitted through certain crystals, particularly those of salts of the cerium metals, will, of course, be different according to the direction of vibration of the rays.
Circular Polarization in Crystals.—Like the solutions of certain optically active organic substances, such as sugar and tartaric acid, some optically isotropic and uniaxial crystals possess the property of rotating the plane of polarization of a beam of light. In uniaxial (tetragonal and hexagonal) crystals it is only for light transmitted in the direction of the optic axis that there is rotatory action, but in isotropic (cubic) crystals all directions are the same in this respect. Examples of circularly polarizing cubic crystals are sodium chlorate, sodium bromate, and sodium uranyl acetate; amongst tetragonal crystals are strychnine sulphate and guanidine carbonate; amongst rhombohedral are quartz (q.v.) and cinnabar (q.v.) (these being the only two mineral substances in which the phenomenon has been observed), dithionates of potassium, lead, calcium and strontium, and sodium periodate; and amongst hexagonal crystals is potassium lithium sulphate. Crystals of all these substances belong to one or other of the several symmetry-classes in which there are neither planes nor centre of symmetry, but only axes of symmetry. They crystallize in two complementary hemihedral forms, which are respectively right-handed and left-handed, i.e. enantiomorphous forms. Some other substances which crystallize in enantiomorphous forms are, however, only “optically active” when in solution (e.g. sugar and tartaric acid); and there are many other substances presenting this peculiarity of crystalline form which are not circularly polarizing either when crystallized or when in solution. Further, in the examples quoted above, the rotatory power is lost when the crystals are dissolved (except in the case of strychnine sulphate, which is only feebly active in solution). The rotatory power is thus due to different causes in the two cases, in the one depending on a spiral arrangement of the crystal particles, and in the other on the structure of the molecules themselves.
The circular polarization of crystals may be imitated by a pile of mica plates, each plate being turned through a small angle on the one below, thus giving a spiral arrangement to the pile.
“Optical Anomalies” of Crystals.—When, in 1818, Sir David Brewster established the important relations existing between the optical properties of crystals and their external form, he at the same time noticed many apparent exceptions. For example, he observed that crystals of leucite and boracite, which are cubic in external form, are always doubly refracting and optically biaxial, but with a complex internal structure; and that cubic crystals of garnet and analcite sometimes exhibit the same phenomena. Also some tetragonal and hexagonal crystals, e.g. apophyllite, vesuvianite, beryl, &c., which should normally be optically uniaxial, sometimes consist of several biaxial portions arranged in sectors or in a quite irregular manner. Such exceptions to the general rule have given rise to much discussion. They have often been considered to be due to internal strains in the crystals, set up as a result of cooling or by earth pressures, since similar phenomena are observed in chilled and compressed glasses and in dried gelatine. In many cases, however, as shown by E. Mallard, in 1876, the higher degree of symmetry exhibited by the external form of the crystals is the result of mimetic twinning, as in the pseudo-cubic crystals of leucite (q.v.) and boracite (q.v.). In other instances, substances not usually regarded as cubic, e.g. the monoclinic phillipsite (q.v.), may by repeated twinning give rise to pseudo-cubic forms. In some cases it is probable that the substance originally crystallized in one modification at a higher temperature, and when the temperature fell it became transformed into a dimorphous modification, though still preserving the external form of the original crystal (see Boracite). A summary of the literature is given by R. Brauns, Die optischen Anomalien der Krystalle (Leipzig, 1891).
(c) Thermal Properties.
 |
| Fig. 103.—Conductivity of Heat in Quartz. |
The thermal properties of crystals present certain points in common with the optical properties. Heat rays are transmitted and doubly refracted like light rays; and surfaces expressing the conductivity and dilatation in different directions possess the same degree of symmetry and are related in the same way to the crystallographic axes as the ellipsoids expressing the optical relations. That crystals conduct heat at different rates in different directions is well illustrated by the following experiment. Two plates (fig. 103) cut from a crystal of quartz, one parallel to the principal axis and the other perpendicular to it, are coated with a thin layer of wax, and a hot wire is applied to a point on the surface. On the transverse section the wax will be melted in a circle, and on the longitudinal section (or on the natural prism faces) in an ellipse. The isothermal surface in a uniaxial crystal is therefore a spheroid; in cubic crystals it is a sphere; and in biaxial crystals an ellipsoid, the three axes of which coincide, in orthorhombic crystals, with the crystallographic axes.
With change of temperature cubic crystals expand equally in all directions, and the angles between the faces are the same at all temperatures. In uniaxial crystals there are two principal coefficients of expansion; the one measured in the direction of the principal axis may be either greater or less than that measured in directions perpendicular to this axis. A sphere cut from a uniaxial crystal at one temperature will be a spheroid at another temperature. In biaxial crystals there are different coefficients of expansion along three rectangular axes, and a sphere at one temperature will be an ellipsoid at another. A result of this is that for all crystals, except those belonging to the cubic system, the angles between the faces will vary, though only slightly, with changes of temperature. E. Mitscherlich found that the rhombohedral angle of calcite decreases 8′ 37″ as the crystal is raised in temperature from 0° to 100° C.
As already mentioned, the optical properties of crystals vary considerably with the temperature. Such characters as specific heat and melting-point, which do not vary with the direction, are the same in crystals as in amorphous substances.
(d ) Magnetic and Electrical Properties.
Crystals, like other bodies, are either paramagnetic or diamagnetic, i.e. they are either attracted or repelled by the pole of a magnet. In crystals other than those belonging to the cubic system, however, the relative strength of the induced magnetization is different in different directions within the mass. A sphere cut from a tetragonal or hexagonal (uniaxial) crystal will if freely suspended in a magnetic field (between the poles of a strong electro-magnet) take up a position such that the principal axis of the crystal is either parallel or perpendicular to the lines of force, or to a line joining the two poles of the magnet. Which of these two directions is taken by the axis depends on whether the crystal is paramagnetic or diamagnetic, and on whether the principal axis is the direction of maximum or minimum magnetization. The surface expressing the magnetic character in different directions is in uniaxial crystals a spheroid; in cubic crystals it is a sphere. In orthorhombic, monoclinic and anorthic crystals there are three principal axes of magnetic induction, and the surface is an ellipsoid, which is related to the symmetry of the crystal in the same way as the ellipsoids expressing the thermal and optical properties.
Similarly, the dielectric constants of a non-conducting crystal may be expressed by a sphere, spheroid or ellipsoid. A sphere cut from a crystal will when suspended in an electro-magnetic field set itself so that the axis of maximum induction is parallel to the lines of force.
The electrical conductivity of crystals also varies with the direction, and bears the same relation to the symmetry as the thermal conductivity. In a rhombohedral crystal of haematite the electrical conductivity along the principal axis is only half as great as in directions perpendicular to this axis; whilst in a crystal of bismuth, which is also rhombohedral, the conductivities along and perpendicular to the axis are as 1.6:1.
Conducting crystals are thermo-electric: when placed against another conducting substance and the contact heated there will be a flow of electricity from one body to the other if the circuit be closed. The thermo-electric force depends not only on the nature of the substance, but also on the direction within the crystal, and may in general be expressed by an ellipsoid. A remarkable case is, however, presented by minerals of the pyrites group: some crystals of pyrites are more strongly thermo-electrically positive than antimony, and others more negative than bismuth, so that the two when placed together give a stronger thermo-electric couple than do antimony and bismuth. In the thermo-electrically positive crystals of pyrites the faces of the pentagonal dodecahedron are striated parallel to the cubic edges, whilst in the rarer negative crystals the faces are striated perpendicular to these edges. Sometimes both sets of striae are present on the same face, and the corresponding areas are then thermo-electrically positive and negative.
The most interesting relation between the symmetry of crystals and their electrical properties is that presented by the pyro-electrical phenomena of certain crystals. This is a phenomenon which may be readily observed, and one which often aids in the determination of the symmetry of crystals. It is exhibited by crystals in which there is no centre of symmetry, and the axes of symmetry are uniterminal or polar in character, being associated with different faces on the crystal at their two ends. When a non-conducting crystal possessing this hemimorphic type of symmetry is subjected to changes of temperature a charge of positive electricity will be developed on the faces in the region of one end of the uniterminal axis, whilst the faces at the opposite end will be negatively charged. With rising temperature the pole which becomes positively charged is called the “analogous pole,” and that negatively charged the “antilogous pole”: with falling temperature the charges are reversed. The phenomenon was first observed in crystals of tourmaline, the principal axis of which is a uniterminal triad axis of symmetry. In crystals of quartz there are three uniterminal dyad axes of symmetry perpendicular to the principal triad axis (which is here similar at its two ends): the dyad axes emerge at the edges of the hexagonal prism, alternate edges of which become positively and negatively charged on change of temperature. In boracite there are four uniterminal triad axes, and the faces of the two tetrahedra perpendicular to them will bear opposite charges. Other examples of pyro-electric crystals are the orthorhombic mineral hemimorphite (called also, for this reason, “electric calamine”) and the monoclinic tartaric acid and cane-sugar, each of which possesses a uniterminal dyad axis of symmetry. In some exceptional cases, e.g. axinite, prehnite, &c., there is no apparent relation between the distribution of the pyro-electric charges and the symmetry of the crystals.
The distribution of the electric charges may be made visible by the following simple method, which may be applied even with minute crystals observed under the microscope. A finely powdered mixture of red-lead and sulphur is dusted through a sieve over the cooling crystal. In passing through the sieve the particles of red-lead and sulphur become electrified by mutual friction, the former positively and the latter negatively. The red-lead is therefore attracted to the negatively charged parts of the crystal and the sulphur to those positively charged, and the distribution of the charges over the whole crystal becomes mapped out in the two colours red and yellow.
Since, when a crystal changes in temperature, it also expands or contracts, a similar distribution of “piezo-electric” (from πιέζειν, to press) charges are developed when a crystal is subjected to changes of pressure in the direction of a uniterminal axis of symmetry. Thus increasing pressure along the principal axis of a tourmaline crystal produces the same electric charges as decreasing temperature.
That the general and physical characters of a chemical substance are profoundly modified by crystalline structure is strikingly illustrated by the two crystalline modifications of the element carbon—namely, diamond and graphite. The former crystallizes in the cubic system, possesses four directions of perfect cleavage, is extremely hard and transparent, is a non-conductor of heat and electricity, and has a specific gravity of 3.5; whilst graphite crystallizes in the hexagonal system, cleaves in a single direction, is very soft and opaque, is a good conductor of heat and electricity, and has a specific gravity of 2.2. Such substances, which are identical in chemical composition, but different in crystalline form and consequently in their physical properties, are said to be “dimorphous.” Numerous examples of dimorphous substances are known; for instance, calcium carbonate occurs in nature either as calcite or as aragonite, the former being rhombohedral and the latter orthorhombic; mercuric iodide crystallizes from solution as red tetragonal crystals, and by sublimation as yellow orthorhombic crystals. Some substances crystallize in three different modifications, and these are said to be “trimorphous”; for example, titanium dioxide is met with as the minerals rutile, anatase and brookite (q.v.). In general, or in cases where more than three crystalline modifications are known (e.g. in sulphur no less than six have been described), the term “polymorphism” is applied.
On the other hand, substances which are chemically quite distinct may exhibit similarity of crystalline form. For example, the minerals iodyrite (AgI), greenockite (CdS), and zincite (ZnO) are practically identical in crystalline form; calcite (CaCO3) and sodium nitrate (NaNO3); celestite (SrSO)4 and marcasite (FeS2); epidote and azurite; and many others, some of which are no doubt only accidental coincidences. Such substances are said to be “homoeomorphous” (Gr. ὅμοιος, like, and μορφή, form).
Similarity of crystalline form in substances which are chemically related is frequently met with and is a relation of much importance: such substances are described as being “isomorphous.” Amongst minerals there are many examples of isomorphous groups, e.g. the rhombohedral carbonates, garnet (q.v.), plagioclase (q.v.); and amongst crystals of artificially prepared salts isomorphism is equally common, e.g. the sulphates and selenates of potassium, rubidium and caesium. The rhombohedral carbonates have the general formula R″CO3, where R″ represents calcium, magnesium, iron, manganese, zinc, cobalt or lead, and the different minerals (calcite, ankerite, magnesite, chalybite, rhodochrosite and calamine (q.v.)) of the group are not only similar in crystalline form, cleavage, optical and other characters, but the angles between corresponding faces do not differ by more than 1° or 2°. Further, equivalent amounts of the different chemical elements represented by R” are mutually replaceable, and two or more of these elements may be present together in the same crystal, which is then spoken of as a “mixed crystal” or isomorphous mixture.
In another isomorphous series of carbonates with the same general formula R″CO3, where R″ represents calcium, strontium, barium, lead or zinc, the crystals are orthorhombic in form, and are thus dimorphous with those of the previous group (e.g. calcite and aragonite, the other members being only represented by isomorphous replacements). Such a relation is known as “isodimorphism.” An even better example of this is presented by the arsenic and antimony trioxides, each of which occurs as two distinct minerals:—
| As2O3, Arsenolite (cubic); Claudetite (monoclinic). Sb2O3, Senarmontite (cubic); Valentinite (orthorhombic). |
Claudetite and valentinite though crystallizing in different systems have the same cleavages and very nearly the same angles, and are strictly isomorphous.
Substances which form isodimorphous groups also frequently crystallize as double salts. For instance, amongst the carbonates quoted above are the minerals dolomite (CaMg(CO3)2) and barytocalcite (CaBa(CO3)2). Crystals of barytocalcite (q.v.) are monoclinic; and those of dolomite (q.v.), though closely related to calcite in angles and cleavage, possess a different degree of symmetry, and the specific gravity is not such as would result by a simple isomorphous mixture of the two carbonates. A similar case is presented by artificial crystals of silver nitrate and potassium nitrate. Somewhat analogous to double salts are the molecular compounds formed by the introduction of “water of crystallization,” “alcohol of crystallization,” &c. Thus sodium sulphate may crystallize alone or with either seven or ten molecules of water, giving rise to three crystallographically distinct substances.
A relation of another kind is the alteration in crystalline form resulting from the replacement in the chemical molecule of one or more atoms by atoms or radicles of a different kind. This is known as a “morphotropic” relation (Gr. μορφή, form, τρόπος, habit). Thus when some of the hydrogen atoms of benzene are replaced by (OH) and (NO2) groups the orthorhombic system of crystallization remains the same as before, and the crystallographic axis a is not much affected, but the axis c varies considerably:—
| a | : b | : c | |
| Benzene, C6H6 | 0·891 | : 1 | : 0·799 |
| Resorcin, C6H4(OH)2 | 0·910 | : 1 | : 0·540 |
| Picric acid, C6H2(OH)(NO2)3 | 0·937 | : 1 | : 0·974 |
A striking example of morphotropy is shown by the humite (q.v.) group of minerals: successive additions of the group Mg2SiO4 to the molecule produce successive increases in the length of the vertical crystallographic axis.
In some instances the replacement of one atom by another produces little or no influence on the crystalline form; this happens in complex molecules of high molecular weight, the “mass effect” of which has a controlling influence on the isomorphism. An example of this is seen in the replacement of sodium or potassium by lead in the alunite (q.v.) group of minerals, or again in such a complex mineral as tourmaline, which, though varying widely in chemical composition, exhibits no variation in crystalline form.
For the purpose of comparing the crystalline forms of isomorphous and morphotropic substances it is usual to quote the angles or the axial ratios of the crystal, as in the table of benzene derivatives quoted above. A more accurate comparison is, however, given by the “topic axes,” which are calculated from the axial ratios and the molecular volume; they express the relative distances apart of the crystal molecules in the axial directions.
The two isomerides of substances, such as tartaric acid, which in solution rotate the plane of polarized light either to the right or to the left, crystallize in related but enantiomorphous forms.
References.—An introduction to crystallography is given in most text-books of mineralogy, e.g. those of H. A. Miers and of E. S. Dana (see Mineralogy). The standard work treating of the subject generally is that of P. Groth, Physikalische Kristallographie (4th ed., Leipzig, 1905). A condensed summary is given by A. J. Moses, The Characters of Crystals (New York, 1899).
For geometrical crystallography, dealing exclusively with the external form of crystals, reference may be made to N. Story-Maskelyne, Crystallography, a Treatise on the Morphology of Crystals (Oxford, 1895) and W. J. Lewis, A Treatise on Crystallography (Cambridge, 1899). Theories of crystal structure are discussed by L. Sohncke, Entwickelung einer Theorie der Krystallstruktur (Leipzig, 1879); A. Schoenflies, Krystallsysteme und Krystallstructur (Leipzig, 1891); and H. Hilton, Mathematical Crystallography and the Theory of Groups of Movements (Oxford, 1903).
The physical properties of crystals are treated by T. Liebisch, Physikalische Krystallographie (Leipzig, 1891), and in a more elementary form in his Grundriss der physikalischen Krystallographie (Leipzig, 1896); E. Mallard, Traité de cristallographie, Cristallographie physique (Paris, 1884); C. Soret, Éléments de cristallographie physique (Geneva and Paris, 1893).
For an account of the relations between crystalline form and chemical composition, see A. Arzruni, Physikalische Chemie der Krystalle (Braunschweig, 1893); A. Fock, An Introduction to Chemical Crystallography, translated by W. J. Pope (Oxford, 1895); P. Groth, An Introduction to Chemical Crystallography, translated by H. Marshall (London, 1906); A. E. H. Tutton, Crystalline Structure and Chemical Constitution, 1910. Descriptive works giving the crystallographic constants of different substances are C. F. Rammelsberg, Handbuch der krystallographisch-physikalischen Chemie (Leipzig, 1881–1882); P. Groth, Chemische Krystallographie (Leipzig, 1906); and of minerals the treatises of J. D. Dana and C. Hintze. (L. J. S.)
- ↑ From the Greek letter δ, Δ; in general, a triangular-shaped object; also an alternative name for a trapezoid.
- ↑ Named after pyrites, which crystallizes in a typical form of this class.
- ↑ πλάγιος, placed sideways, referring to the absence of planes and centre of symmetry.
- ↑ From γῦρος, a ring or spiral, and εἶδος, form.
- ↑ From μόνος, single, and κλίειν, to incline, since one axis is inclined to the plane of the other two axes, which are at right angles.


