ELASTICITY. 1. Elasticity is the property of recovery of an original size or shape. A body of which the size, or shape, or both size and shape, have been altered by the application of forces may, and generally does, tend to return to its previous size and shape when the forces cease to act. Bodies which exhibit this tendency are said to be elastic (from Greek, ἐλαύνειν, to drive). All bodies are more or less elastic as regards size; and all solid bodies are more or less elastic as regards shape. For example: gas contained in a vessel, which is closed by a piston, can be compressed by additional pressure applied to the piston; but, when the additional pressure is removed, the gas expands and drives the piston outwards. For a second example: a steel bar hanging vertically, and loaded with one ton for each square inch of its sectional area, will have its length increased by about seven one-hundred-thousandths of itself, and its sectional area diminished by about half as much; and it will spring back to its original length and sectional area when the load is gradually removed. Such changes of size and shape in bodies subjected to forces, and the recovery of the original size and shape when the forces cease to act, become conspicuous when the bodies have the forms of thin wires or planks; and these properties of bodies in such forms are utilized in the construction of spring balances, carriage springs, buffers and so on.
It is a familiar fact that the hair-spring of a watch can be coiled and uncoiled millions of times a year for several years without losing its elasticity; yet the same spring can have its shape permanently altered by forces which are much greater than those to which it is subjected in the motion of the watch. The incompleteness of the recovery from the effects of great forces is as important a fact as the practical completeness of the recovery from the effects of comparatively small forces. The fact is referred to in the distinction between “perfect” and “imperfect” elasticity; and the limitation which must be imposed upon the forces in order that the elasticity may be perfect leads to the investigation of “limits of elasticity” (see §§ 31, 32 below). Steel pianoforte wire is perfectly elastic within rather wide limits, glass within rather narrow limits; building stone, cement and cast iron appear not to be perfectly elastic within any limits, however narrow. When the limits of elasticity are not exceeded no injury is done to a material or structure by the action of the forces. The strength or weakness of a material, and the safety or insecurity of a structure, are thus closely related to the elasticity of the material and to the change of size or shape of the structure when subjected to forces. The “science of elasticity” is occupied with the more abstract side of this relation, viz. with the effects that are produced in a body of definite size, shape and constitution by definite forces; the “science of the strength of materials” is occupied with the more concrete side, viz. with the application of the results obtained in the science of elasticity to practical questions of strength and safety (see Strength of Materials).
2. Stress.—Every body that we know anything about is always under the action of forces. Every body upon which we can experiment is subject to the force of gravity, and must, for the purpose of experiment, be supported by other forces. Such forces are usually applied by way of pressure upon a portion of the surface of the body; and such pressure is exerted by another body in contact with the first. The supported body exerts an equal and opposite pressure upon the supporting body across the portion of surface which is common to the two. The same thing is true of two portions of the same body. If, for example, we consider the two portions into which a body is divided by a (geometrical) horizontal plane, we conclude that the lower portion supports the upper portion by pressure across the plane, and the upper portion presses downwards upon the lower portion with an equal pressure. The pressure is still exerted when the plane is not horizontal, and its direction may be obliquely inclined to, or tangential to, the plane. A more precise meaning is given to “pressure” below. It is important to distinguish between the two classes of forces: forces such as the force of gravity, which act all through a body, and forces such as pressure applied over a surface. The former are named “body forces” or “volume forces,” and the latter “surface tractions.” The action between two portions of a body separated by a geometrical surface is of the nature of surface traction. Body forces are ultimately, when the volumes upon which they act are small enough, proportional to the volumes; surface tractions, on the other hand, are ultimately, when the surfaces across which they act are small enough, proportional to these surfaces. Surface tractions are always exerted by one body upon another, or by one part of a body upon another part, across a surface of contact; and a surface traction is always to be regarded as one aspect of a “stress,” that is to say of a pair of equal and opposite forces; for an equal traction is always exerted by the second body, or part, upon the first across the surface.
3. The proper method of estimating and specifying stress is a matter of importance, and its character is necessarily mathematical. The magnitudes of the surface tractions which compose a stress are estimated as so much force (in dynes or tons) per unit of area (per sq. cm. or per sq. in.). The traction across an assigned plane at an assigned point is measured by the mathematical limit of the fraction where denotes the numerical measure of the force exerted across a small portion of the plane containing the point, and denotes the numerical measure of the area of this portion, and the limit is taken by diminishing indefinitely. The traction may act as "tension," as it does in the case of a horizontal section of a bar supported at its upper end and hanging vertically, or as "pressure," as it does in the case of a horizontal section of a block resting on a horizontal plane, or again it may act obliquely or even tangentially to the separating plane. Normal tractions are reckoned as positive when they are tensions, negative when they are pressures. Tangential tractions are often called “shears” (see § 7 below). Oblique tractions can always be resolved, by the vector law, into normal and tangential tractions. In a fluid at rest the traction across any plane at any point is normal to the plane, and acts as pressure. For the complete specification of the “state of stress” at any point of a body, we should require to know the normal and tangential components of the traction across every plane drawn through the point. Fortunately this requirement can be very much simplified (see §§ 6, 7 below).
4. In general let denote the direction of the normal drawn in a specified sense to a plane drawn through a point of a body; and let denote the traction exerted across the plane, at the point by the portion of the body towards which is drawn upon the remaining portion. Then is a vector quantity, which has a definite magnitude (estimated as above by the limit of a fraction of the form ) and a definite direction. It can be specified completely by its components referred to fixed rectangular axes of When the direction of is that of the axis of in the positive sense, the components are denoted by and a similar notation is used when the direction of is that of or the suffix being replaced by or
5. Every body about which we know anything is always in a state of stress, that is to say there are always internal forces acting between the parts of the body, and these forces are exerted as surface tractions across geometrical surfaces drawn in the body. The body, and each part of the body, moves under the action of all the forces (body forces and surface tractions) which are exerted upon it; or remains at rest if these forces are in equilibrium. This result is expressed analytically by means of certain equations—the “equations of motion” or “equations of equilibrium” of the body.
Let denote the density of the body at any point, the components parallel to the axes of of the body forces, estimated as so much force per unit of mass; further let denote the components, parallel to the same axes, of the acceleration of the particle which is momentarily at the point (). The equations of motion express the result that the rates of change of the momentum, and of the moment of momentum, of any portion of the body are those due to the action of all the forces exerted upon the portion by other bodies, or by other portions of the same body. For the changes of momentum, we have three equations of the type
| (1) |
in which the volume integrations are taken through the volume of the portion of the body, the surface integration is taken over its surface, and the notation is that of § 4, the direction of being that of the normal to this surface drawn outwards. For the changes of moment of momentum, we have three equations of the type
| (2) |
The equations (1) and (2) are the equations of motion of any kind of body. The equations of equilibrium are obtained by replacing the right-hand members of these equations by zero.
6. These equations can be used to obtain relations between the values of for different directions When the equations are applied to a very small volume, it appears that the terms expressed by surface integrals would, unless they tend to zero limits in a higher order than the areas of the surfaces, be very great compared with the terms expressed by volume integrals. We conclude that the surface tractions on the portion of the body which is bounded by any very small closed surface, are ultimately in equilibrium. When this result is interpreted for a small portion in the shape of a tetrahedron, having three of its faces at right angles to the co-ordinate axes, it leads to three equations of the type
| (1) |
where is the direction of the normal (drawn outwards) to the remaining face of the tetrahedron, and denote the angles which this normal makes with the axes. Hence for any direction are expressed in terms of When the above result is interpreted for a very small portion in the shape of a cube, having its edges parallel to the co-ordinate axes, it leads to the equations
| (2) |
When we substitute in the general equations the particular results which are thus obtained, we find that the equations of motion take such forms as
| (3) |
and the equations of moments are satisfied identically. The equations of equilibrium are obtained by replacing the right-hand members by zero.

Fig. 17. A state of stress in which the traction across any plane of a set of parallel planes is normal to the plane, and that across any perpendicular plane vanishes, is described as a state of “simple tension” (“simple pressure” if the traction is negative). A state of stress in which the traction across any plane is normal to the plane, and the traction is the same for all planes passing through any point, is described as a state of “uniform tension” (“uniform pressure” if the traction is negative). Sometimes the phrases “isotropic tension” and “hydrostatic pressure” are used instead of “uniform” tension or pressure. The distinction between the two states, simple tension and uniform tension, is illustrated in fig. 1.
A state of stress in which there is purely tangential traction on a plane, and no normal traction on any perpendicular plane, is described as a state of “shearing stress.” The result (2) of § 6 shows that tangential tractions occur in pairs. If, at any point, there is tangential traction, in any direction, on a plane parallel to this direction, and if we draw through the point a plane at right angles to the direction of this traction, and therefore containing the normal to the first plane, then there is equal tangential traction on this second plane in the direction of the normal to the first plane. The result is illustrated in fig. 2, where a rectangular block is subjected on two opposite faces to opposing tangential tractions, and is held in equilibrium by equal tangential tractions applied to two other faces. 
Fig. 2
Through any point there always pass three planes, at right angles to each other, across which there is no tangential traction. These planes are called the “principal planes of stress,” and the (normal) tractions across them the “principal stresses.” Lines, usually curved, which have at every point the direction of a principal stress at the point, are called “lines of stress.”
8. It appears that the stress at any point of a body is completely specified by six quantities, which can be taken to be the and of § 6. The first three are tensions (pressures if they are negative) across three planes parallel to fixed rectangular directions, and the remaining three are tangential tractions across the same three planes. These six quantities are called the “components of stress.” It appears also that the components of stress are connected with each other, and with the body forces and accelerations, by the three partial differential equations of the type (3) of § 6. These equations are available for the purpose of determining the state of stress which exists in a body of definite form subjected to definite forces, but they are not sufficient for the purpose (see § 38 below). In order to effect the determination it is necessary to have information concerning the constitution of the body, and to introduce subsidiary relations founded upon this information.
9. The definite mathematical relations which have been found to connect the components of stress with each other, and with other quantities, result necessarily from the formation of a clear conception of the nature of stress. They do not admit of experimental verification, because the stress within a body does not admit of direct measurement. Results which are deduced by the aid of these relations can be compared with experimental results. If any discrepancy were observed it would not be interpreted as requiring a modification of the concept of stress, but as affecting some one or other of the subsidiary relations which must be introduced for the purpose of obtaining the theoretical result.
10. Strain.—For the specification of the changes of size and shape which are produced in a body by any forces, we begin by defining the “average extension” of any linear element or “filament” of the body. Let be the length of the filament before the forces are applied, its length when the body is subjected to the forces. The average extension of the filament is measured by the fraction If this fraction is negative there is “contraction.” The “extension at a point” of a body in any assigned direction is the mathematical limit of this fraction when one end of the filament is at the point, the filament has the assigned direction, and its length is diminished indefinitely. It is clear that all the changes of size and shape of the body are known when the extension at every point in every direction is known.
The relations between the extensions in different directions around the same point are most simply expressed by introducing the extensions in the directions of the co-ordinate axes and the angles between filaments of the body which are initially parallel to these axes. Let denote the extensions parallel to the axes of and let denote the cosines of the angles between the pairs of filaments which are initially parallel to the axes of and and and Also let denote the extension in the direction of a line the direction cosines of which are Then, if the changes of size and shape are slight, we have the relation
The body which undergoes the change of size or shape is said to be “strained,” and the “strain” is determined when the quantities and defined above are known at every point of it. These quantities are called “components of strain.” The three of the type are extensions, and the three of the type are called “shearing strains” (see § 12 below).
11. All the changes of relative position of particles of the body are known when the strain is known, and conversely the strain can be determined when the changes of relative position are given. These changes can be expressed most simply by the introduction of a vector quantity to represent the displacement of any particle.
When the body is deformed by the action of any forces its particles pass from the positions which they occupied before the action of the forces into new positions. If are the co-ordinates of the position of a particle in the first state, its co-ordinates in the second state may be denoted by The quantities, are the “components of displacement.” When these quantities are small, the strain is connected with them by the equations
| . (1) | |||
13. Besides enabling us to express the extension in aniy direction and the changes of relative direction of any filaments of the body, the components of strain also express the changes of size of volumes and areas. In particular, the “cubical dilatation,” that is to say, the increase of volume per unit of volume, is expressed by the quantity or When this quantity is negative there is “compression.”
14. It is important to distinguish between two types of strain: the “rotational” type and the “irrotational” type. The distinction is illustrated in fig. 3, where the figure is obtained from the figure by contraction parallel to and extension parallel to and the figure can be obtained from by the same contraction and extension followed by a rotation through the angle In strains of the irrotational type there are at any point three filaments at right angles to each other, which are such that the particles which lie in them before strain continue to lie in them after strain. A small spherical element of the body with its centre at the point becomes a small ellipsoid with its axes in the directions of these three filaments. In the case illustrated in the figure, the lines of the filaments in question, when the figure is strained into the figure are and a line through at right angles to their plane. In strains of the rotational type, on the other hand, the single existing set of three filaments (issuing from a point) which cut each other at right angles both before and after strain do not retain their directions after strain, though one of them may do so in certain cases. In the figure, the lines of the filaments in question, when the figure is strained into are and a line at right angles to their plane before strain, and after strain they are and the same third line. A rotational strain can always be analysed into an irrotational strain (or “pure” strain) followed by a rotation.
Analytically, a strain is irrotational if the three quantities
15. Whether the strain is rotational or not, there is always one set of three linear elements issuing from any point which cut each other at right angles both before and after strain, If these directions are chosen as axes of the shearing strains vanish at this point. These directions are called the “principal axes of strain,” and the extensions in the directions of these axes the “principal extensions.”
16. It is very important to observe that the relations between components of strain and components of displacement imply relations between the components of strain themselves. If by any process of reasoning we arrive at the conclusion that the state of strain in a body is such and such a state, we have a test of the possibility or impossibility of our conclusion. The test is that, if the state of strain is a possible one, then there must be a displacement which can be associated with it in accordance with the equations (1) of § 11.
We may eliminate from these equations. When this is done we find that the quantities are connected by the two sets of equations
| . . . (1) | |
and
| . . (2) | |
These equations are known as the conditions of compatibility of strain-components. The components of strain which specify any possible strain satisfy them. Quantities arrived at in any way, and intended to be components of strain, if they fail to satisfy these equations, are not the components of any possible strain; and the theory or speculation by which they are reached must be modified or abandoned.
When the components of strain have been found in accordance with these and other necessary equations, the displacement is to be found by solving the equations (1) of § 11, considered as differential equations to determine The most general possible solution will differ from any other solution by terms which contain arbitrary constants, and these terms represent a possible displacement. This “complementary displacement” involves no strain, and would be a possible displacement of an ideal perfectly rigid body.
17. The relations which connect the strains with each other and with the displacement are geometrical relations resulting from the definitions of the quantities and not requiring any experimental verification. They do not admit of such verification, because the strain within a body cannot be measured. The quantities (belonging to the same category) which can be measured are displacements of points on the surface of a body. For example, on the surface of a bar subjected to tension we may make two fine transverse scratches, and measure the distance between them before and after the bar is stretched. For such measurements very refined instruments are required. Instruments for this purpose are called barbarously “extensometers,” and many different kinds have been devised. From measurements of displacement by an extensometer we may deduce the average extension of a filament of the bar terminated by the two scratches. In general, when we attempt to measure a strain, We really measure some displacements, and deduce the values, not of the strain at a point, but of the average extensions of some particular linear filaments of a body containing the point; and these filaments are, from the nature of the case, nearly always superficial filaments.
18. In the case of transparent materials such as glass there is available a method of studying experimentally the state of strain within a body. This method is founded upon the result that a piece of glass when strained becomes doubly refracting, with its optical principal axes at any point in the directions of the principal axes of strain (§ 15) at the point. When the piece has two parallel plane faces, and two of the principal axes of strain at any point are parallel to these faces, polarized light transmitted through the piece in a direction normal to the faces can be used to determine the directions of the principal axes of the strain at any point. If the directions of these axes are known theoretically the comparison of the experimental and theoretical results yields a test of the theory.
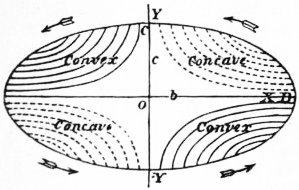
19. Relations between Stresses and Strains.—The problem of the extension of a bar subjected to tension is the one which has been most studied experimentally, and as a result of this study it is found that for most materials, including all metals except cast metals, the measurable extension is proportional to the applied tension, provided that this tension is not too great. In interpreting this result it is assumed that the tension is uniform over the cross-section of the bar, and that the extension of longitudinal filaments is uniform throughout the bar; and then the result takes the form of a law of proportionality connecting stress and strain: The tension is proportional to the extension. Similar results are found for the same materials when other methods of experimenting are adopted, for example, when a bar is supported at the ends and bent by an attached load and the deflexion is measured, or when a bar is twisted by an axial couple and the relative angular displacement of two sections is measured. We have thus very numerous experimental verifications of the famous law first enunciated by Robert Hooke in 1678 in the words “Ut Tensio sic vis”; that is, “the Power of any spring is in the same proportion as the Tension (—stretching) thereof.” The most general statement of Hooke’s Law in modern language would be:—Each of the six components of stress at any point of a body is a linear function of the six components of strain at the point. It is evident from what has been said above as to the nature of the measurement of stresses and strains that this law in all its generality does not admit of complete experimental verification, and that the evidence for it consists largely in the agreement of the results which are deduced from it in a theoretical fashion with the results of experiments. Of such results one of a general character may be noted here. If the law is assumed to be true, and the equations of motion of the body (§ 5) are transformed by means of it into differential equations for determining the components of displacement, these differential equations admit of solutions which represent periodic vibratory displacements (see § 85 below). The fact that solid bodies can be thrown into states of isochronous vibration has been emphasized by G. G. Stokes as a peremptory proof of the truth of Hooke’s Law.
20. According to the statement of the generalized Hooke’s Law the stress-components vanish when the strain-components vanish. The strain-components contemplated in experiments upon which the law is founded are measured from a zero of reckoning which corresponds to the state of the body subjected to experiment before the experiment is made, and the stress-components referred to in the statement of the law are those which are called into action by the forces applied to the body in the course of the experiment. No account is taken of the stress which must already exist in the body owing to the force of gravity and the forces by which the body is supported. When it is desired to take account of this stress it is usual to suppose that the strains which would be produced in the body if it could be freed from the action of gravity and from the pressures of supports are so small that the strains produced by the forces which are applied in the course of the experiment can be compounded with them by simple superposition. This supposition comes to the same thing as measuring the strain in the body, not from the state in which it was before the experiment, but from an ideal state (the “unstressed” state) in which it would be entirely free from internal stress, and allowing for the strain which would be produced by gravity and the supporting forces if these forces were applied to the body when free from stress. In most practical cases the initial strain to be allowed for is unimportant (see §§ 91-93 below).
21. Hooke’s law of proportionality of stress and strain leads to the introduction of important physical constants: the moduluses of elasticity of a body. Let a bar of uniform section (of area ) be stretched with tension which is distributed uniformly over the section, so that the stretching force is and let the bar be unsupported at the sides. The bar will undergo a longitudinal extension of magnitude where is a constant quantity depending upon the material. This constant is called Young's modulus after Thomas Young, who introduced it into the science in 1807. The quantity is of the same nature as a traction, that is to say, it is measured as a force estimated per unit of area. For steel it is about 2.04 × 1012 dynes per square centimetre, or about 13,000 tons per sq. in.
22. The longitudinal extension of the bar under tension is not the only strain in the bar. It is accompanied by a lateral contraction by which all the transverse filaments of the bar are shortened. The amount of this contraction is where is a certain number called Poisson’s ratio, because its importance was at first noted by S. D. Poisson in 1828. Poisson arrived at the existence of this contraction, and the corresponding number from theoretical considerations, and his theory led him to assign to the value Many experiments have been made with the view of determining with the result that it has been found to be different for different materials, although for very many it does not differ much from For steel the best value (Amagat’s) is 0.268. Poisson’s theory admits of being modified so as to agree with the results of experiment.
23. The behaviour of an elastic solid body, strained within the limits of its elasticity, is entirely determined by the constants and if the body is isotropic, that is to say, if it has the same quality in all directions around any point. Nevertheless it is convenient to introduce other constants which are related to the action of particular sorts of forces. The most important of these are the “modulus of compression” (or “bulk modulus”) and the “rigidity” (or “modulus of shear”). To define the modulus of compression, we suppose that a solid body of any form is subjected to uniform hydrostatic pressure of amount p. The state of stress within it will be one of uniform pressure, the same at all points, and the same in all directions round any point. There will be compression, the same at all points, and proportional to the pressure; and the amount of the compression can be expressed as The quantity is the modulus of compression. In this case the linear contraction in any direction is ; but in general the linear extension (or contraction) is not one-third of the cubical dilatation (or compression).
24. To define the rigidity, we suppose that a solid body is subjected to forces in such a way that there is shearing stress within it. For example, a cubical block may be subjected to opposing tractions on opposite faces acting in directions which are parallel to an edge of the cube and to both the faces. Let be the amount of the traction, and let it be uniformly distributed over the faces. As we have seen (§ 7), equal tractions must act upon two other faces in suitable directions in order to maintain equilibrium (see fig. 2 of § 7). The two directions involved may be chosen as axes of as in that figure. Then the state of stress will be one in which the stress-component denoted by is equal to and the remaining stress-components vanish; and the strain produced in the body is shearing strain of the type denoted by The amount of the shearing strain is and the quantity is the “rigidity.”
25. The modulus of compression and the rigidity are quantities of the same kind as Young’s modulus. The modulus of compression of steel is about 1.43 × 1012 dynes per square centimetre, the rigidity is about 8.19 × 1011 dynes per square centimetre. It must be understood that the values for different specimens of nominally the same material may differ considerably.
The modulus of compression and the rigidity of an isotropic material are connected with the Young’s modulus and Poisson’s ratio of the material by the equations
26. Whatever the forces acting upon an isotropic solid body may be, provided that the body is strained within its limits of elasticity, the strain-components are expressed in terms of the stress-components by the equations
| . . (1) | ||
If we introduce a quantity of the same nature as or by the equation}}
| (2) |
| . (3) | ||
and then the behaviour of the body under the action of any forces depends upon the two constants and These two constants were introduced by G. Lamé in his treatise of 1852. The importance of the quantity had been previously emphasized by L. J. Vicat and G. G. Stokes.
27. The potential energy per unit of volume (often called the “resilience”) stored up in the body by the strain is equal to
or the equivalent expression
The former of these expressions is called the “strain-energy-function.”
28. The Young’s modulus of a material is often determined experimentally by the direct method of the extensometer (§ 17), but more frequently it is determined indirectly by means of a result obtained in the theory of the flexure of a bar (see §§ 47, 53 below). The rigidity is usually determined indirectly by means of results obtained in the theory of the torsion of a bar (see §§ 41, 42 below). The modulus of compression may be determined directly by means of the piezometer, as was done by E. H. Amagat, or it may be determined indirectly by means of a result obtained in the theory of a tube under pressure, as was done by A. Mallock (see § 78 below). The value of Poisson’s ratio is generally inferred from the relation connecting it with and or with and but it may also be determined indirectly by means of a result obtained in the theory of the flexure of a bar (§ 47 below), as was done by M. A. Cornu and A. Mallock, or directly by a modification of the extensometer method, as has been done recently by J. Morrow.
29. The elasticity of a fluid is always expressed by means of a single quantity of the same kind as the modulus of compression of a solid body. To any increment of pressure, which is not too great, there corresponds a proportional cubical compression, and the amount of this compression for an increment of pressure can be expressed as The quantity that is usually tabulated is the reciprocal of and it is called the coefficient of compressibility. It is the amount of compression per unit increase of pressure. As a physical quantity it is of the same dimensions as the reciprocal of a pressure (or of a force per unit of area). The pressures concerned are usually measured in atmospheres (1 atmosphere = 1.014 × 106 dynes per sq. cm.). For water the coefficient of compressibility, or the compression per atmosphere, is about 4.5 × 10–5. This gives for the value 2.22 × 1010 dynes per sq. cm. The Young’s modulus and the rigidity of a fluid are always zero.
30. The relations between stress and strain in a material which is not isotropic are much more complicated. In such a material the Young’s modulus depends upon the direction of the tension, and its variations about a point are expressed by means of a surface of the fourth degree. The Poisson’s ratio depends upon the direction of the contracted lateral filaments as well as upon that of the longitudinal extended ones. The rigidity depends upon both the directions involved in the specification of the shearing stress. In general there is no simple relation between the Young’s moduluses and Poisson’s ratios and rigidities for assigned directions and the modulus of compression. Many materials in common use, all fibrous woods for example, are actually aeolotropic (that is to say, are not isotropic), but the materials which are aeolotropic in the most regular fashion are natural crystals. The elastic behaviour of crystals has been studied exhaustively by many physicists, and in particular by W. Voigt. The strain-energy-function is a homogeneous quadratic function of the six strain-components, and this function may have as many as 21 independent coefficients, taking the place in the general case of the 2 coefficients which occur when the material is isotropic—a result first obtained by George Green in 1837. The best experimental determinations of the coefficients have been made indirectly by Voigt by means of results obtained in the theories of the torsion and flexure of aeolotropic bars.
31. Limits of Elasticity.—A solid body which has been strained by considerable forces does not in general recover its original size and shape completely after the forces cease to act. The strain that is left is called set. If set occurs the elasticity is said to be “imperfect,” and the greatest strain (or the greatest load) of any specified type, for which no set occurs, defines the “limit of perfect elasticity” corresponding to the specified type of strain, or of stress. All fluids and many solid bodies, such as glasses and crystals, as well as some metals (copper, lead, silver) appear to be perfectly elastic as regards change of volume within wide limits; but malleable metals and alloys can have their densities permanently increased by considerable pressures. The limits of perfect elasticity as regards change of shape, on the other hand, are very low, if they exist at all, for glasses and other hard, brittle solids; but a class of metals including copper, brass, steel, platinum are very perfectly elastic as regards distortion, provided that the distortion is not too great. The question can be tested by observation of the torsional elasticity of thin fibres or wires. The limits of perfect elasticity are somewhat ill-defined, because an experiment cannot warrant us in asserting that there is no set, but only that, if there is any set, it is too small to be observed.
32. A different meaning may be, and often is, attached to the phrase “limits of elasticity” in consequence of the following experimental result:—Let a bar be held stretched under a moderate tension, and let the extension be measured; let the tension be slightly increased and the extension again measured; let this process be continued, the tension being increased by equal increments. It is found that when the tension is not too great the extension increases by equal increments (as nearly as experiment can decide), but that, as the tension increases, a stage is reached in which the extension increases faster than it would do if it continued to be proportional to the tension. The beginning of this stage is tolerably well marked. Some time before this stage is reached the limit of perfect elasticity is passed; that is to say, if the load is removed it is found that there is some permanent set. The limiting tension beyond which the above law of proportionality fails is often called the “limit of linear elasticity.” It is higher than the limit of perfect elasticity. For steel bars of various qualities J. Bauschinger found for this limit values varying from 10 to 17 tons per square inch. The result indicates that, when forces which produce any kind of strain are applied to a solid body and are gradually increased, the strain at any instant increases proportionally to the forces up to a stage beyond that at which, if the forces were removed, the body would completely recover its original size and shape, but that the increase of strain ceases to be proportional to the increase of load when the load surpasses a certain limit. There would thus be, for any type of strain, a limit of linear elasticity, which exceeds the limit of perfect elasticity.
33. A body which has been strained beyond the limit of linear elasticity is often said to have suffered an “over-strain.” When the load is removed, the set which can be observed is not entirely permanent; but it gradually diminishes with lapse of time. This phenomenon is named “elastic after-working.” If, on the other hand, the load is maintained constant, the strain is gradually increased. This effect indicates a gradual flowing of solid bodies under great stress; and a similar effect was observed in the experiments of H. Tresca on the punching and crushing of metals. It appears that all solid bodies under sufficiently great loads become “plastic,” that is to say, they take a set which gradually increases with the lapse of time. No plasticity is observed when the limit of linear elasticity is not exceeded.
34. The values of the elastic limits are affected by overstrain. If the load is maintained for some time, and then removed, the limit of linear elasticity is found to be higher than before. If the load is not maintained, but is removed and then reapplied, the limit is found to be lower than before. During a period of rest a test piece recovers its elasticity after overstrain.
35. The effects of repeated loading have been studied by A. Wöhler, J. Bauschinger, O. Reynolds and others. It has been found that, after many repetitions of rather rapidly alternating stress, pieces are fractured by loads which they have many times withstood. It is not certain whether the fracture is in every case caused by the gradual growth of minute flaws from the beginning of the series of tests, or whether the elastic quality of the material suffers deterioration apart from such flaws. It appears, however, to be an ascertained result that, so long as the limit of linear elasticity is not exceeded, repeated loads and rapidly alternating loads do not produce failure of the material.
36. The question of the conditions of safety, or of the conditions in which rupture is produced, is one upon which there has been much speculation, but no completely satisfactory result has been obtained. It has been variously held that rupture occurs when the numerically greatest principal stress exceeds a certain limit, or when this stress is tension and exceeds a certain limit, or when the greatest difference of two principal stresses (called the “stress-difference”) exceeds a certain limit, or when the greatest extension or the greatest shearing strain or the greatest strain of any type exceeds a certain limit. Some of these hypotheses appear to have been disproved. It was held by G. F. Fitzgerald (Nature, Nov. 5, 1896) that rupture is not produced by pressure symmetrically applied all round a body, and this opinion has been confirmed by the recent experiments of A. Föppl. This result disposes of the greatest stress hypothesis and also of the greatest strain hypothesis. The fact that short pillars can be crushed by longitudinal pressure disposes of the greatest tension hypothesis, for there is no tension in the pillar. The greatest extension hypothesis failed to satisfy some tests imposed by H. Wehage, who experimented with blocks of wrought iron subjected to equal pressures in two directions at right angles to each other. The greatest stress difference hypothesis and the greatest shearing strain hypothesis would lead to practically identical results, and these results have been held by J. J. Guest to accord well with his experiments on metal tubes subjected to various systems of combined stress; but these experiments and Guest’s conclusion have been criticized adversely by O. Mohr, and the question cannot be regarded as settled. The fact seems to be that the conditions of rupture depend largely upon the nature of the test (tensional, torsional, flexural, or whatever it may be) that is applied to a specimen, and that no general formula holds for all kinds of tests. The best modern technical writings emphasize the importance of the limits of linear elasticity and of tests of dynamical resistance (§ 87 below) as well as of statical resistance.
37. The question of the conditions of rupture belongs rather to the science of the strength of materials than to the science of elasticity (§ 1); but it has been necessary to refer to it briefly here, because there is no method except the methods of the theory of elasticity for determining the state of stress or strain in a body subjected to forces. Whatever view may ultimately be adopted as to the relation between the conditions of safety of a structure and the state of stress or strain in it, the calculation of this state by means of the theory or by experimental means (as in § 18) cannot be dispensed with.
38. Methods of determining the Stress in a Body subjected to given Forces.—To determine the state of stress, or the state of strain, in an isotropic solid body strained within its limits of elasticity by given forces, we have to use (i.) the equations of equilibrium, (ii.) the conditions which hold at the bounding surface, (iii.) the relations between stress-components and strain-components, (iv.) the relations between strain-components and displacement. The equations of equilibrium are (with notation already used) three partial differential equations of the type
| (1) |
The conditions which hold at the bounding surface are three equations of the type
| (2) |
where denotes the direction of the outward-drawn normal to the bounding surface, and denotes the -component of the applied surface traction. The relations between stress-components and strain-components are expressed by either of the sets of equations (1) or (3) of § 26. The relations between, strain-components and displacement are the equations (1) of § 11, or the equivalent conditions of compatibility expressed in equations (1) and (2) of § 16.
39. We may proceed by either of two methods. In one method we eliminate the stress-components and the strain-components and retain only the components of displacement. This method leads (with notation already used) to three partial differential equations of the type
| (3) |
and three boundary conditions of the type
| (4) |
In the alternative method we eliminate the strain-components and the displacements. This method leads to a system of partial differential equations to be satisfied by the stress-components. In this system there are three equations of the type
| (1 bis) |
three of the type
| (5) |
and three of the type
| (6) |
the equations of the two latter types being necessitated by the conditions of compatibility of strain-components. The solutions of these equations have to be adjusted so that the boundary conditions of the type (2) may be satisfied.
40. It is evident that whichever method is adopted the mathematical problem is in general very complicated. It is also evident that, if we attempt to proceed by help of some intuition as to the nature of the stress or strain, our intuition ought to satisfy the tests provided by the above systems of equations. Neglect of this precaution has led to many errors. Another source of frequent error lies in the neglect of the conditions in which the above systems of equations are correct. They are obtained by help of the supposition that the relative displacements of the parts of the strained body are small. The solutions of them must therefore satisfy the test of smallness of the relative displacements.
41. Torsion.—As a first example of the application of the theory we take the problem of the torsion of prisms. This problem, considered first by C. A. Coulomb in 1784, was finally solved by B. de Saint-Venant in 1855. The problem is this:—A cylindrical or prismatic bar is held twisted by terminal couples; it is required to determine the state of stress and strain in the interior. When the bar is a circular cylinder the problem is easy. Any section is displaced by rotation about the central-line through a small angle, which is proportional to the distance of the section from a fixed plane at right angles to this line. This plane is a terminal section if one of the two terminal sections is not displaced. The angle through which the section rotates is where is a constant, called the amount of the twist; and this constant is equal to where is the twisting couple, and is the moment of inertia of the cross-section about the central-line. This result is often called “Coulomb’s law.” The stress within the bar is shearing stress, consisting, as it must, of two sets of equal tangential tractions on two sets of planes which are at right angles to each other. These planes are the cross-sections and the axial planes of the bar. The tangential traction at any point of the cross-section is directed at right angles to the axial plane through the point, and the tangential traction on the axial plane is directed parallel to the length of the bar. The amount of either at a distance r from the axis is or The result that can be used to determine experimentally, for may be measured and and are known.
42. When the cross-section of the bar is not circular it is clear that this solution fails; for the existence of tangential traction, near the prismatic bounding surface, on any plane which does not cut this surface at right angles, implies the existence of traction applied to this surface. We may attempt to modify the theory by retaining the supposition that the stress consists of shearing stress, involving tangential traction distributed in some way over the cross-sections. Such traction is obviously a necessary constituent of any stress-system which could be produced by terminal couples around the axis. We should then know that there must be equal tangential traction directed along the length of the bar, and exerted across some planes or other which are parallel to this direction. We should also know that, at the bounding surface, these planes must cut this surface at right angles. The corresponding strain would be shearing strain which could involve (i.) a sliding of elements of one cross-section relative to another, (ii.) a relative sliding of elements of the above mentioned planes in the direction of the length of the bar. We could conclude that there may be a longitudinal displacement of the elements of the cross-sections. We should then attempt to satisfy the conditions of the problem by supposing that this is the character of the strain, and that the corresponding displacement consists of (i.) a rotation of the cross-sections in their planes such as we found in the case of the circle, (ii.) a distortion of the cross-sections into curved surfaces by a displacement (w) which is directed normally to their planes and varies in some manner from point to point of these planes. We could show that all the conditions of the problem are satisfied by this assumption, provided that the longitudinal displacement (w), considered as a function of the position of a point (x, y) in the cross-section, satisfies the equation
| ∂2w | + | ∂2w | = 0, |
| ∂x2 | ∂y2 |
and the boundary condition
| ( | ∂w | − τy) cos(x,ν) + ( | ∂w | + τx) cos(y,ν) = 0, |
| ∂x | ∂y |
where τ denotes the amount of the twist, and ν the direction
of the normal to the boundary. The solution is known for a
great many forms of section. (In the particular case of a circular
section w vanishes.) The tangential traction at any point of
the cross-section is directed along the tangent to that curve
of the family ψ = const. which passes through the point, ψ being
the function determined by the equations
| ∂w | = τ ( | ∂ψ | + y ), | ∂w | = − τ ( | ∂ψ | + x ). |
| ∂x | ∂y | ∂y | ∂x |
The amount of the twist τ produced by terminal couples of magnitude G is G/C, where C is a constant, called the “torsional rigidity” of the prism, and expressed by the formula
| C = μ ( | ∂ψ | ) | 2 | + ( | ∂ψ | ) | 2 | dxdy, |
| ∂x | ∂y |
the integration being taken over the cross-section. When the coefficient of μ in the expression for C is known for any section, μ can be determined by experiment with a bar of that form of section.
 |  |
| Fig. 4. | Fig. 5. |
43. The distortion of the cross-sections into curved surfaces is shown graphically by drawing the contour lines (w = const.). In general the section is divided into a number of compartments, and the portions that lie within two adjacent compartments are respectively concave and convex. This result is illustrated in the accompanying figures (fig. 4 for the ellipse, given by x2/b2 + y2/c2 = 1; fig. 5 for the equilateral triangle, given by (x + 13a) (x2 − 3y2 − 43ax + 49a2) = 0; fig. 6 for the square).
44. The distribution of the shearing stress over the cross-section is determined by the function ψ, already introduced. If we draw the curves ψ = const., corresponding to any form of section, for equidifferent values of the constant, the tangential traction at any point on the cross-section is directed along the tangent to that curve of the family which passes through the point, and the magnitude of it is inversely proportional to the distance between consecutive curves of the family. Fig. 7 illustrates the result in the case of the equilateral triangle. The boundary is, of course, one of the lines. The “lines of shearing stress” which can thus be drawn are in every case identical with the lines of flow of frictionless liquid filling a cylindrical vessel of the same cross-section as the bar, when the liquid circulates in the plane of the section with uniform spin. They are also the same as the contour lines of a flexible and slightly extensible membrane, of which the edge has the same form as the bounding curve of the cross-section of the bar, when the membrane is fixed at the edge and slightly deformed by uniform pressure.
 |
| Fig. 6. |
 |
| Fig. 7. |
45. Saint-Venant’s theory shows that the true torsional rigidity is in general less than that which would be obtained by extending Coulomb’s law (G = μτI) to sections which are not circular. For an elliptic cylinder of sectional area ω and moment of inertia I about its central-line the torsional rigidity is μω4 / 4π2I, and this formula is not far from being correct for a very large number of sections. For a bar of square section of side a centimetres, the torsional rigidity in C.G.S. units is (0.1406) μa4 approximately, μ being expressed in dynes per square centimetre. How great the defect of the true value from that given by extending Coulomb’s law may be in the case of sections with projecting corners is shown by the diagrams (fig. 8 especially no. 4). In these diagrams the upper of the two numbers under each figure indicates the fraction which the true torsional rigidity corresponding to the section is of that value which would be obtained by extending Coulomb’s law; and the lower of the two numbers indicates the ratio which the torsional rigidity for a bar of the corresponding section bears to that of a bar of circular section of the same material and of equal sectional area. These results have an important practical application, inasmuch as they show that strengthening ribs and projections, such as are introduced in engineering to give stiffness to beams, have the reverse of a good effect when torsional stiffness is an object, although they are of great value in increasing the resistance to bending. The theory shows further that the resistance to torsion is very seriously diminished when there is in the surface any dent approaching to a re-entrant angle. At such a place the shearing strain tends to become infinite, and some permanent set is produced by torsion. In the case of a section of any form, the strain and stress are greatest at points on the contour, and these points are in many cases the points of the contour which are nearest to the centroid of the section. The theory has also been applied to show that a longitudinal flaw near the axis of a shaft transmitting a torsional couple has little influence on the strength of the shaft, but that in the neighbourhood of a similar flaw which is much nearer to the surface than to the axis the shearing strain may be nearly doubled, and thus the possibility of such flaws is a source of weakness against which special provision ought to be made.
 |
| Fig. 8.—Diagrams showing Torsional Rigidities. |
 |
| Fig. 9. |
46. Bending of Beams.—As a second example of the application of the general theory we take the problem of the flexure of a beam. In this case also we begin by forming a simple intuition as to the nature of the strain and the stress. On the side of the beam towards the centre of curvature the longitudinal filaments must be contracted, and on the other side they must be extended. If we assume that the cross-sections remain plane, and that the central-line is unaltered in length, we see (at once from fig. 9) that the extensions (or contractions) are given by the formula y/R, where y denotes the distance of a longitudinal filament from the plane drawn through the unstrained central-line at right-angles to the plane of bending, and R is the radius of curvature of the curve into which this line is bent (shown by the dotted line in the figure). Corresponding to this strain there must be traction acting across the cross-sections. If we assume that there is no other stress, then the magnitude of the traction in question is Ey/R, where E is Young’s modulus, and it is tension on the side where the filaments are extended and pressure on the side where they are contracted. If the plane of bending contains a set of principal axes of the cross-sections at their centroids, these tractions for the whole cross-section are equivalent to a couple of moment EI/R, where I now denotes the moment of inertia of the cross-section about an axis through its centroid at right angles to the plane of bending, and the plane of the couple is the plane of bending. Thus a beam of any form of section can be held bent in a “principal plane” by terminal couples of moment M, that is to say by a “bending moment” M; the central-line will take a curvature M/EI, so that it becomes an arc of a circle of radius EI/M; and the stress at any point will be tension of amount My/I, where y denotes distance (reckoned positive towards the side remote from the centre of curvature) from that plane which initially contains the central-line and is at right angles to the plane of the couple. This plane is called the “neutral plane.” The restriction that the beam is bent in a principal plane means that the plane of bending contains one set of principal axes of the cross-sections at their centroids; in the case of a beam of rectangular section the plane would bisect two opposite edges at right angles. In order that the theory may hold good the radius of curvature must be very large.
 |
| Fig. 10. |
 |
| Fig. 11. |
47. In this problem of the bending of a beam by terminal couples the stress is tension, determined as above, and the corresponding strain consists therefore of longitudinal extension of amount My/EI or y/R (contraction if y is negative), accompanied by lateral contraction of amount σMy/EI or σy/R (extension if y is negative), σ being Poisson’s ratio for the material. Our intuition of the nature of the strain was imperfect, inasmuch as it took no account of these lateral strains. The necessity for introducing them was pointed out by Saint-Venant. The effect of them is a change of shape of the cross-sections in their own planes. This is shown in an exaggerated way in fig. 10, where the rectangle ABCD represents the cross-section of the unstrained beam, or a rectangular portion of this cross-section, and the curvilinear figure A′B′C′D′ represents in an exaggerated fashion the cross-section (or the corresponding portion of the cross-section) of the same beam, when bent so that the centre of curvature of the central-line (which is at right angles to the plane of the figure) is on the line EF produced beyond F. The lines A′B′ and C′D′ are approximately circles of radii R/σ, when the central-line is a circle of radius R, and their centres are on the line FE produced beyond E. Thus the neutral plane, and each of the faces that is parallel to it, becomes strained into an anticlastic surface, whose principal curvatures are in the ratio σ : 1. The general appearance of the bent beam is shown in an exaggerated fashion in fig. 11, where the traces of the surface into which the neutral plane is bent are dotted. The result that the ratio of the principal curvatures of the anticlastic surfaces, into which the top and bottom planes of the beam (of rectangular section) are bent, is Poisson’s ratio σ, has been used for the experimental determination of σ. The result that the radius of curvature of the bent central-line is EI/M is used in the experimental determination of E. The quantity EI is often called the “flexural rigidity” of the beam. There are two principal flexural rigidities corresponding to bending in the two principal planes (cf. § 62 below).
 |
| Fig. 12. |
48. That this theory requires modification, when the load does not consist simply of terminal couples, can be seen most easily by considering the problem of a beam loaded at one end with a weight W, and supported in a horizontal position at its other end. The forces that are exerted at any section p, to balance the weight W, must reduce statically to a vertical force W and a couple, and these forces arise from the action of the part Ap on the part Bp (see fig. 12), i.e. from the stresses across the section at p. The couple is equal to the moment of the applied load W about an axis drawn through the centroid of the section p at right angles to the plane of bending. This moment is called the “bending moment” at the section, it is the product of the load W and the distance of the section from the loaded end, so that it varies uniformly along the length of the beam. The stress that suffices in the simpler problem gives rise to no vertical force, and it is clear that in addition to longitudinal tensions and pressures there must be tangential tractions on the cross-sections. The resultant of these tangential tractions must be a force equal to W, and directed vertically; but the direction of the traction at a point of the cross-section need not in general be vertical. The existence of tangential traction on the cross-sections implies the existence of equal tangential traction, directed parallel to the central-line, on some planes or other which are parallel to this line, the two sets of tractions forming a shearing stress. We conclude that such shearing stress is a necessary constituent of the stress-system in the beam bent by terminal transverse load. We can develop a theory of this stress-system from the assumptions (i.) that the tension at any point of the cross-section is related to the bending moment at the section by the same law as in the case of uniform bending by terminal couples; (ii.) that, in addition to this tension, there is at any point shearing stress, involving tangential tractions acting in appropriate directions upon the elements of the cross-sections. When these assumptions are made it appears that there is one and only one distribution of shearing stress by which the conditions of the problem can be satisfied. The determination of the amount and direction of this shearing stress, and of the corresponding strains and displacements, was effected by Saint-Venant and R. F. A. Clebsch for a number of forms of section by means of an analysis of the same kind as that employed in the solution of the torsion problem.
 |
| Fig. 13. |
49. Let l be the length of the beam, x the distance of the section p from the fixed end A, y the distance of any point below the horizontal plane through the centroid of the section at A, then the bending moment at p is W (l − x), and the longitudinal tension P or Xx at any point on the cross-section is −W (l − x)y/I, and this is related to the bending moment exactly as in the simpler problem.
50. The expressions for the shearing stresses depend on the shape of the cross-section. Taking the beam to be of isotropic material and the cross-section to be an ellipse of semiaxes a and b (fig. 13), the a axis being vertical in the unstrained state, and drawing the axis z at right angles to the plane of flexure, we find that the vertical shearing stress U or Xy at any point (y, z) on any cross-section is
| 2W [(a2 − y2) {2a2 (1 + σ) + b2} − z2a2 (1 − 2σ)] | . |
| πa3b (1 + σ) (3a2 + b2) |
The resultant of these stresses is W, but the amount at the centroid, which is the maximum amount, exceeds the average amount, W/πab, in the ratio
If σ = 14, this ratio is 75 for a circle, nearly 43 for a flat elliptic bar with the longest diameter vertical, nearly 85 for a flat elliptic bar with the longest diameter horizontal.
In the same problem the horizontal shearing stress T or Zx at any point on any cross-section is of amount
| − | 4Wyz {a2 (1 + σ) + b2σ} | . |
| πa3b (1 + σ) (3a2 + b2) |
The resultant of these stresses vanishes; but, taking as before σ = 14, and putting for the three cases above a = b, a = 10b, b = 10a, we find that the ratio of the maximum of this stress to the average vertical shearing stress has the values 35, nearly 115, and nearly 4. Thus the stress T is of considerable importance when the beam is a plank.
As another example we may consider a circular tube of external radius r0 and internal radius r1. Writing P, U, T for Xx, Xy, Zx, we find
| P = − | 4W | (l − x)y, |
| π (r04 − r14) |
| U = | W | [ (3 + 2σ) { r02 + r12 − y2 − | r02 r12 | (y2 − z2) } − (1 − 2σ) z2 ] |
| 2(1 + σ) π (r04 − r14) | (y2 + z2)2 |
| T = − | W | { 1 + 2σ + (3 + 2σ) | r02 r12 | } yz; |
| (1 + σ) π (r04 − r14) | (y2 + z2)2 |
and for a tube of radius r and small thickness t the value of P and the maximum values of U and T reduce approximately to
The greatest value of U is in this case approximately twice its average value, but it is possible that these results for the bending of very thin tubes may be seriously at fault if the tube is not plugged, and if the load is not applied in the manner contemplated in the theory (cf. § 55). In such cases the extensions and contractions of the longitudinal filaments may be practically confined to a small part of the material near the ends of the tube, while the rest of the tube is deformed without stretching.
51. The tangential tractions U, T on the cross-sections are necessarily accompanied by tangential tractions on the longitudinal sections, and on each such section the tangential traction is parallel to the central line; on a vertical section z = const. its amount at any point is T, and on a horizontal section y = const. its amount at any point is U.
The internal stress at any point is completely determined by the components P, U, T, but these are not principal stresses (§ 7). Clebsch has given an elegant geometrical construction for determining the principal stresses at any point when the values of P, U, T are known.
 |
| Fig. 14. |
From the point O (fig. 14) draw lines OP, OU, OT, to represent the stresses P, U, T at O, on the cross-section through O, in magnitude, direction and sense, and compound U and T into a resultant represented by OE; the plane EOP is a principal plane of stress at O, and the principal stress at right angles to this plane vanishes. Take M the middle point of OP, and with centre M and radius ME describe a circle cutting the line OP in A and B; then OA and OB represent the magnitudes of the two remaining principal stresses. On AB describe a rectangle ABDC so that DC passes through E; then OC is the direction of the principal stress represented in magnitude by OA, and OD is the direction of the principal stress represented in magnitude by OB.
 |
| Fig. 15. |
52. As regards the strain in the beam, the longitudinal and lateral extensions and contractions depend on the bending moment in the same way as in the simpler problem; but, the bending moment being variable, the anticlastic curvature produced is also variable. In addition to these extensions and contractions there are shearing strains corresponding to the shearing stresses T, U. The shearing strain corresponding to T consists of a relative sliding parallel to the central-line of different longitudinal linear elements combined with a relative sliding in a transverse horizontal direction of elements of different cross-sections; the latter of these is concerned in the production of those displacements by which the variable anticlastic curvature is brought about; to see the effect of the former we may most suitably consider, for the case of an elliptic cross-section, the distortion of the shape of a rectangular portion of a plane of the material which in the natural state was horizontal; all the boundaries of such a portion become parabolas of small curvature, which is variable along the length of the beam, and the particular effect under consideration is the change of the transverse horizontal linear elements from straight lines such as HK to parabolas such as H′K′ (fig. 15); the lines HL and KM are parallel to the central-line, and the figure is drawn for a plane above the neutral plane. When the cross-section is not an ellipse the character of the strain is the same, but the curves are only approximately parabolic.
The shearing strain corresponding to U is a distortion which has the effect that the straight vertical filaments become curved lines which cut the longitudinal filaments obliquely, and thus the cross-sections do not remain plane, but become curved surfaces, and the tangent plane to any one of these surfaces at the centroid cuts the central line obliquely (fig. 16). The angle between these tangent planes and the central-line is the same at all points of the line; and, if it is denoted by 12π + s0, the value of s0 is expressible as
| shearing stress at centroid | , |
| rigidity of material |
and it thus depends on the shape of the cross-section; for the elliptic section of § 50 its value is
| 4W | 2a2 (1 + σ) + b2 | ; | |
| Eπab | 3a2 + b2 |
for a circle (with σ = 14) this becomes 7W / 2Eπa2. The vertical filament through the centroid of any cross-section becomes a cubical parabola, as shown in fig. 16, and the contour lines of the curved surface into which any cross-section is distorted are shown in fig. 17 for a circular section.
 |
| Fig. 16. |
 |
| Fig. 17. |
53. The deflection of the beam is determined from the equation
and the special conditions at the supported end; there is no alteration of this statement on account of the shears. As regards the special condition at an end which is encastrée, or built in, Saint-Venant proposed to assume that the central tangent plane of the cross-section at the end is vertical; with this assumption the tangent to the central line at the end is inclined downwards and makes an angle s0 with the horizontal (see fig. 18); it is, however, improbable that this condition is exactly realized in practice. In the application of the theory to the experimental determination of Young’s modulus, the small angle which the central-line at the support makes with the horizontal is an unknown quantity, to be eliminated by observation of the deflection at two or more points.
54. We may suppose the displacement in a bent beam to be produced by the following operations: (1) the central-line is deflected into its curved form, (2) the cross-sections are rotated about axes through their centroids at right angles to the plane of flexure so as to make angles equal to 12π + s0 with the central-line, (3) each cross-section is distorted in its own plane in such a way that the appropriate variable anticlastic curvature is produced, (4) the cross-sections are further distorted into curved surfaces. The contour lines of fig. 17 show the disturbance from the central tangent plane, not from the original vertical plane.
55. Practical Application of Saint-Venant’s Theory.—The theory above described is exact provided the forces applied to the loaded end, which have W for resultant, are distributed over the terminal section in a particular way, not likely to be realized in practice; and the application to practical problems depends on a principle due to Saint-Venant, to the effect that, except for comparatively small portions of the beam near to the loaded and fixed ends, the resultant only is effective, and its mode of distribution does not seriously affect the internal strain and stress. In fact, the actual stress is that due to forces with the required resultant distributed in the manner contemplated in the theory, superposed upon that due to a certain distribution of forces on each terminal section which, if applied to a rigid body, would keep it in equilibrium; according to Saint-Venant’s principle, the stresses and strains due to such distributions of force are unimportant except near the ends. For this principle to be exactly applicable it is necessary that the length of the beam should be very great compared with any linear dimension of its cross-section; for the practical application it is sufficient that the length should be about ten times the greatest diameter.
56. In recent years the problem of the bending of a beam by loads distributed along its length has been much advanced. It is now practically solved for the case of a load distributed uniformly, or according to any rational algebraic law, and it is also solved for the case where the thickness is small compared with the length and depth, as in a plate girder, and the load is distributed in any way. These solutions are rather complicated and difficult to interpret. The case which has been worked out most fully is that of a transverse load distributed uniformly along the length of the beam. In this case two noteworthy results have been obtained. The first of these is that the central-line in general suffers extension. This result had been found experimentally many years before. In the case of the plate girder loaded uniformly along the top, this extension is just half as great as the extension of the central-line of the same girder when free at the ends, supported along the base, and carrying the same load along the top. The second noteworthy result is that the curvature of the strained central-line is not proportional to the bending moment. Over and above the curvature which would be found from the ordinary relation—
 |
| Fig. 18. |
there is an additional curvature which is the same at all the cross-sections. In ordinary cases, provided the length is large compared with any linear dimension of the cross-section, this additional curvature is small compared with that calculated from the ordinary formula, but it may become important in cases like that of suspension bridges, where a load carried along the middle of the roadway is supported by tensions in rods attached at the sides.
57. When the ordinary relation between the curvature and the bending moment is applied to the calculation of the deflection of continuous beams it must not be forgotten that a correction of the kind just mentioned may possibly be requisite. In the usual method of treating the problem such corrections are not considered, and the ordinary relation is made the basis of the theory. In order to apply this relation to the calculation of the deflection, it is necessary to know the bending moment at every point; and, since the pressures of the supports are not among the data of the problem, we require a method of determining the bending moments at the supports either by calculation or in some other way. The calculation of the bending moment can be replaced by a method of graphical construction, due to Mohr, and depending on the two following theorems:—
(i.) The curve of the central-line of each span of a beam, when the bending moment M is given,[1] is identical with the catenary or funicular curve passing through the ends of the span under a (fictitious) load per unit length of the span equal to M/EI, the horizontal tension in the funicular being unity.
(ii.) The directions of the tangents to this funicular curve at the ends of the span are the same for all statically equivalent systems of (fictitious) load.
When M is known, the magnitude of the resultant shearing stress at any section is dM/dx, where x is measured along the beam.
 |
| Fig. 19. |
58. Let l be the length of a span of a loaded beam (fig. 19), M1 and M2 the bending moments at the ends, M the bending moment at a section distant x from the end (M1), M′ the bending moment at the same section when the same span with the same load is simply supported; then M is given by the formula
| M = M′ + M1 | l − x | + M2 | x | , |
| l | l |
 |
| Fig. 20. |
and thus a fictitious load statically equivalent to M/EI can be easily found when M′ has been found. If we draw a curve (fig. 20) to pass through the ends of the span, so that its ordinate represents the value of M′/EI, the corresponding fictitious loads are statically equivalent to a single load, of amount represented by the area of the curve, placed at the point of the span vertically above the centre of gravity of this area. If PN is the ordinate of this curve, and if at the ends of the span we erect ordinates in the proper sense to represent M1/EI and M2/EI, the bending moment at any point is represented by the length PQ.[2] For a uniformly distributed load the curve of M′ is a parabola M′ = 12wx (l − x), where w is the load per unit of length; and the statically equivalent fictitious load is 112wl3 / EI placed at the middle point G of the span; also the loads statically equivalent to the fictitious loads M1 (l − x) / lEI and M2x / lEI are 12M1l / EI and 12M2l / EI placed at the points g, g′ of trisection of the span. The funicular polygon for the fictitious loads can thus be drawn, and the direction of the central-line at the supports is determined when the bending moments at the supports are known.
 |
| Fig. 21. |
 |
| Fig. 22. |
 |
| Fig. 23. |
59. When there is more than one span the funiculars in question may be drawn for each of the spans, and, if the bending moments at the ends of the extreme spans are known, the intermediate ones can be determined. This determination depends on two considerations: (1) the fictitious loads corresponding to the bending moment at any support are proportional to the lengths of the spans which abut on that support; (2) the sides of two funiculars that end at any support coincide in direction. Fig. 21 illustrates the method for the case of a uniform beam on three supports A, B, C, the ends A and C being freely supported. There will be an unknown bending moment M0 at B, and the system[3] of fictitious loads is 112wAB3/EI at G the middle point of AB, 112wBC3 / EI at G′ the middle point of BC, −12M0AB / EI at g and −12M0BC / EI at g′, where g and g′ are the points of trisection nearer to B of the spans AB, BC. The centre of gravity of the two latter is a fixed point independent of M0, and the line VK of the figure is the vertical through this point. We draw AD and CE to represent the loads at G and G′ in magnitude; then D and E are fixed points. We construct any triangle UVW whose sides UV, UW pass through D, B, and whose vertices lie on the verticals gU, VK, g′W; the point F where VW meets DB is a fixed point, and the lines EF, DK are the two sides (2, 4) of the required funiculars which do not pass through A, B or C. The remaining sides (1, 3, 5) can then be drawn, and the side 3 necessarily passes through B; for the triangle UVW and the triangle whose sides are 2, 3, 4 are in perspective.
The bending moment M0 is represented in the figure by the vertical line BH where H is on the continuation of the side 4, the scale being given by
| BH | = | 12M0BC | ; |
| CE | 112wBC3 |
this appears from the diagrams of forces, fig. 22, in which the oblique lines are marked to correspond to the sides of the funiculars to which they are parallel.
In the application of the method to more complicated cases there are two systems of fixed points corresponding to F, by means of which the sides of the funiculars are drawn.
60. Finite Bending of Thin Rod.—The equation
may also be applied to the problem of the flexure in a principal plane of a very thin rod or wire, for which the curvature need not be small. When the forces that produce the flexure are applied at the ends only, the curve into which the central-line is bent is one of a definite family of curves, to which the name elastica has been given, and there is a division of the family into two species according as the external forces are applied directly to the ends or are applied to rigid arms attached to the ends; the curves of the former species are characterized by the presence of inflections at all the points at which they cut the line of action of the applied forces.
We select this case for consideration. The problem of determining the form of the curve (cf. fig. 23) is mathematically identical with the problem of determining the motion of a simple circular pendulum oscillating through a finite angle, as is seen by comparing the differential equation of the curve
| EI | d2φ | + W sin φ = 0 |
| ds2 |
with the equation of motion of the pendulum
| l | d2φ | + g sin φ = 0. |
| dt2 |
The length L of the curve between two inflections corresponds to the time of oscillation of the pendulum from rest to rest, and we thus have
L √(W/EI) = 2K,
 |
| Fig. 24. |
where K is the real quarter period of elliptic functions of modulus sin 12α, and α is the angle at which the curve cuts the line of action of the applied forces. Unless the length of the rod exceeds π√(EI/W) it will not bend under the force, but when the length is great enough there may be more than two points of inflection and more than one bay of the curve; for n bays (n + 1 inflections) the length must exceed nπ √(EI/W). Some of the forms of the curve are shown in fig. 24.
For the form d, in which two bays make a figure of eight, we have
L√(W/EI) = 4.6, α = 130°
approximately. It is noteworthy that whenever the length and force admit of a sinuous form, such as α or b, with more than two inflections, there is also possible a crossed form, like e, with two inflections only; the latter form is stable and the former unstable.
 |
| Fig. 25. |
61. The particular case of the above for which α is very small is a curve of sines of small amplitude, and the result in this case has been applied to the problem of the buckling of struts under thrust. When the strut, of length L′, is maintained upright at its lower end, and loaded at its upper end, it is simply contracted, unless L′2W > 14π2EI, for the lower end corresponds to a point at which the tangent is vertical on an elastica for which the line of inflections is also vertical, and thus the length must be half of one bay (fig. 25, a). For greater lengths or loads the strut tends to bend or buckle under the load. For a very slight excess of L′2W above 14π2EI, the theory on which the above discussion is founded, is not quite adequate, as it assumes the central-line of the strut to be free from extension or contraction, and it is probable that bending without extension does not take place when the length or the force exceeds the critical value but slightly. It should be noted also that the formula has no application to short struts, as the theory from which it is derived is founded on the assumption that the length is great compared with the diameter (cf. § 56).
The condition of buckling, corresponding to the above, for a long strut, of length L′, when both ends are free to turn is L′2W > π2EI; for the central-line forms a complete bay (fig. 25, b); if both ends are maintained in the same vertical line, the condition is L′2W > 4π2EI, the central-line forming a complete bay and two half bays (fig. 25, c).
62. In our consideration of flexure it has so far been supposed that the bending takes place in a principal plane. We may remove this restriction by resolving the forces that tend to produce bending into systems of forces acting in the two principal planes. To each plane there corresponds a particular flexural rigidity, and the systems of forces in the two planes give rise to independent systems of stress, strain and displacement, which must be superposed in order to obtain the actual state. Applying this process to the problem of §§ 48-54, and supposing that one principal axis of a cross-section at its centroid makes an angle θ with the vertical, then for any shape of section the neutral surface or locus of unextended fibres cuts the section in a line DD′, which is conjugate to the vertical diameter CP with respect to any ellipse of inertia of the section. The central-line is bent into a plane curve which is not in a vertical plane, but is in a plane through the line CY which is perpendicular to DD′ (fig. 26).
 |
| Fig. 26. |
63. Bending and Twisting of Thin Rods.—When a very thin rod or wire is bent and twisted by applied forces, the forces on any part of it limited by a normal section are balanced by the tractions across the section, and these tractions are statically equivalent to certain forces and couples at the centroid of the section; we shall call them the stress-resultants and the stress-couples. The stress-couples consist of two flexural couples in the two principal planes, and the torsional couple about the tangent to the central-line. The torsional couple is the product of the torsional rigidity and the twist produced; the torsional rigidity is exactly the same as for a straight rod of the same material and section twisted without bending, as in Saint-Venant’s torsion problem (§ 42). The twist τ is connected with the deformation of the wire in this way: if we suppose a very small ring which fits the cross-section of the wire to be provided with a pointer in the direction of one principal axis of the section at its centroid, and to move along the wire with velocity v, the pointer will rotate about the central-line with angular velocity τv. The amount of the flexural couple for either principal plane at any section is the product of the flexural rigidity for that plane, and the resolved part in that plane of the curvature of the central line at the centroid of the section; the resolved part of the curvature along the normal to any plane is obtained by treating the curvature as a vector directed along the normal to the osculating plane and projecting this vector. The flexural couples reduce to a single couple in the osculating plane proportional to the curvature when the two flexural rigidities are equal, and in this case only.
The stress-resultants across any section are tangential forces in the two principal planes, and a tension or thrust along the central-line; when the stress-couples and the applied forces are known these stress-resultants are determinate. The existence, in particular, of the resultant tension or thrust parallel to the central-line does not imply sensible extension or contraction of the central filament, and the tension per unit area of the cross-section to which it would be equivalent is small compared with the tensions and pressures in longitudinal filaments not passing through the centroid of the section; the moments of the latter tensions and pressures constitute the flexural couples.
 |
| Fig. 27. |
64. We consider, in particular, the case of a naturally straight spring or rod of circular section, radius c, and of homogeneous isotropic material. The torsional rigidity is 14Eπc4 / (1 + σ); and the flexural rigidity, which is the same for all planes through the central-line, is 14Eπc4; we shall denote these by C and A respectively. The rod may be held bent by suitable forces into a curve of double curvature with an amount of twist τ, and then the torsional couple is Cτ, and the flexural couple in the osculating plane is A/ρ, where ρ is the radius of circular curvature. Among the curves in which the rod can be held by forces and couples applied at its ends only, one is a circular helix; and then the applied forces and couples are equivalent to a wrench about the axis of the helix.
Let α be the angle and r the radius of the helix, so that ρ is r sec2α; and let R and K be the force and couple of the wrench (fig. 27).
Then the couple formed by R and an equal and opposite force at any section and the couple K are equivalent to the torsional and flexural couples at the section, and this gives the equations for R and K
| R = A | sin α cos3 α | − | cos α | , |
| r2 | r |
| K = A | cos3 α | + Cτ sin α. |
| r |
The thrust across any section is R sin α parallel to the tangent to the helix, and the shearing stress-resultant is R cos α at right angles to the osculating plane.
When the twist is such that, if the rod were simply unbent, it would also be untwisted, τ is (sin α cos α) / r, and then, restoring the values of A and C, we have
| R = | Eπc4 | σ | sin α cos2 α, | |
| 4r 2 | 1 + σ |
| K = | Eπc4 | 1 + σ cos2 α | cos α. | |
| 4r | 1 + σ |
65. The theory of spiral springs affords an application of these results. The stress-couples called into play when a naturally helical spring (α, r) is held in the form of a helix (α′, r ′), are equal to the differences between those called into play when a straight rod of the same material and section is held in the first form, and those called into play when it is held in the second form.
Thus the torsional couple is
| C ( | sin α′ cos α′ | − | sin α cos α | ). |
| r ′ | r |
and the flexural couple is
| A ( | cos2 α′ | − | cos2 α | ). |
| r ′ | r |
The wrench (R, K) along the axis by which the spring can be held in the form (α′, r ′) is given by the equations
| R = A | sin α′ | ( | cos2 α′ | − | cos2 α | ) − C | cos α′ | ( | sin α′ cos α′ | − | sin α cos α | ), |
| r ′ | r ′ | r | r ′ | r ′ | r |
| K = A cos α′ ( | cos2 α′ | − | cos2 α | ) + sin α′ ( | sin α′ cos α′ | − | sin α cos α | ). |
| r ′ | r | r ′ | r |
When the spring is slightly extended by an axial force F, = −R, and there is no couple, so that K vanishes, and α′, r ′ differ very little from α, r, it follows from these equations that the axial elongation, δx, is connected with the axial length x and the force F by the equation
| F = | Eπc4 | sin α | δx | , | ||
| 4r 2 | 1 + σ cos2 α | x |
and that the loaded end is rotated about the axis of the helix through a small angle
| 4σFxr cos α | , |
| Eπc4 |
the sense of the rotation being such that the spring becomes more tightly coiled.
66. A horizontal pointer attached to a vertical spiral spring would be made to rotate by loading the spring, and the angle through which it turns might be used to measure the load, at any rate, when the load is not too great; but a much more sensitive contrivance is the twisted strip devised by W. E. Ayrton and J. Perry. A very thin, narrow rectangular strip of metal is given a permanent twist about its longitudinal middle line, and a pointer is attached to it at right angles to this line. When the strip is subjected to longitudinal tension the pointer rotates through a considerable angle. G. H. Bryan (Phil. Mag., December 1890) has succeeded in constructing a theory of the action of the strip, according to which it is regarded as a strip of plating in the form of a right helicoid, which, after extension of the middle line, becomes a portion of a slightly different helicoid; on account of the thinness of the strip, the change of curvature of the surface is considerable, even when the extension is small, and the pointer turns with the generators of the helicoid.
If b stands for the breadth and t for the thickness of the strip, and τ for the permanent twist, the approximate formula for the angle θ through which the strip is untwisted on the application of a load W was found to be
| θ = | Wbτ (1 + σ) | . | ||||
| 2Et 3 ( 1 + | (1 + σ) | b4τ2 | ) | |||
| 30 | t 2 | |||||
The quantity bτ which occurs in the formula is the total twist in a length of the strip equal to its breadth, and this will generally be very small; if it is small of the same order as t/b, or a higher order, the formula becomes 12Wbτ (1+σ) / Et 3, with sufficient approximation, and this result appears to be in agreement with observations of the behaviour of such strips.
67. Thin Plate under Pressure.—The theory of the deformation of plates, whether plane or curved, is very intricate, partly because of the complexity of the kinematical relations involved. We shall here indicate the nature of the effects produced in a thin plane plate, of isotropic material, which is slightly bent by pressure. This theory should have an application to the stress produced in a ship’s plates. In the problem of the cylinder under internal pressure (§ 77 below) the most important stress is the circumferential tension, counteracting the tendency of the circular filaments to expand under the pressure; but in the problem of a plane plate some of the filaments parallel to the plane of the plate are extended and others are contracted, so that the tensions and pressures along them give rise to resultant couples but not always to resultant forces. Whatever forces are applied to bend the plate, these couples are always expressible, at least approximately in terms of the principal curvatures produced in the surface which, before strain, was the middle plane of the plate. The simplest case is that of a rectangular plate, bent by a distribution of couples applied to its edges, so that the middle surface becomes a cylinder of large radius R; the requisite couple per unit of length of the straight edges is of amount C/R, where C is a certain constant; and the requisite couple per unit of length of the circular edges is of amount Cσ/R, the latter being required to resist the tendency to anticlastic curvature (cf. § 47). If normal sections of the plate are supposed drawn through the generators and circular sections of the cylinder, the action of the neighbouring portions on any portion so bounded involves flexural couples of the above amounts. When the plate is bent in any manner, the curvature produced at each section of the middle surface may be regarded as arising from the superposition of two cylindrical curvatures; and the flexural couples across normal sections through the lines of curvature, estimated per unit of length of those lines, are C (1/R1 + σ/R2) and C (1/R2 + σ/R1), where R1 and R2 are the principal radii of curvature. The value of C for a plate of small thickness 2h is 23Eh3 / (1 − σ2). Exactly as in the problem of the beam (§§ 48, 56), the action between neighbouring portions of the plate generally involves shearing stresses across normal sections as well as flexural couples; and the resultants of these stresses are determined by the conditions that, with the flexural couples, they balance the forces applied to bend the plate.
 |
| Fig. 28. |
68. To express this theory analytically, let the middle plane of the plate in the unstrained position be taken as the plane of (x, y), and let normal sections at right angles to the axes of x and y be drawn through any point. After strain let w be the displacement of this point in the direction perpendicular to the plane, marked p in fig. 28. If the axes of x and y were parallel to the lines of curvature at the point, the flexural couple acting across the section normal to x (or y) would have the axis of y (or x) for its axis; but when the lines of curvature are inclined to the axes of co-ordinates, the flexural couple across a section normal to either axis has a component about that axis as well as a component about the perpendicular axis. Consider an element ABCD of the section at right angles to the axis of x, contained between two lines near together and perpendicular to the middle plane. The action of the portion of the plate to the right upon the portion to the left, across the element, gives rise to a couple about the middle line (y) of amount, estimated per unit of length of that line, equal to C (∂2w∂x2 + σ ∂2w∂y2), = G1, say, and to a couple, similarly estimated, about the normal (x) of amount −C (1 − σ) ∂2w∂x∂y, H, say. The corresponding couples on an element of a section at right angles to the axis of y, estimated per unit of length of the axis of x, are of amounts −C (∂2w∂y2 + σ ∂2w∂x2), = G2 say, and −H. The resultant S1 of the shearing stresses on the element ABCD, estimated as before, is given by the equation S1 = ∂G1∂x − ∂H∂y (cf. § 57), and the corresponding resultant S2 for an element perpendicular to the axis of y is given by the equation S2= −∂H∂x − ∂G2∂y. If the plate is bent by a pressure p per unit of area, the equation of equilibrium is ∂S1∂x + ∂S2∂y = p, or, in terms of w,
| ∂4w | + | ∂4w | + 2 | ∂4w | = | p | . |
| ∂x4 | ∂y4 | ∂x2∂y2 | C |
This equation, together with the special conditions at the rim, suffices for the determination of w, and then all the quantities here introduced are determined. Further, the most important of the stress-components are those which act across elements of normal sections: the tension in direction x, at a distance z from the middle plane measured in the direction of p, is of amount −3Cz2h3 (∂2w∂x3 + σ(∂2w∂y2), and there is a corresponding tension in direction y; the shearing stress consisting of traction parallel to y on planes x = const., and traction parallel to x on planes y = const., is of amount 3C(1 − σ)z2h3 ∂2w∂x∂y; these tensions and shearing stresses are equivalent to two principal tensions, in the directions of the lines of curvature of the surface into which the middle plane is bent, and they give rise to the flexural couples.
69. In the special example of a circular plate, of radius a, supported at the rim, and held bent by a uniform pressure p, the value of w at a point distant r from the axis is
| 1 p | (a2 − r 2) ( | 5 + σ | a2 − r 2 ), |
| 64 C | 1 + σ |
and the most important of the stress components is the radial tension, of which the amount at any point is 332(3 + σ) pz (a2 − r)/h3; the maximum radial tension is about 13(a/h)2p, and, when the thickness is small compared with the diameter, this is a large multiple of p.
70. General Theorems.—Passing now from these questions of flexure and torsion, we consider some results that can be deduced from the general equations of equilibrium of an elastic solid body.
 |
| Fig. 29. |
The form of the general expression for the potential energy (§ 27) stored up in the strained body leads, by a general property of quadratic functions, to a reciprocal theorem relating to the effects produced in the body by two different systems of forces, viz.: The whole work done by the forces of the first system, acting over the displacements produced by the forces of the second system, is equal to the whole work done by the forces of the second system, acting over the displacements produced by the forces of the first system. By a suitable choice of the second system of forces, the average values of the component stresses and strains produced by given forces, considered as constituting the first system, can be obtained, even when the distribution of the stress and strain cannot be determined.
Taking for example the problem presented by an isotropic body of any form[4] pressed between two parallel planes distant l apart (fig. 29), and denoting the resultant pressure by p, we find that the diminution of volume -δv is given by the equation
where k is the modulus of compression, equal to 13E / (1 − 2σ). Again, take the problem of the changes produced in a heavy body by different ways of supporting it; when the body is suspended from one or more points in a horizontal plane its volume is increased by
where W is the weight of the body, and h the depth of its centre of gravity below the plane; when the body is supported by upward vertical pressures at one or more points in a horizontal plane the volume is diminished by
where h′ is the height of the centre of gravity above the plane; if the body is a cylinder, of length l and section A, standing with its base on a smooth horizontal plane, its length is shortened by an amount
if the same cylinder lies on the plane with its generators horizontal, its length is increased by an amount
71. In recent years important results have been found by considering the effects produced in an elastic solid by forces applied at isolated points.
Taking the case of a single force F applied at a point in the interior, we may show that the stress at a distance r from the point consists of
(1) a radial pressure of amount
| 2 − σ | F | cos θ | , | ||
| 1 − σ | 4π | r 2 |
(2) tension in all directions at right angles to the radius of amount
| 1 − 2σ | F | cos θ | , | ||
| 2(1 − σ) | 4π | r 2 |
(3) shearing stress consisting of traction acting along the radius dr on the surface of the cone θ = const. and traction acting along the meridian dθ on the surface of the sphere r = const. of amount
| 1 − 2σ | F | sin θ | , | ||
| 2(1 − σ) | 4π | r 2 |
where θ is the angle between the radius vector r and the line of action of F. The line marked T in fig. 30 shows the direction of the tangential traction on the spherical surface.
 |
| Fig. 30. |
 |
| Fig. 31. |
Thus the lines of stress are in and perpendicular to the meridian plane, and the direction of one of those in the meridian plane is inclined to the radius vector r at an angle
| 12 tan−1 ( | 2 − 4σ | tan θ ). |
| 5 − 4σ |
The corresponding displacement at any point is compounded of a radial displacement of amount
| 1 + σ | F | cos θ | ||
| 2(1 − σ) | 4πE | r |
and a displacement parallel to the line of action of F of amount
| (3 − 4σ) (1 + σ) | F | 1 | . | ||
| 2(1 − σ) | 4πE | r |
The effects of forces applied at different points and in different directions can be obtained by summation, and the effect of continuously distributed forces can be obtained by integration.
72. The stress system considered in § 71 is equivalent, on the plane through the origin at right angles to the line of action of F, to a resultant pressure of magnitude 12F at the origin and a radical traction of amount 1 − 2σ2(1 − σ) F4πr 2, and, by the application of this system of tractions to a solid bounded by a plane, the displacement just described would be produced. There is also another stress system for a solid so bounded which is equivalent, on the same plane, to a resultant pressure at the origin, and a radial traction proportional to 1/r 2, but these are in the ratio 2π : r −2, instead of being in the ratio 4π(1 − σ) : (1 − 2σ)r −2.
The second stress system (see fig. 31) consists of:
(1) radial pressure F′r −2,
(2) tension in the meridian plane across the radius vector of amount
(3) tension across the meridian plane of amount
(4) shearing stress as in § 71 of amount
and the stress across the plane boundary consists of a resultant pressure of magnitude 2πF′ and a radial traction of amount F′r −2. If then we superpose the component stresses of the last section multiplied by 4(1 − σ)W/F, and the component stresses here written down multiplied by −(1 − 2σ)W/2πF′, the stress on the plane boundary will reduce to a single pressure W at the origin. We shall thus obtain the stress system at any point due to such a force applied at one point of the boundary.
In the stress system thus arrived at the traction across any plane parallel to the boundary is directed away from the place where W is supported, and its amount is 3W cos2θ / 2πr2. The corresponding displacement consists of
(1) a horizontal displacement radially outwards from the vertical through the origin of amount
| W (1 + σ) sin θ | ( cos θ − | 1 − 2σ | ), |
| 2πEr | 1 + cos θ |
(2) a vertical displacement downwards of amount
| W (1 + σ) | {2 (1 − σ) + cos2θ }. |
| 2πEr |
The effects produced by a system of loads on a solid bounded by a plane can be deduced.
The results for a solid body bounded by an infinite plane may be interpreted as giving the local effects of forces applied to a small part of the surface of a body. The results show that pressure is transmitted into a body from the boundary in such a way that the traction at a point on a section parallel to the boundary is the same at all points of any sphere which touches the boundary at the point of pressure, and that its amount at any point is inversely proportional to the square of the radius of this sphere, while its direction is that of a line drawn from the point of pressure to the point at which the traction is estimated. The transmission of force through a solid body indicated by this result was strikingly demonstrated in an attempt that was made to measure the lunar deflexion of gravity; it was found that the weight of the observer on the floor of the laboratory produced a disturbance of the instrument sufficient to disguise completely the effect which the instrument had been designed to measure (see G. H. Darwin, The Tides and Kindred Phenomena in the Solar System, London, 1898).
73. There is a corresponding theory of two-dimensional systems, that is to say, systems in which either the displacement is parallel to a fixed plane, or there is no traction across any plane of a system of parallel planes. This theory shows that, when pressure is applied at a point of the edge of a plate in any direction in the plane of the plate, the stress developed in the plate consists exclusively of radial pressure across any circle having the point of pressure as centre, and the magnitude of this pressure is the same at all points of any circle which touches the edge at the point of pressure, and its amount at any point is inversely proportional to the radius of this circle. This result leads to a number of interesting solutions of problems relating to plane systems; among these may be mentioned the problem of a circular plate strained by any forces applied at its edge.
74. The results stated in § 72 have been applied to give an account of the nature of the actions concerned in the impact of two solid bodies. The dissipation of energy involved in the impact is neglected, and the resultant pressure between the bodies at any instant during the impact is equal to the rate of destruction of momentum of either along the normal to the plane of contact drawn towards the interior of the other. It has been shown that in general the bodies come into contact over a small area bounded by an ellipse, and remain in contact for a time which varies inversely as the fifth root of the initial relative velocity.
For equal spheres of the same material, with σ = 14, impinging directly with relative velocity v, the patches that come into contact are circles of radius
| ( | 45π | ) | 15 | ( | v | ) | 25 | r, |
| 256 | V |
where r is the radius of either, and V the velocity of longitudinal waves in a thin bar of the material. The duration of the impact is approximately
| (2.9432) ( | 2025π2 | ) | 1/5 | r | . |
| 512 | v1/5V4/5 |
For two steel spheres of the size of the earth impinging with a velocity of 1 cm. per second the duration of the impact would be about twenty-seven hours. The fact that the duration of impact is, for moderate velocities, a considerable multiple of the time taken by a wave of compression to travel through either of two impinging bodies has been ascertained experimentally, and constitutes the reason for the adequacy of the statical theory here described.
75. Spheres and Cylinders.—Simple results can be found for spherical and cylindrical bodies strained by radial forces.
For a sphere of radius a, and of homogeneous isotropic material of density ρ, strained by the mutual gravitation of its parts, the stress at a distance r from the centre consists of
(1) uniform hydrostatic pressure of amount 110 gρa (3 − σ) / (1 − σ),
(2) radial tension of amount 110 gρ (r2/a) (3 − σ) / (1 − σ),
(3) uniform tension at right angles to the radius vector of amount
110 gρ (r2/a) (1 + 3σ) / (1 − σ),
where g is the value of gravity at the surface. The corresponding strains consist of
(1) uniform contraction of all lines of the body of amount
130 k−1gρa (3 − σ) / (1 − σ),
(2) radial extension of amount 110 k−1gρ (r2/a) (1 + σ) / (1 − σ),
(3) extension in any direction at right angles to the radius vector of amount
130 k−1gρ (r2/a) (1 + σ) / (1 − σ),
where k is the modulus of compression. The volume is diminished by the fraction gρa/5k of itself. The parts of the radii vectors within the sphere r = a {(3 − σ) / (3 + 3σ)}1/2 are contracted, and the parts without this sphere are extended. The application of the above results to the state of the interior of the earth involves a neglect of the caution emphasized in § 40, viz. that the strain determined by the solution must be small if the solution is to be accepted. In a body of the size and mass of the earth, and having a resistance to compression and a rigidity equal to those of steel, the radial contraction at the centre, as given by the above solution, would be nearly 13, and the radial extension at the surface nearly 16, and these fractions can by no means be regarded as “small.”
76. In a spherical shell of homogeneous isotropic material, of internal radius r1 and external radius r0, subjected to pressure p0 on the outer surface, and p1 on the inner surface, the stress at any point distant r from the centre consists of
(1) uniform tension in all directions of amount p1r13 − p0r03r03 − r13,
(2) radial pressure of amount p1 − p0r03 − r13 r03r13r3,
(3) tension in all directions at right angles to the radius vector of amount
| 12 | p1 − p0 | r03r13 | . | |
| r03 − r13 | r3 |
The corresponding strains consist of
(1) uniform extension of all lines of the body of amount
| 1 | p1r13 − p0r03 | , | |
| 3k | r03 − r13 |
(2) radial contraction of amount
| 1 | p1 − p0 | r03r13 | , | ||
| 2μ | r03 − r13 | r3 |
(3) extension in all directions at right angles to the radius vector of amount
| 1 | p1 − p0 | r03r13 | , | ||
| 4μ | r03 − r13 | r3 |
where μ is the modulus of rigidity of the material, = 12E / (1 + σ). The volume included between the two surfaces of the body is increased by the fraction p1r13 − p0r03)k(r03 − r13) of itself, and the volume within the inner surface is increased by the fraction
| 3 (p1 − p0) | r03 | + | p1r13 − p0r03 | |
| 4μ | r03 − r13 | k (r03 − r13) |
of itself. For a shell subject only to internal pressure p the greatest extension is the extension at right angles to the radius at the inner surface, and its amount is
| pr13 | ( | 1 | + | 1 | r03 | ); | |
| r03 − r13 | 3k | 4μ | r13 |
the greatest tension is the transverse tension at the inner surface, and its amount is p (12 r03 + r13) / (r03 − r13).
77. In the problem of a cylindrical shell under pressure a complication may arise from the effects of the ends; but when the ends are free from stress the solution is very simple. With notation similar to that in § 76 it can be shown that the stress at a distance r from the axis consists of
(1) uniform tension in all directions at right angles to the axis of amount
| p1r12 − p0r02 | , |
| r02 − r12 |
| (2) radial pressure of amount | p1 − p0 | r02r12 | , | |
| r02 − r12 | r2 |
(3) hoop tension numerically equal to this radial pressure.
The corresponding strains consist of
(1) uniform extension of all lines of the material at right angles to the axis of amount
| 1 − σ | p1r 12 − p0r 02 | , | |
| E | r 02 − r 12 |
(2) radial contraction of amount
| 1 + σ | p1 − p0 | r 02r 12 | , | ||
| E | r 02 − r 12 | r 2 |
(3) extension along the circular filaments numerically equal to this radial contraction,
(4) uniform contraction of the longitudinal filaments of amount
| 2σ | p1r 12 − p0r 02 | . | |
| E | r 02 − r 12 |
For a shell subject only to internal pressure p the greatest extension is the circumferential extension at the inner surface, and its amount is
| p | ( | r 02 + r 12 | + σ ); |
| E | r 02 − r 12 |
the greatest tension is the hoop tension at the inner surface, and its amount is p (r 02 + r 12) / (r 02 − r 12).
78. When the ends of the tube, instead of being free, are closed by disks, so that the tube becomes a closed cylindrical vessel, the longitudinal extension is determined by the condition that the resultant longitudinal tension in the walls balances the resultant normal pressure on either end. This condition gives the value of the extension of the longitudinal filaments as
(p1r 12 − p0r 02) / 3k (r 02 − r 12),
where k is the modulus of compression of the material. The result may be applied to the experimental determination of k, by measuring the increase of length of a tube subjected to internal pressure (A. Mallock, Proc. R. Soc. London, lxxiv., 1904, and C. Chree, ibid.).
79. The results obtained in § 77 have been applied to gun construction; we may consider that one cylinder is heated so as to slip over another upon which it shrinks by cooling, so that the two form a single body in a condition of initial stress.
We take P as the measure of the pressure between the two, and p for the pressure within the inner cylinder by which the system is afterwards strained, and denote by r ′ the radius of the common surface. To obtain the stress at any point we superpose the system consisting of radial pressure p (r 12/r 2) · (r 02 − r 2) / (r 02 − r 12) and hoop tension p (r 12/r 2) · (r 02 + r 2) / (r 02 − r 12) upon a system which, for the outer cylinder, consists of radial pressure P (r ′2/r 2) · (r 02 − r 2) / (r 02 − r ′2) and hoop tension P (r ′2/r 2) · (r 02 + r 2) / (r 02 − r ′2), and for the inner cylinder consists of radial pressure P (r ′2/r 2) · (r 2 − r 12) / (r ′2 − r 12) and hoop tension P (r ′2/r 2) · (r 2 + r 12) / (r ′2 − r 12). The hoop tension at the inner surface is less than it would be for a tube of equal thickness without initial stress in the ratio
| 1 − | P | 2r ′2 | r 02 + r 12 | : 1. | ||
| p | r 02 + r 12 | r ′2 − r 12 |
This shows how the strength of the tube is increased by the initial stress. When the initial stress is produced by tightly wound wire, a similar gain of strength accrues.
80. In the problem of determining the distribution of stress and strain in a circular cylinder, rotating about its axis, simple solutions have been obtained which are sufficiently exact for the two special cases of a thin disk and a long shaft.
Suppose that a circular disk of radius a and thickness 2l, and of density ρ, rotates about its axis with angular velocity ω, and consider the following systems of superposed stresses at any point distant r from the axis and z from the middle plane:
(1) uniform tension in all directions at right angles to the axis of amount 18 ω2ρa2 (3 + σ),
(2) radial pressure of amount 18 ω2ρr 2 (3 + σ),
(3) pressure along the circular filaments of amount 18 ω2ρr 2 (1 + 3σ),
(4) uniform tension in all directions at right angles to the axis of amount 16 ω2ρ (l2 − 3z2) σ (1 + σ) / (1 − σ).
The corresponding strains may be expressed as
(1) uniform extension of all filaments at right angles to the axis of amount
| 1 − σ | 18 ω2ρa2 (3 + σ), |
| E |
(2) radial contraction of amount
| 1 − σ2 | 38 ω2ρr 2, |
| E |
(3) contraction along the circular filaments of amount
| 1 − σ2 | 18 ω2ρr 2, |
| E |
(4) extension of all filaments at right angles to the axis of amount
| 1 | 16 ω2ρ (l2 − 3z2) σ (1 + σ), |
| E |
(5) contraction of the filaments normal to the plane of the disk of amount
| 2σ | 18 ω2ρa2 (3 + σ) − | σ | 12 ω2ρr 2 (1 + σ) + | 2σ | 16 ω2ρ (l2 − 3z2) σ | (1 + σ) | . |
| E | E | E | (1 − σ) |
The greatest extension is the circumferential extension near the centre, and its amount is
| (3 + σ) (1 − σ) | ω2ρa2 + | σ (1 + σ) | ω2ρl2. |
| 8E | 6E |
 |
| Fig. 32. |
The longitudinal contraction is required to make the plane faces of the disk free from pressure, and the terms in l and z enable us to avoid tangential traction on any cylindrical surface. The system of stresses and strains thus expressed satisfies all the conditions, except that there is a small radial tension on the bounding surface of amount per unit area 16 ω2ρ (l2 − 3z2) σ (1 + σ) / (1 − σ). The resultant of these tensions on any part of the edge of the disk vanishes, and the stress in question is very small in comparison with the other stresses involved when the disk is thin; we may conclude that, for a thin disk, the expressions given represent the actual condition at all points which are not very close to the edge (cf. § 55). The effect to the longitudinal contraction is that the plane faces become slightly concave (fig. 32).
81. The corresponding solution for a disk with a circular axle-hole (radius b) will be obtained from that given in the last section by superposing the following system of additional stresses:
(1) radial tension of amount 18 ω2ρb2 (1 − a2/r 2) (3 + σ),
(2) tension along the circular filaments of amount
18 ω2ρb2 (1 + a2/r 2) (3 + σ).
The corresponding additional strains are
(1) radial contraction of amount
| 3 + σ | { (1 + σ) | a2 | − (1 − σ) } ω2ρb2, |
| 8E | r 2 |
(2) extension along the circular filaments of amount
| 3 + σ | { (1 + σ) | a2 | + (1 − σ) } ω2ρb2. |
| 8E | r 2 |
(3) contraction of the filaments parallel to the axis of amount
| σ (3 + σ) | ω2ρb2. |
| 4E |
Again, the greatest extension is the circumferential extension at the inner surface, and, when the hole is very small, its amount is nearly double what it would be for a complete disk.
82. In the problem of the rotating shaft we have the following stress-system:
(1) radial tension of amount 18 ω2ρ (a2 − r 2) (3 − 2σ) / (1 − σ),
(2) circumferential tension of amount 18 ω2ρ {a2 (3 − 2σ) / (1 − σ) − r 2 (1 + 2σ) / (1 − σ)},
(3) longitudinal tension of amount 14 ω2ρ (a2 − 2r 2) σ / (1 − σ).
The resultant longitudinal tension at any normal section vanishes, and the radial tension vanishes at the bounding surface; and thus the expressions here given may be taken to represent the actual condition at all points which are not very close to the ends of the shaft. The contraction of the longitudinal filaments is uniform and equal to 12 ω2ρa2σ / E. The greatest extension in the rotating shaft is the circumferential extension close to the axis, and its amount is 18 ω2ρa2 (3 − 5σ) / E (1 − σ).
The value of any theory of the strength of long rotating shafts founded on these formulae is diminished by the circumstance that at sufficiently high speeds the shaft may tend to take up a curved form, the straight form being unstable. The shaft is then said to whirl. This occurs when the period of rotation of the shaft is very nearly coincident with one of its periods of lateral vibration. The lowest speed at which whirling can take place in a shaft of length l, freely supported at its ends, is given by the formula
ω2ρ = 14 Ea2 (π/l)4.
As in § 61, this formula should not be applied unless the length of the shaft is a considerable multiple of its diameter. It implies that whirling is to be expected whenever ω approaches this critical value.
83. When the forces acting upon a spherical or cylindrical body are not radial, the problem becomes more complicated. In the case of the sphere deformed by any forces it has been completely solved, and the solution has been applied by Lord Kelvin and Sir G. H. Darwin to many interesting questions of cosmical physics. The nature of the stress produced in the interior of the earth by the weight of continents and mountains, the spheroidal figure of a rotating solid planet, the rigidity of the earth, are among the questions which have in this way been attacked. Darwin concluded from his investigation that, to support the weight of the existing continents and mountain ranges, the materials of which the earth is composed must, at great depths (1600 kilometres), have at least the strength of granite. Kelvin concluded from his investigation that the actual heights of the tides in the existing oceans can be accounted for only on the supposition that the interior of the earth is solid, and of rigidity nearly as great as, if not greater than, that of steel.
84. Some interesting problems relating to the strains produced in a cylinder of finite length by forces distributed symmetrically round the axis have been solved. The most important is that of a cylinder crushed between parallel planes in contact with its plane ends. The solution was applied to explain the discrepancies that have been observed in different tests of crushing strength according as the ends of the test specimen are or are not prevented from spreading. It was applied also to explain the fact that in such tests small conical pieces are sometimes cut out at the ends subjected to pressure.
85. Vibrations and Waves.—When a solid body is struck, or otherwise suddenly disturbed, it is thrown into a state of vibration. There always exist dissipative forces which tend to destroy the vibratory motion, one cause of the subsidence of the motion being the communication of energy to surrounding bodies. When these dissipative forces are disregarded, it is found that an elastic solid body is capable of vibrating in such a way that the motion of any particle is simple harmonic motion, all the particles completing their oscillations in the same period and being at any instant in the same phase, and the displacement of any selected one in any particular direction bearing a definite ratio to the displacement of an assigned one in an assigned direction. When a body is moving in this way it is said to be vibrating in a normal mode. For example, when a tightly stretched string of negligible flexural rigidity, such as a violin string may be taken to be, is fixed at the ends, and vibrates transversely in a normal mode, the displacements of all the particles have the same direction, and their magnitudes are proportional at any instant to the ordinates of a curve of sines. Every body possesses an infinite number of normal modes of vibration, and the frequencies (or numbers of vibrations per second) that belong to the different modes form a sequence of increasing numbers. For the string, above referred to, the fundamental tone and the various overtones form an harmonic scale, that is to say, the frequencies of the normal modes of vibration are proportional to the integers 1, 2, 3, .... In all these modes except the first the string vibrates as if it were divided into a number of equal pieces, each having fixed ends; this number is in each case the integer defining the frequency. In general the normal modes of vibration of a body are distinguished one from another by the number and situation of the surfaces (or other loci) at which some characteristic displacement or traction vanishes. The problem of determining the normal modes and frequencies of free vibration of a body of definite size, shape and constitution, is a mathematical problem of a similar character to the problem of determining the state of stress in the body when subjected to given forces. The bodies which have been most studied are strings and thin bars, membranes, thin plates and shells, including bells, spheres and cylinders. Most of the results are of special importance in their bearing upon the theory of sound.
86. The most complete success has attended the efforts of mathematicians to solve the problem of free vibrations for an isotropic sphere. It appears that the modes of vibration fall into two classes: one characterized by the absence of a radial component of displacement, and the other by the absence of a radial component of rotation (§ 14). In each class there is a doubly infinite number of modes. The displacement in any mode is determined in terms of a single spherical harmonic function, so that there are modes of each class corresponding to spherical harmonics of every integral degree; and for each degree there is an infinite number of modes, differing from one another in the number and position of the concentric spherical surfaces at which some characteristic displacement vanishes. The most interesting modes are those in which the sphere becomes slightly spheroidal, being alternately prolate and oblate during the course of a vibration; for these vibrations tend to be set up in a spherical planet by tide-generating forces. In a sphere of the size of the earth, supposed to be incompressible and as rigid as steel, the period of these vibrations is 66 minutes.
87. The theory of free vibrations has an important bearing upon the question of the strength of structures subjected to sudden blows or shocks. The stress and strain developed in a body by sudden applications of force may exceed considerably those which would be produced by a gradual application of the same forces. Hence there arises the general question of dynamical resistance, or of the resistance of a body to forces applied so quickly that the inertia of the body comes sensibly into play. In regard to this question we have two chief theoretical results. The first is that the strain produced by a force suddenly applied may be as much as twice the statical strain, that is to say, as the strain which would be produced by the same force when the body is held in equilibrium under its action; the second is that the sudden reversal of the force may produce a strain three times as great as the statical strain. These results point to the importance of specially strengthening the parts of any machine (e.g. screw propeller shafts) which are subject to sudden applications or reversals of load. The theoretical limits of twice, or three times, the statical strain are not in general attained. For example, if a thin bar hanging vertically from its upper end is suddenly loaded at its lower end with a weight equal to its own weight, the greatest dynamical strain bears to the greatest statical strain the ratio 1.63 : 1; when the attached weight is four times the weight of the bar the ratio becomes 1.84 : 1. The method by which the result just mentioned is reached has recently been applied to the question of the breaking of winding ropes used in mines. It appeared that, in order to bring the results into harmony with the observed facts, the strain in the supports must be taken into account as well as the strain in the rope (J. Perry, Phil. Mag., 1906 (vi.), vol. ii.).
88. The immediate effect of a blow or shock, locally applied to a body, is the generation of a wave which travels through the body from the locality first affected. The question of the propagation of waves through an elastic solid body is historically of very great importance; for the first really successful efforts to construct a theory of elasticity (those of S. D. Poisson, A. L. Cauchy and G. Green) were prompted, at least in part, by Fresnel’s theory of the propagation of light by transverse vibrations. For many years the luminiferous medium was identified with the isotropic solid of the theory of elasticity. Poisson showed that a disturbance communicated to the body gives rise to two waves which are propagated through it with different velocities; and Sir G. G. Stokes afterwards showed that the quicker wave is a wave of irrotational dilatation, and the slower wave is a wave of rotational distortion accompanied by no change of volume. The velocities of the two waves in a solid of density ρ are √ {(λ + 2μ)/ρ} and √ (μ/ρ), λ and μ being the constants so denoted in § 26. When the surface of the body is free from traction, the waves on reaching the surface are reflected; and thus after a little time the body would, if there were no dissipative forces, be in a very complex state of motion due to multitudes of waves passing to and fro through it. This state can be expressed as a state of vibration, in which the motions belonging to the various normal modes (§ 85) are superposed, each with an appropriate amplitude and phase. The waves of dilatation and distortion do not, however, give rise to different modes of vibration, as was at one time supposed, but any mode of vibration in general involves both dilatation and rotation. There are exceptional results for solids of revolution; such solids possess normal modes of vibration which involve no dilatation. The existence of a boundary to the solid body has another effect, besides reflexion, upon the propagation of waves. Lord Rayleigh has shown that any disturbance originating at the surface gives rise to waves which travel away over the surface as well as to waves which travel through the interior; and any internal disturbance, on reaching the surface, also gives rise to such superficial waves. The velocity of the superficial waves is a little less than that of the waves of distortion: 0.9554 √ (μ/ρ) when the material is incompressible 0.9194 √ (μ/ρ) when the Poisson’s ratio belonging to the material is 14.
89. These results have an application to the propagation of earthquake shocks (see also Earthquake). An internal disturbance should, if the earth can be regarded as solid, give rise to three wave-motions: two propagated through the interior of the earth with different velocities, and a third propagated over the surface. The results of seismographic observations have independently led to the recognition of three phases of the recorded vibrations: a set of “preliminary tremors” which are received at different stations at such times as to show that they are transmitted directly through the interior of the earth with a velocity of about 10 km. per second, a second set of preliminary tremors which are received at different stations at such times as to show that they are transmitted directly through the earth with a velocity of about 5 km. per second, and a “main shock,” or set of large vibrations, which becomes sensible at different stations at such times as to show that a wave is transmitted over the surface of the earth with a velocity of about 3 km. per second. These results can be interpreted if we assume that the earth is a solid body the greater part of which is practically homogeneous, with high values for the rigidity and the resistance to compression, while the superficial portions have lower values for these quantities. The rigidity of the central portion would be about (1.4)1012 dynes per square cm., which is considerably greater than that of steel, and the resistance to compression would be about (3.8)1012 dynes per square cm. which is much greater than that of any known material. The high value of the resistance to compression is not surprising when account is taken of the great pressures, due to gravitation, which must exist in the interior of the earth. The high value of the rigidity can be regarded as a confirmation of Lord Kelvin’s estimate founded on tidal observations (§ 83).
90. Strain produced by Heat.—The mathematical theory of elasticity as at present developed takes no account of the strain which is produced in a body by unequal heating. It appears to be impossible in the present state of knowledge to form as in § 39 a system of differential equations to determine both the stress and the temperature at any point of a solid body the temperature of which is liable to variation. In the cases of isothermal and adiabatic changes, that is to say, when the body is slowly strained without variation of temperature, and also when the changes are effected so rapidly that there is no gain or loss of heat by any element, the internal energy of the body is sufficiently expressed by the strain-energy-function (§§ 27, 30). Thus states of equilibrium and of rapid vibration can be determined by the theory that has been explained above. In regard to thermal effects we can obtain some indications from general thermodynamic theory. The following passages extracted from the article “Elasticity” contributed to the 9th edition of the Encyclopaedia Britannica by Sir W. Thomson (Lord Kelvin) illustrate the nature of these indications:—“From thermodynamic theory it is concluded that cold is produced whenever a solid is strained by opposing, and heat when it is strained by yielding to, any elastic force of its own, the strength of which would diminish if the temperature were raised; but that, on the contrary, heat is produced when a solid is strained against, and cold when it is strained by yielding to, any elastic force of its own, the strength of which would increase if the temperature were raised. When the strain is a condensation or dilatation, uniform in all directions, a fluid may be included in the statement. Hence the following propositions:—
“(1) A cubical compression of any elastic fluid or solid in an ordinary condition causes an evolution of heat; but, on the contrary, a cubical compression produces cold in any substance, solid or fluid, in such an abnormal state that it would contract if heated while kept under constant pressure. Water below its temperature (3.9° Cent.) of maximum density is a familiar instance.
“(2) If a wire already twisted be suddenly twisted further, always, however, within its limits of elasticity, cold will be produced; and if it be allowed suddenly to untwist, heat will be evolved from itself (besides heat generated externally by any work allowed to be wasted, which it does in untwisting). It is assumed that the torsional rigidity of the wire is diminished by an elevation of temperature, as the writer of this article had found it to be for copper, iron, platinum and other metals.
“(3) A spiral spring suddenly drawn out will become lower in temperature, and will rise in temperature when suddenly allowed to draw in. [This result has been experimentally verified by Joule (’Thermodynamic Properties of Solids,’ Phil. Trans., 1858) and the amount of the effect found to agree with that calculated, according to the preceding thermodynamic theory, from the amount of the weakening of the spring which he found by experiment.]
“(4) A bar or rod or wire of any substance with or without a weight hung on it, or experiencing any degree of end thrust, to begin with, becomes cooled if suddenly elongated by end pull or by diminution of end thrust, and warmed if suddenly shortened by end thrust or by diminution of end pull; except abnormal cases in which with constant end pull or end thrust elevation of temperature produces shortening; in every such case pull or diminished thrust produces elevation of temperature, thrust or diminished pull lowering of temperature.
“(5) An india-rubber band suddenly drawn out (within its limits of elasticity) becomes warmer; and when allowed to contract, it becomes colder. Any one may easily verify this curious property by placing an india-rubber band in slight contact with the edges of the lips, then suddenly extending it—it becomes very perceptibly warmer: hold it for some time stretched nearly to breaking, and then suddenly allow it to shrink—it becomes quite startlingly colder, the cooling effect being sensible not merely to the lips but to the fingers holding the band. The first published statement of this curious observation is due to J. Gough (Mem. Lit. Phil. Soc. Manchester, 2nd series, vol. i. p. 288), quoted by Joule in his paper on ‘Thermodynamic Properties of Solids’ (cited above). The thermodynamic conclusion from it is that an india-rubber band, stretched by a constant weight of sufficient amount hung on it, must, when heated, pull up the weight, and, when cooled, allow the weight to descend: this Gough, independently of thermodynamic theory, had found to be actually the case. The experiment any one can make with the greatest ease by hanging a few pounds weight on a common india-rubber band, and taking a red-hot coal in a pair of tongs, or a red-hot poker, and moving it up and down close to the band. The way in which the weight rises when the red-hot body is near, and falls when it is removed, is quite startling. Joule experimented on the amount of shrinking per degree of elevation of temperature, with different weights hung on a band of vulcanized india-rubber, and found that they closely agreed with the amounts calculated by Thomson’s theory from the heating effects of pull, and cooling effects of ceasing to pull, which he had observed in the same piece of india-rubber.”
91. Initial Stress.—It has been pointed out above (§ 20) that the “unstressed” state, which serves as a zero of reckoning for strains and stresses is never actually attained, although the strain (measured from this state), which exists in a body to be subjected to experiment, may be very slight. This is the case when the “initial stress,” or the stress existing before the experiment, is small in comparison with the stress developed during the experiment, and the limit of linear elasticity (§ 32) is not exceeded. The existence of initial stress has been correlated above with the existence of body forces such as the force of gravity, but it is not necessarily dependent upon such forces. A sheet of metal rolled into a cylinder, and soldered to maintain the tubular shape, must be in a state of considerable initial stress quite apart from the action of gravity. Initial stress is utilized in many manufacturing processes, as, for example, in the construction of ordnance, referred to in § 79, in the winding of golf balls by means of india-rubber in a state of high tension (see the report of the case The Haskell Golf Ball Company v. Hutchinson & Main in The Times of March 1, 1906). In the case of a body of ordinary dimensions it is such internal stress as this which is especially meant by the phrase “initial stress.” Such a body, when in such a state of internal stress, is sometimes described as “self-strained.” It would be better described as “self-stressed.” The somewhat anomalous behaviour of cast iron has been supposed to be due to the existence within the metal of initial stress. As the metal cools, the outer layers cool more rapidly than the inner, and thus the state of initial stress is produced. When cast iron is tested for tensile strength, it shows at first no sensible range either of perfect elasticity or of linear elasticity; but after it has been loaded and unloaded several times its behaviour begins to be more nearly like that of wrought iron or steel. The first tests probably diminish the initial stress.
92. From a mathematical point of view the existence of initial stress in a body which is “self-stressed” arises from the fact that the equations of equilibrium of a body free from body forces or surface tractions, viz. the equations of the type
93. Initial stress due to body forces becomes most important in the case of a gravitating planet. Within the earth the stress that arises from the mutual gravitation of the parts is very great. If we assumed the earth to be an elastic solid body with moduluses of elasticity no greater than those of steel, the strain (measured from the unstressed state) which would correspond to the stress would be much too great to be calculated by the ordinary methods of the theory of elasticity (§ 75). We require therefore some other method of taking account of the initial stress. In many investigations, for example those of Lord Kelvin and Sir G. H. Darwin referred to in § 83, the difficulty is turned by assuming that the material may be treated as practically incompressible; but such investigations are to some extent incomplete, so long as the corrections due to a finite, even though high, resistance to compression remain unknown. In other investigations, such as those relating to the propagation of earthquake shocks and to gravitational instability, the possibility of compression is an essential element of the problem. By gravitational instability is meant the tendency of gravitating matter to condense into nuclei when slightly disturbed from a state of uniform diffusion; this tendency has been shown by J. H. Jeans (Phil. Trans. A. 201, 1903) to have exerted an important influence upon the course of evolution of the solar system. For the treatment of such questions Lord Rayleigh (Proc. R. Soc. London, A. 77, 1906) has advocated a method which amounts to assuming that the initial stress is hydrostatic pressure, and that the actual state of stress is to be obtained by superposing upon this initial stress a stress related to the state of strain (measured from the initial state) by the same formulae as hold for an elastic solid body free from initial stress. The development of this method is likely to lead to results of great interest.
Authorities.—In regard to the analysis requisite to prove the results set forth above, reference may be made to A. E. H. Love, Treatise on the Mathematical Theory of Elasticity (2nd ed., Cambridge, 1906), where citations of the original authorities will also be found. The following treatises may be mentioned: Navier, Résumé des leçons sur l’application de la mécanique (3rd ed., with notes by Saint-Venant, Paris, 1864); G. Lamé, Leçons sur la théorie mathématique de l’élasticité des corps solides (Paris, 1852); A. Clebsch, Theorie der Elasticität fester Körper (Leipzig, 1862; French translation with notes by Saint-Venant, Paris, 1883); F. Neumann, Vorlesungen über die Theorie der Elasticität (Leipzig, 1885); Thomson and Tait, Natural Philosophy (Cambridge, 1879, 1883); Todhunter and Pearson, History of the Elasticity and Strength of Materials (Cambridge, 1886–1893). The article “Elasticity” by Sir W. Thomson (Lord Kelvin) in 9th ed. of Encyc. Brit. (reprinted in his Mathematical and Physical Papers, iii., Cambridge, 1890) is especially valuable, not only for the exposition of the theory and its practical applications, but also for the tables of physical constants which are there given. (A. E. H. L.)
- ↑ The sign of M is shown by the arrow-heads in fig. 19, for which,
with y downwards,
EI d 2y + M = 0. dx 2 - ↑ The figure is drawn for a case where the bending moment has the same sign throughout.
- ↑ M0 is taken to have, as it obviously has, the opposite sense to that shown in fig. 19.
- ↑ The line joining the points of contact must be normal to the planes.











































































































































![{\displaystyle {\tfrac {1}{2}}[({\text{X}}_{x}^{2}+{\text{Y}}_{y}^{2}+{\text{Z}}_{z}^{2})-2\sigma ({\text{Y}}_{y}{\text{Z}}_{z}+{\text{Z}}_{z}{\text{X}}_{x}+{\text{X}}_{x}{\text{Y}}_{y})+2(1+\sigma )({\text{Y}}_{z}^{2}+{\text{Z}}_{x}^{2}+{\text{X}}_{x}^{2})]/{\text{E}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a0646153b2852d248aa31fc98f8980ba67b2011)
























