MAGIC SQUARE, a square divided into equal squares, like a chess-board, in each of which is placed one of a series of consecutive numbers from 1 up to the square of the number of cells in a side, in such a manner that the sum of the numbers in each row or column and in each diagonal is constant.
From a very early period these squares engaged the attention of mathematicians, especially such as possessed a love of the marvellous, or sought to win for themselves a superstitious regard. They were then supposed to possess magical properties, and were worn, as in India at the present day, engraven in metal or stone, as amulets or talismans. According to the old astrologers, relations subsisted between these squares and the planets. In later times such squares ranked only as mathematical curiosities; till at last their mode of construction was systematically investigated. The earliest known writer on the subject was Emanuel Moscopulus, a Greek (4th or 5th century). Bernard Frenicle de Bessy constructed magic squares such that if one or more of the encircling bands of numbers be taken away the remaining central squares are still magical. Subsequently Poignard constructed squares with numbers in arithmetical progression, having the magical summations. The later researches of Phillipe de la Hire, recorded in the Mémoires de l’Académie Royale in 1705, are interesting as giving general methods of construction. He has there collected the results of the labours of earlier pioneers; but the subject has now been fully systematized, and extended to cubes.
Two interesting magical arrangements are said to have been given by Benjamin Franklin; these have been termed the “magic square of squares” and the “magic circle of circles.” The first (fig. 1) is a square divided into 256 squares, i.e. 16 squares along a side, in which are placed the numbers from 1 to 256. The chief properties of this square are (1) the sum of the 16 numbers in any row or column is 2056; (2) the sum of the 8 numbers in half of any row or column is 1028, i.e. one half of 2056; (3) the sum of the numbers in two half-diagonals equals 2056; (4) the sum of the four corner numbers of the great square and the four central numbers equals 1028; (5) the sum of the numbers in any 16 cells of the large square which themselves are disposed in a square is 2056. This square has other curious properties. The “magic circle of circles” (fig. 2) consists of eight annular rings and a central circle, each ring being divided into eight cells by radii drawn from the centre; there are therefore 65 cells. The number 12 is placed in the centre, and the consecutive numbers 13 to 75 are placed in the other cells. The properties of this figure include the following: (1) the sum of the eight numbers in any ring together with the central number 12 is 360, the number of degrees in a circle; (2) the sum of the eight numbers in any set of radial cells together with the central number is 360; (3) the sum of the numbers in any four adjoining cells, either annular, radial, or both radial and two annular, together with half the central number, is 180.
Construction of Magic Squares.—A square of 5 (fig. 3) has
adjoining it one of the eight equal squares by which any square
may be conceived to
be surrounded, each of
which has two sides
resting on adjoining
squares, while four have sides resting on
the surrounded square,
and four meet it only
at its four angles. 1, 2,
3 are placed along the path of a knight in chess; 4, along the same
path, would fall in a cell of the outer square, and is placed instead
in the corresponding cell of the original square; 5 then falls
within the square. a, b, c, d are placed diagonally in the square;
but e enters the outer square, and is removed thence to the same
cell of the square it had left. α, β, γ, δ, ε pursue another regular
course; and the diagram shows how that course is recorded in
the square they have twice left. Whichever of the eight surrounding
squares may be entered, the corresponding cell of the
central square is taken instead. The 1, 2, 3, . . ., a, b, c, . . .,
α, β, γ, . . . are said to lie in “paths.”
have sides resting on
the surrounded square,
and four meet it only
at its four angles. 1, 2,
3 are placed along the path of a knight in chess; 4, along the same
path, would fall in a cell of the outer square, and is placed instead
in the corresponding cell of the original square; 5 then falls
within the square. a, b, c, d are placed diagonally in the square;
but e enters the outer square, and is removed thence to the same
cell of the square it had left. α, β, γ, δ, ε pursue another regular
course; and the diagram shows how that course is recorded in
the square they have twice left. Whichever of the eight surrounding
squares may be entered, the corresponding cell of the
central square is taken instead. The 1, 2, 3, . . ., a, b, c, . . .,
α, β, γ, . . . are said to lie in “paths.”
 | ||
| Fig. 4. | Fig. 5. | Fig. 6. |
 | ||
| Fig. 7. | Fig. 8. | Fig. 9. |
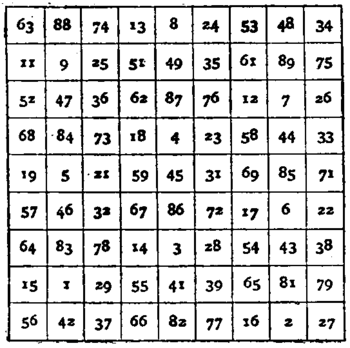
Squares whose Roots are Odd.—Figs 4, 5, and 6 exhibit one of the earliest methods of constructing magic squares. Here the 3’s in fig. 4 and 2’s in fig. 5 are placed in opposite diagonals to secure the two diagonal summations; then each number in fig. 5 is multiplied by 5 and added to that in the corresponding square in fig. 4, which gives the square of fig. 6. Figs. 7, 8 and 9 give De la Hire’s method; the squares of figs. 7 and 8, being combined, give the magic square of fig. 9. C. G. Bachet arranged the numbers as in fig. 10, where there are three numbers in each of four surrounding squares; these being placed in the corresponding cells of the central square, the square of fig. 11 is formed. He also constructed squares such that if one or more outer bands of numbers are removed the remaining central squares are magical. His method of forming them may be understood from a square of 5. Here each summation is 5×13; if therefore 13 is subtracted from each number, the summations will be zero, and the twenty-five cells will contain the series ± 1, ± 2, ± 3, . . . ± 12, the odd cell having 0. The central square of 3 is formed with four of the twelve numbers with + and − signs and zero in the middle; the band is filled up with the rest, as in fig. 12; then, 13 being added in each cell, the magic square of fig. 13 is obtained.
 | |
| Fig. 10. | Fig. 11. |
 | |
| Fig. 12. | Fig. 13. |
 | ||
| Fig. 14. | Fig. 15. | Fig. 16. |
 | ||
| Fig. 17. | Fig. 18. | Fig. 19. |
 |
| Fig. 20. |
Squares whose Roots are Even.—These were constructed in various ways, similar to that of 4 in figs. 14, 15 and 16. The numbers in fig. 15 being multiplied by 4, and the squares of figs. 14 and 15 being superimposed, give fig. 16. The application of this method to squares the half of whose roots are odd requires a complicated adjustment. Squares whose half root is a multiple of 4, and in which there are summations along all the diagonal paths, may be formed, by observing, as when the root is 4, that the series 1 to 16 may be changed into the series 15, 13, . . . 3, 1, −1, −3, . . . −13, −15, by multiplying each number by 2 and subtracting 17; and, vice versa, by adding 17 to each of the latter, and dividing by 2. The diagonal summations of a square, filled as in fig. 17, make zero; and, to obtain the same in the rows and columns, we must assign such values to the p’s and q’s as satisfy the equations p1 + p2 + a1 + a2 = 0, p3 + p4 + a3 + a4 = 0, p1 + p3 − a1 − a3 = 0, and p2 + p4 − a2 − a4 = 0,—a solution of which is readily obtained by inspection, as in fig. 18; this leads to the square, fig. 19. When the root is 8, the upper four subsidiary rows may at once be written, as in fig. 20; then, if 65 be added to each, and the sums halved, the square is completed. In such squares as these, the two opposite squares about the same diagonal (except that of 4) may be turned through any number of right angles, in the same direction, without altering the summations.
Nasik Squares.—Squares that have many more summations than in rows, columns and diagonals were investigated by A. H. Frost (Cambridge Math. Jour., 1857), and called Nasik squares, from the town in India where he resided; and he extended the method to cubes, various sections of which have the same singular properties. In order to understand their construction it will be necessary to
consider carefully fig. 21, which shows that, when the root is a prime,
and not composite, number, as 7, eight letters a, b, . . . h may proceed
from any, the same, cell, suppose that marked 0, each letter being
repeated in the cells along different paths. These eight paths are
called “normal paths,” their number being one more than the root.
Observe here that, excepting the cells from which any two letters
start, they do not occupy again the
Fig. 21
same cell, and that two letters, starting
from any two different cells along different
paths, will appear together in one
and only one cell. Hence, if p1 be placed
in the cells of one of the n + 1 normal
paths, each of the remaining n normal
paths will contain one, and only one,
of these p1’s. If now we fill each row
with p2, p3, . . . pn in the same order,
commencing from the p1 in that row,
the p2’s, p3’s and pn’s will lie each in a
path similar to that of p1, and each of
the n normal paths will contain one,
and only one, of the letters p1, p2,. . . pn,
whose sum will be Σp. Similarly, if
q1 be placed along any of the normal paths, different from that of
the p’s, and each row filled as above with the letters q2, q3, . . . qn,
the sum of the q’s along any normal path different from that of
the q1 will be Σq. The n2 cells of the square will now be found to
contain all the combinations of the p’s and q’s; and if the q’s
be multiplied by n, the p’s made equal to 1, 2, . . . n, and the q’s
to 0, 1, 2, . . . (n − 1) in any order, the Nasik square of n will be
obtained, and the summations along all the normal paths, except
those traversed by the p’s and q’s, will be the constant Σnq + Σp.
When the root is an odd composite number, as 9, 15, &c., it will be
found that in some paths, different from the two along which the
p1 and q1 were placed, instead of having each of the p’s and q’s,
some will be wanting, while some are repeated. Thus, in the case
of 9, the triplets, p1p4p7, p2p5p8, p3p6p9, and q1q4q7, q2q5q8, q3q6q9 occur,
each triplet thrice, along paths whose summation should be—Σp 45
and Σr 36. But if we make p1, p2, . . . p9, = 1, 3, 6, 5, 4, 7, 9, 8, 2, and
the r1, r2, . . . r9 = 0, 2, 5, 4, 3, 6, 8, 7, 1, thrice each of the above sets
of triplets will equal Σp and
Σq respectively. If now the
q’s are multiplied by 9, and
added to the p’s in their
several cells, we shall have a
Nasik square, with a constant
summation along eight of its
ten normal paths. In fig. 22
the numbers are in the nonary
scale; that in the centre is
the middle one of 1 to 92, and
the sum of pair of numbers
equidistant from and opposite
to the central 45 is twice 45;
and the sum of any number
and the 8 numbers 3 from it,
diagonally, and in its row and
column, is the constant Nasical
summation, e.g. 72 and
32, 22, 76, 77, 26, 37, 36, 27. The numbers in fig. 22 being kept
in the nonary scale, it is not necessary to add any nine of them
together in order to test the Nasical summation; for, taking the
first column, the figures in the place of units are seen at once
to form the series, 1, 2, 3, . . . 9, and those in the other place three
triplets of 6, 1, 5. For the squares of 15 the p’s and q’s may be
respectively 1, 2, 10, 8, 6, 14, 15, 11, 4, 13, 9, 7, 3, 12, 5, and 0, 1, 9, 7,
5, 13, 14, 10, 3, 12, 8, 6, 2, 11, 4, where five times the sum of every
third number and three times the sum of every fifth number makes
Σp and Σq; then, if the q’s are multiplied by 15, and added to the
p’s, the Nasik square of 15
is obtained. When the root
is the multiple of 4, the same
process gives us, for the
square of 4, fig. 23. Here
the columns give Σp, but
alternately 2q1, 2q3, and 2q2,
2q4; and the rows give Σq,
but alternately 2p1, 2p3,
and 2p2, 2p4; the diagonals
giving Σp and Σq. If p1, p2, p3, p4 and q1, q2, q3, q4 be 1, 2, 4, 3,
and 0, 1, 3, 2, we have the Nasik square of fig. 24. A square like this
is engraved in the Sanskrit character on the gate of the fort of
Gwalior, in India. The squares of higher multiples of 4 are readily
obtained by a similar adjustment.
 |
| Fig. 22. |
 |  |
| Fig. 23. | Fig. 24. |
Nasik Cubes.—A Nasik cube is composed of n3 small equal cubes,
here called cubelets, in the centres of which the natural numbers
from 1 to n3 are so placed that every section of the cube by planes
Fig. 25—Nasik Cube.
perpendicular to an edge has the properties of a Nasik square; also
sections by planes perpendicular to a face, and passing through the
cubelet centres of any path of Nasical summation in that face.
Fig. 25 shows by dots the way in which these cubes are constructed.
A dot is here placed on three faces of a cubelet at the corner, showing
that this cubelet belongs to each of the faces AOB, BOC, COA, of
the cube. Dots are placed on the cubelets of some path of AOB
(here the knight’s path), beginning from O, also on the cubelets of
a knight’s path in BOC. Dots are now placed in the cubelets of
similar paths to that on BOC in the other six sections parallel to
BOC, starting from their dots in AOB. Forty-nine of the three
hundred and forty-three cubelets will now contain a dot; and
it will be observed that the dots in sections perpendicular to BO
have arranged themselves in similar
paths. In this manner, p1, q1, r1
being placed in the corner cubelet
O, these letters are severally placed
in the cubelets of three different
paths of AOB, and again along
any similar paths in the seven
sections perpendicular to AO, starting
from the letters’ position in
AOB. Next, p2q2r2, p3q3r3, . . .
p7q7r7 are placed in the other cubelets
of the edge AO, and dispersed
in the same manner as p1q1r1.
Every cubelet will then be found to
contain a different combination of
the p’s, q’s and r’s. If therefore
the p’s are made equal to 1, 2,
. . . 7, and the q’s and r’s to 0,
1, 2, . . . 6, in any order, and the
q’s multiplied by 7, and the r’s
by 72, then, as in the case of the squares, the 73 cubelets will
contain the numbers from 1 to 73, and the Nasical summations will
be Σ72r + Σ7q + p. If 2, 4, 5 be values of r, p, q, the number for
that cubelet is written 245 in the septenary scale, and if all the
cubelet numbers are kept thus, the paths along which summations
are found can be seen without adding, as the seven numbers
would contain 1, 2, 3, . . . 7 in the unit place, and 0, 1, 2, . . . 6 in
each of the other places. In all Nasik cubes, if such values are given
to the letters on the central cubelet that the number is the middle
one of the series 1 to n3, the sum of all the pairs of numbers opposite
to and equidistant from the middle number is the double of it.
Also, if around a Nasik cube the twenty-six surrounding equal cubes
be placed with their cells filled with the same numbers, and their
corresponding faces looking the same way,—and if the surrounding
space be conceived thus filled with similar cubes, and a straight line
of unlimited length be drawn through any two cubelet centres, one
in each of any two cubes,—the numbers along that line will be found
to recur in groups of seven, which (except in the three cases where
the same p, q or r recur in the group) together make the Nasical
summation of the cube. Further, if we take n similarly filled
Nasik cubes of n, n new letters, s1, s2, . . . sn, can be so placed, one in
each of the n4 cubelets of this group of n cubes, that each shall
contain a different combination of the p’s, q’s, r’s and s’s.
 |
| Fig. 26. |
 | |
| Fig. 27. | Fig. 28. |
This is done by placing s1 on each of the n2 cubelets of the first cube that contain p1, and on the n2 cubelets of the 2d, 3d, . . . and nth cube that contain p2, p3, . . . pn respectively. This process is repeated with s2, beginning with the cube at which we ended, and so on with the other s’s; the n4 cubelets, after multiplying the q’s, r’s, and s’s by n, n2, and n3 respectively, will now be filled with the numbers from 1 to n4, and the constant summation will be Σn3s + Σn2r + Σnq + Σp. This process may be carried on without limit; for, if the n cubes are placed in a row with their faces resting on each other, and the corresponding faces looking the same way, n such parallelepipeds might be put side by side, and the n5 cubelets of this solid square be Nasically filled by the introduction of a new letter t; while, by introducing another letter, the n6 cubelets of the compound cube of n3 Nasik cubes might be filled by the numbers from 1 to n6, and so ad infinitum. When the root is an odd composite number the values of the three groups of letters have to be adjusted as in squares, also in cubes of an even root. A similar process enables us to place successive numbers in the cells of several equal squares in which the Nasical summations are the same in each, as in fig. 26.
Among the many ingenious squares given by various writers, this article may justly close with two by L. Euler, in the Histoire de l’académie royale des sciences (Berlin, 1759). In fig. 27 the natural numbers show the path of a knight that moves within an odd square in such a manner that the sum of pairs of numbers opposite to and equidistant from the middle figure is its double. In fig. 28 the knight returns to its starting cell in a square of 6, and the difference between the pairs of numbers opposite to and equidistant from the middle point is 18.
A model consisting of seven Nasik cubes, constructed by A. H. Frost, is in the South Kensington Museum. The centres of the cubes are placed at equal distances in a straight line, the similar faces looking the same way in a plane parallel to that line. Each of the cubes has seven parallel glass plates, to which, on one side, the seven numbers in the septenary scale are fixed, and behind each, on the other side, its value in the common scale. 1201, the middle number from 1 to 74 occupies the central cubelet of the middle cube. Besides each cube having separately the same Nasical summation, this is also obtained by adding the numbers in any seven similarly situated cubelets, one in each cube. Also, the sum of all pairs of numbers, in a straight line, through the central cube of the system, equidistant from it, in whatever cubes they are, is twice 1201. (A. H. F.)
Fennell’s Magic Ring.—It has been noticed that the numbers of magic squares, of which the extension by repeating the rows and columns of n numbers so as to form a square of 2n − 1 sides yields n2 magic squares of n sides, are arranged as if they were all inscribed round a cylinder and also all inscribed on another cylinder at right angles to the first. C. A. M. Fennell explains this apparent anomaly by describing such magic squares as Mercator’s projections, so to say, of “magic rings.”
The surface of these magic rings is symmetrically divided into n2 quadrangular compartments or cells by n equidistant zonal circles parallel to the circular axis of the ring and by n transverse circles which divide each of the n zones between any two neighbouring zonal circles into n equal quadrangular cells, while the zonal circles divide the sections between two neighbouring transverse circles into n unequal quadrangular cells. The diagonals of cells which follow each other passing once only through each zone and section, form similar and equal closed curves passing once quite round the circular axis of the ring and once quite round the centre of the ring. The position of each number is regarded as the intersection of two diagonals of its cell. The numbers are most easily seen if the smallest circle on the surface of the ring, which circle is concentric with the axis, be one of the zonal circles. In a perfect magic ring the sum of the numbers of the cells whose diagonals form any one of the 2n diagonal curves aforesaid is 12n (n2 + 1) with or without increment, i.e. is the same sum as that of the numbers in each zone and each transverse section. But if n be 3 or a multiple of 3, only from 2 to n of the diagonal curves carry the sum in question, so that the magic rings are imperfect; and any set of numbers which can be arranged to make a perfect magic ring or magic square can also make an imperfect magic ring, e.g. the set 1 to 16 if the numbers 1, 6, 11, 16 lie thus on a diagonal curve instead of in the order 1, 6, 16, 11. From a perfect magic ring of n2 cells containing one number each, n2 distinct magic squares can be read off; as the four numbers round each intersection of a zonal circle and a transverse circle constitute corner numbers of a magic square. The shape of a magic ring gives it the function of an indefinite extension in all directions of each of the aforesaid n2 magic squares. (C. A. M. F.)
See F. E. A. Lucas, Récréations mathématiques (1891–1894); W. W. R. Ball, Mathematical Recreations (1892); W. E. M. G. Ahrens, Mathematische Unterhaltungen und Spiele (1901); H. C. H. Schubert, Mathematische Mussestunden (1900). A very detailed work is B. Violle, Traité complet des carrés magiques (3 vols., 1837–1838). The theory of “path nasiks” is dealt with in a pamphlet by C. Planck (1906).

