PARABOLA, a plane curve of the second degree. It may be defined as a section of a right circular cone by a plane parallel to a tangent plane to the cone, or as the locus of a point which moves so that its distances from a fixed point and a fixed line are equal. It is therefore a conic section having its eccentricity equal to unity. The parabola is the curve described by a projectile which moves in a non-resisting medium under the influence of gravity (see Mechanics). The general relations between the parabola, ellipse and hyperbola are treated in the articles Geometry, Analytical, and Conic Sections; and various projective properties are demonstrated in the article Geometry, Projective. Here only the specific properties of the parabola will be given.
The form of the curve is shown in fig. 1, where P is a point on the curve equidistant from the fixed line AB, known as the directrix, and the fixed point F known as 
Fig. 1. the focus. The line CD passing through the focus and perpendicular to the directrix is the axis or principal diameter, and meets the curve in the vertex G. The line FL perpendicular to the axis, and passing through the focus, is the semilatus rectum, the latus rectum being the focal chord parallel to the directrix. Any line parallel to the axis is a diameter, and the parameter of any diameter is measured by the focal chord drawn parallel to the tangent at the vertex of the diameter and is equal to four times the focal distance of the vertex. To construct the parabola when the focus and directrix are given, draw the axis CD and bisect CF at G, which gives the vertex. Any number of points on the parabola are obtained by taking any point E on the directrix, joining EG and EF and drawing FP so that the angles PFE and DFE are equal. Then EG produced meets FP in a point on the curve. By joining the points so obtained the parabola may be described. A mechanical construction, when the same conditions are given, consists in taking a rigid bar ABC bent at right angles at B (fig. 2), 
Fig. 2. and fastening a string of length BC to C and F. Then if a pencil be placed along BC so as to keep the string taut, and the limb AB be slid along the directrix, the pencil will trace out the parabola.
Properties which may be readily deduced by euclidian methods from the definition include the following: the tangent at any point bisects the angle between the focal distance and the perpendicular on the directrix and is equally inclined to the focal distance and the axis; tangents at the extremities of a focal chord intersect at right angles on the directrix, and as a corollary we have that the locus of the intersection of tangents at right angles is the directrix; the circumcircle of a triangle circumscribing a parabola passes through the focus; the sub-tangent is equal to twice the abscissa of the point of contact; the subnormal is constant and equals the semilatus rectum; and the radius of curvature at a point P is 2 (FP)32/a12 where a is the semilatus rectum and FP the focal distance of P.
A fundamental property of the curve is that the line at infinity is a tangent (see Geometry, Projective), and it follows that the centre and the second real focus and directrix are at infinity. It also follows that a line half-way between a point and its polar and parallel to the latter touches the parabola, and therefore the lines joining the middle points of the sides of a self-conjugate triangle form a circumscribing triangle, and also that the nine-point circle of a self-conjugate triangle passes through the focus. The orthocentre of a triangle circumscribing a parabola is on the directrix; a deduction from this theorem is that the centre of the circumcircle of a self-conjugate triangle is on the directrix (“Steiner’s Theorem”).
In the article Geometry, Analytical, it is shown that the general equation of the second degree represents a parabola when the highest terms form a perfect square. This is the analytical expression of the projective property that the line at infinity is a tangent. The simplest equation to the parabola is that which is referred to itsAnalytic Geometry. axis and the tangent at the vertex as the axes of co-ordinates, when it assumes the form where 2a=semilatus rectum; this may be deduced directly from the definition. An equation of similar form is obtained when the axes of co-ordinates are any diameter and the tangent at the vertex. The equations to the tangent and normal at the point are and , and may be obtained by general methods (see Geometry, Analytical, and Infinitesimal Calculus). More convenient forms in terms of a single parameter are deduced by substituting , (for on eliminating m between these relations the equation to the parabola is obtained). The tangent then becomes and the normal . The envelope of this last equation is , which shows that the evolute of a parabola is a semi-cubical parabola (see below Higher Orders). The cartesian equation to a parabola which touches the coordinate axes is , and the polar equation when the focus is the pole and the axis the initial line is .
The equation to a parabola in triangular co-ordinates is generally derived by expressing the condition that the line at infinity is a tangent in the equation to the general conic. For example, in trilinear co-ordinates, the equation to the general conic circumscribing the triangle of reference is ; for this to be a parabola the line must be a tangent. Expressing this condition we obtain as the relation which must hold between the co-efficients of the above equation and the sides of the triangle of reference for the equation to represent a parabola. Similarly, the conditions for the inscribed conic to be a parabola is , and the conic for which the triangle of reference is self-conjugate is . The various forms in areal co-ordinates may be derived from the above by substituting for l, for m and for n, or directly by expressing the condition for tangency of the line to the conic expressed in areal co-ordinates. In tangential (p, q, r) co-ordinates the inscribed and circumscribed conics take the forms and ; these are parabolas when and respectively.
The length of a parabolic arc can be obtained by the methods of the infinitesimal calculus; the curve is directly quadrable, the area of any portion between two ordinates being two thirds of the circumscribing parallelogram. The pedal equation with the focus as origin is ; the first positive pedal for the vertex is the cissoid (q.v.) and for the focus the directrix. (See Infinitesimal Calculus.)
References.—Geometrical constructions of the parabola are to be found in T. H. Eagles’ Plane Curves (1885). See the bibliography to the articles Conic Sections; Geometry, Analytical; and Geometry, Projective.
In the geometry of plane curves, the term parabola is often used to denote the curves given by the general equation , thus is the quadratic or Apollonian parabola; is the cubic parabola, is the biquadratic parabola; semi parabolas have the general equation , thus is the semicubicalHigher Orders. parabola and the semibiquadratic parabola. These curves were investigated by René Descartes, Sir Isaac Newton, Colin Maclaurin and others. Here we shall treat only the more important forms.
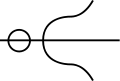
The cartesian parabola is a cubic curve which is also known as the trident of Newton on account of its three-pronged form. Its equation is , and it consists of two legs asymptotic to the axis of y and two parabolic legs (fig. 3). The simplest form is , in this case the serpentine position shown in the figure degenerates into a point of inflexion. Descartes used the curve to solve sextic equations by determining its intersections with a circle; mechanical constructions were given by Descartes (Geometry, lib. 3) and Maclaurin (Organica geometrica).
The cubic parabola (fig. 4) is a cubic curve having the equation . It consists of two parabolic branches tending in opposite directions. John Wallis utilized the intersections of this curve with a right line to solve cubic equations, and Edmund Halley solved sextic equations with the aid of a circle.
Diverging parabolas are cubic curves given by the equation . Newton discussed the five forms which arise from the relations of the roots of the cubic equation.
 |
 |
 | ||
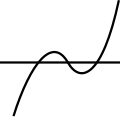
| Fig. 3. | Fig. 4. | Fig. 5. |
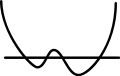
When all the roots are real and unequal the curve consists of a closed oval and a parabolic branch (fig. 5). As the two lesser roots are made more and more equal the oval shrinks in size and ultimately becomes a real conjugate point, and the curve, the equation of which is (in which a > b) consists of this point and a bell-like branch resembling the right-hand member of fig. 5. If two roots are imaginary the equation is and the curve resembles the parabolic branch, as in the preceding case. This is sometimes termed the campaniform (or bell-shaped) parabola. If the two greater roots are equal the equation is (in which a < b) and the curve assumes the form shown in fig. 6, and is known as the nodated parabola. Finally, if all the roots are equal, the equation becomes this curve is the cuspidal or semi-cubical parabola (fig. 7). This curve, which is sometimes termed the Neilian parabola after William Neil (1637–1670), is the evolute of the ordinary parabola, and is especially interesting as being the first curve to be rectified. This was accomplished in 1657 by Neil in England, and in 1659 by Heinrich van Haureat in Holland. Newton showed that all the five varieties of the diverging parabolas may be exhibited as plane sections of the solid of revolution of the semi-cubical parabola. A plane oblique to the axis and passing below the vertex gives the first variety; if it passes through the vertex, the second form; if above the vertex and oblique or parallel to the axis, the third form; if below the vertex and touching the surface, the fourth form, and if the plane contains the axis, the fifth form results (see Curve).
 |
 |
| Fig. 6. | Fig. 7. |
 |
 |
 | ||
| Fig. 8. | Fig. 9. | Fig. 10. |
The biquadratic parabola has, in its most general form, the equation , and consists of a serpentinous and two parabolic branches (fig. 8).If all the roots of the quartic in x are equal the curve assumes the form shown in fig. 9, the axis of x being a double tangent. If the two middle roots are equal, fig. 10 results. Other forms which correspond to other relations between the roots can be readily deduced from the most general form. (See Curve; and Geometry, Analytical.)










































