1911 Encyclopædia Britannica/Railways/Locomotive Power
Locomotive Power
The term “power” is used in technical sense to mean the rate at which work is done against a resistance, and is measured in units of energy expended per unit of time. The unit of power commonly used by engineers is the horse-power, and this unit corresponds to a rate of working of 550 foot-℔ of work per second. The problems arising out of the special consideration of the power required to propel a railway train against the resistances opposing its motion, the way the power is applied to trains, the agent by means of which the power is exerted, are conveniently grouped together under the general heading of Locomotive Power. There are certain fundamental relations common to all tractive problems, and these are briefly considered in §§ 1 and 2, after which the article refers particularly to steam locomotives, although §§ 4, 5, 7, 8, 9, and 10 have a general application to all modes of traction.
§ 1. Fundamental Relations.—The resistance against which a train is moved along a railway is overcome by means of energy obtained from the combustion of fuel, or in some few cases by energy obtained from a waterfall. If the total resistance against which the train is maintained in motion with an instantaneous velocity of V feet per second is R, the rate at which energy is expended in moving the train is represented by the product RV, and this must be the rate at which energy is supplied to the train after deducting all losses due to transmission from the source of power. Thus if R is equal to 10,000 ℔ when the velocity is 44 ft. per second, equivalent to 30 m. per hour, the rate of working against the resistance is 440,000 foot-℔ per second.
In whatever form energy is produced and distributed to the train it ultimately appears as mechanical energy applied to turn on e or more axles against the resistance to their rotation imposed by the weight on the wheels and the motion of the train.
The rate at which work is done on a particular axle is measured by the product Tω, where T is the torque or turning moment exerted on the axle by the motor or mechanism applied to it for this purpose, and ω is the angular velocity of the axle in radians per second. Hence if all the energy supplied to the train is utilized at one axle there is the fundamental relation
| (1) |
Continuing the above arithmetical illustration, if the wheels to the axle of which the torque is applied are 4 ft. diameter, ω=44/2=22 radians per second, and therefore T=440,000/22=20,000 ℔ ft. If the energy supplied is distributed between several axles the relation becomes
| (2) |
where T₁, T₂, T₃, &c. are the torques on the axles whose respective angular velocities are ω₁, ω₂, ω₃, &c.
The fundamental condition governing the design of all tractive machinery is that the wheels belonging to the axles to which torque is applied shall roll along the rails without slipping, and exert a tractive force on the train.

|
| Fig. 16.—Wheel and Connexion to Frame. |
The fundamental relation between the applied torque and the tractive force F will be understood from fig. 16, which shows in a diagrammatic form a wheel and axle connected to the framework of a vehicle, in the way adopted for railway trains. The journal of the axle A, is carried in a bearing or axle-box B, which is free to move vertically in the wide vertical slot G, formed in the frame and called generally “the horns,” under the control of the spring. The weight W₁ carried by the part of the frame supported by the wheel (whose diameter is D) is transmitted first to the pins P₁, P₂ which are fixed to the frame, and then to the spring links. L₁, L₂, which are jointed at their respective ends to the spring S, the centre of which rests on the axle-box.
Let a couple be applied to the axle tending to turn it in the direction shown by the arrow. This couple, we may assume, will be equally divided between the two wheels, so that the torque acting on each will be 12T. Assuming the wheels to roll along the rail without slipping, this couple will be equivalent to the couple formed by the equal opposite and parallel forces, F₁ acting in the direction shown, from the axle-box on to the frame, and F₁=μθ, acting along the rail. The torque corresponding to this couple is F₁ × 12D=12μW₁D, and hence follows the fundamental relation, 12T=12F₁D=12μW₁D, or if W now represents the weight supported by the axle, F will be the tractive force exerted on the frame by the two axle-boxes to propel the vehicle, and the more convenient relation is established,
| (3) |
If T has a greater value than this relation justifies the wheels will slip. F is called the “tractive force” at the rail. The coefficient of friction μ is a variable quantity depending upon the state of the rails, but is usually taken to be 15. This is the fundamental equation between the forces acting, however the torque may be applied. Multiplying through by ω we obtain
| (4) |
This is a fundamental energy equation for any form of locomotive in which there is only one driving-axle.
The couple T is necessarily accompanied by an equal and opposite couple acting on the frame, which couple endeavours to turn the frame in the opposite direction to that in which the axle rotates. The practical effect of this opposite couple is slightly to tilt the frame and thus to redistribute slightly the weights on the wheels carrying the vehicle.
If there are several driving-axles in a train, the product Tω must be estimated for each separately; then the sum of the products will be equal to RV. In equation (4) there is a fixed relation between ω, V and D given by the expression
| ω=2V/D | (5) |
Here D is in feet, V in feet per second and ω in radians per second. If the speed is given in miles per hour, S say,
| V=1·466 S | (6) |
The revolutions of the axle per second, n, are connected with the radians turned through per second by the relation
| n=ω/2π=ω/6·38 | (7) |
§ 2. Methods of Applying Locomotive Power.—By locomotive power is to be understood the provision of power to maintain the rates of working on the driving-axles of a train indicated by the relation (4). The most usual way of providing this power is by the combustion of coal in the fire-box of a boiler and the utilization of the steam produced in a steam-engine, both boiler and engine being carried on a frame mounted on wheels in such a way that the crankshaft of the steam-engine becomes the driving-axle of the train. From equation (3) it is clear that the wheels of the driving-axle must be heavily loaded in order that F may have a value sufficiently great to propel the train. The maximum weight which one pair of wheels are usually allowed to carry on a first-class track is from 18 to 20 tons. If a larger value of the tractive force is required than this provides for, namely from 4 to 5 tons, the driving-wheels are coupled to one or more pairs of heavily loaded wheels, forming a class of what are called “coupled engines” in contradistinction to the “single engine” with a single pair of loaded driving-wheels. Mechanical energy may be developed in bulk at a central station conveniently situated with regard to a coal-field or a waterfall, and after transformation by means of electric generators into electric energy it may be transmitted to the locomotive and then by means of electric motors be retransformed into mechanical energy at the axles to which the motors are applied. Every axle of an electric locomotive may thus be subjected to a torque, and the large weight which must be put on one pair of wheels in order to secure sufficient adhesion when all the driving is done from one axle may be distributed through as many pairs of wheels as desired. In fact, there need be no specially differentiated locomotive at all. Motors may be applied to every axle in the train, and their individual torques adjusted to values suitable to the weights naturally carried by the several axles. Such an arrangement would be ideally perfect from the point of view of the permanent-way engineer, because it would then be possible to distribute the whole of the load uniformly between the wheels. This perfection of distribution is practically attained in present-day practice by the multiple control system of operating an electric train, where motors are applied to a selected number of axles in the train, all of them being under the perfect control of the driver.
The fundamental difference between the two methods is that while the mechanical energy developed by a steam engine is in the first case applied directly to the driving-axle of the locomotive, in the second case it is transformed into electrical energy, transmitted over relatively long distances, and retransformed into mechanical energy on the driving-axles of the train. In the first case all the driving is done on one or at most two axles; sufficient tractive force being obtained by coupling these axles when necessary to others carrying heavy loads. In the second case every axle in the train may be made a driving-axle if desired, in which case the locomotive as a separate machine disappears. In the second case, however, there are all the losses due to transmission from the central station to the train to be considered, as well as the cost of the transmitting apparatus itself. Ultimately the question resolves itself into one of commercial practicability. For suburban traffic with a service at a few minutes interval and short distances between the stations electric traction has proved itself to be superior in many respects to the steam locomotive, but for main line traffic and long distance runs it has not yet been demonstrated that it is commercially feasible, though it is known to be practically possible. For the methods of electric traction see Traction; the remainder of the present article will be devoted to the steam locomotive.
§ 3. General Efficiency of Steam Locomotive.—One pound of good Welsh coal properly burned in the fire-box of a locomotive yields about 15,000 British thermal units of heat at a temperature high enough to enable from 50 to 80% to flow across the boiler-heating surface to the water, the rest escaping up the chimney with the furnace gases. The steam produced in consequence of this heat transference from the furnace gas to the water carries heat to the cylinder, where 7 to 11% is transformed into mechanical energy, the remainder passing away up the chimney with the exhaust steam. The average value of the product of these percentages, namely 0·65 × 0·09 = 0·06 say, may be used to investigate generally the working of a locomotive; the actual value could only be determined by experiment in any particular case. With this assumption, 0·06 is the fraction of the heat energy of the coal which is utilized in the engine cylinders as mechanical work; that is to say, of the 15,000 B.Th.U. produced by the combustion of 1 ℔ of coal, 15,000 × 0·06 = 900 only are available for tractive purposes.
Coals vary much in calorific value, some producing only 12,000 B.Th.U. per ℔ when burnt, whilst 15,500 is obtained from the best Welsh coals. Let E represent the pounds of coal burnt per hour in the fire-box of a locomotive, and let c be the calorific value in B.Th.U. per ℔; then the mechanical energy available in foot pounds per hour is approximately 0·06 × 778 × Ec, and this expressed in horse-power units gives
A “perfect engine” receiving and rejecting steam at the same temperatures as the actual engine of the locomotive, would develop about twice this power, say 1400 I.H.P. This figure represents the ideal but unattainable standard of performance. This question of the standard engine of comparison, and the engine efficiency is considered in § 15 below, and the boiler efficiency in § 11 below.
The indicated horse-power developed by a cylinder may always be ascertained from an indicator diagram and observations of the speed. Let p be the mean pressure in pounds per square inch, calculated from an indicator diagram taken from a particular cylinder when the speed of the crank-shaft is n revolutions per second. Also let l be the length of the stroke in feet and let a be the area of one cylinder in square inches, then, assuming two cylinders of equal size,
| (8) |
The I.H.P. at any instant is equal to the total rate at which energy is required to overcome the tractive resistance R. The horsepower available at the driving-axle, conveniently called the brake horse-power, is from 20 to 30 % less than the indicated horse-power, and the ratio, B.H.P./I.H.P. = e, is called the mechanical efficiency of the steam engine. The relation between the b.h.p. and the torque on the driving-axle is
| (9) |
It is usual with steam locomotives to regard the resistance R as including the frictional resistances between the cylinders and the driving-axle, so that the rate at which energy is expended in moving the train is expressed either by the product RV, or by the value of the indicated horse-power, the relation between them being
| (10) |
or in terms of the torque
| (11) |
The individual factors of the product RV may have any value consistent with equation (10) and with certain practical conditions, so that for a given value of the I.H.P. R must decrease if V increases. Thus if the maximum horse-power which a locomotive can develop is 1000, the tractive resistance R, at 60 m. per hour ( = 88 ft. per second) is R = (1000 × 550)/88 =6250 ℔. If, however, the speed is reduced to 15 m. per hour ( =22 ft. per second) R increases to 25,000 ℔. Thus an engine working at maximum power may be used to haul a relatively light load at a high speed or a heavy load at a slow speed.
§ 4. Analysis of Train Resistance.—Train resistance may be analysed into the following components:—
- (1) Journal friction and friction of engine machinery.
- (2) Wind resistance.
- (3) Resistance due to gradients, represented by Rg
- (4) Resistance due to miscellaneous causes.
- (5) Resistance due to acceleration, represented by Ra.
- (6) Resistance due to curves.
The sum of all these components of resistance is at any instant equal to the resistance represented by R. At a uniform speed on a level straight road 3, 5 and 6 are zero. The total resistance is conveniently divided into two parts: (1) the resistance due to the vehicles hauled by the engine, represented by Rv; (2) the resistance of the engine and tender represented by Re. In each of these two cases the resistance can of course be analysed into the six components set out in the above list.
§ 5. Vehicle Resistance and Draw-bar Pull.—The power of the engine is applied to the vehicles through the draw-bar, so that the draw-bar pull is a measure of the vehicle resistance. The draw-bar pull for a given load is a function of the speed of the train, and numerous experiments have been made to find the relation connecting the pull with the speed under various conditions. The usual way of experimenting is to put a dynamo meter car (see Dynamometer) between the engine and the train. This car is equipped with apparatus by means of which a continuous record of the draw-bar pull is obtained on a distance base; time indications are also made on the diagram from which the speed at any instant can be deduced. The pull recorded on the diagram includes the resistances due to acceleration and to the gradient on which the train is moving. It is usual to subtract these resistances from the observed pull, so as to obtain the draw-bar pull reduced to what it would be at a uniform speed on the level. This corrected pull is then divided by the weight of the vehicles hauled, in which must be included the weight of the dynamometer car, and the quotient gives the resistance per ton of load hauled at a certain uniform speed on a straight and level road. A series of experiments were made by J. A. F. Aspinall on the Lancashire & Yorkshire railway to ascertain the resistance of trains of bogie passenger carriages of different lengths at varying speeds, and the results are recorded in a paper, “Train Resistance,” Proc. Inst. C.E. (1901), vol. 147. Aspinall’s results are expressed by the formula
| (12) |
where rv, is the resistance in pounds per ton, S is the speed in miles per hour, and L is the length of the train in feet measured over the carriage bodies. The two following expressions are given in the Bulletin of the International Railway Congress (vol. xii. p. 1275), by Barbier, for some experiments made on the Northern railway of France with a train of 157 tons mean weight; they are valid between 37 and 77 m. per hour:—
(13)
(14)
The Baldwin Locomotive Company give the formulae
(15)
and
(16)
All the above formulae refer to carriage stock. The resistance of goods wagons has not been so systematically investigated. In the paper above quoted Aspinall cites a case where the resistance of a train of empty wagons 1830 ft. long was 18·33 ℔ per ton at a speed of 26 m. per hour, and a train of full wagons 1045 ft. long gave only 9·12 ℔ per ton at a speed of 29 m. per hour. The resistance found from the above expressions includes the components 1, 2 and 4 of § 4. The resistance caused by the wind is very variable, and in extreme cases may double the resistance found from the formulae. A side wind causes excessive flange friction on the leeward side of the train, and increases the tractive resistances therefore very considerably, even though its velocity be relatively moderate. The curves corresponding to the above expressions are plotted in fig. 17, four values of L being taken for formula (12) corresponding to trains of 5, 10, 15 and 20 bogie carriages.
The resistance at starting is greater than the running resistance at moderate speeds. From Aspinall’s experiments it appears to be about 17 ℔ per ton, and this value is plotted on the diagram.
The resistance to motion round a curve has not been so systematically studied that any definite rule can be formulated applicable to all classes of rolling stock and all radii of curves. A general result could not be obtained, even from a large number of experiments, because the resistance round curves depends upon so many variable factors. In some cases the gauge is laid a little wider than the standard, and there are varying amounts of super elevation of the outer rail; but the most formidable factor in the production of resistance is the guard-rail, which is sometimes put in with the object of guiding the wheel which runs on the inner rail of the curve on the inside of the flange.
§ 6. Engine Resistance.—From experiments made on the North-Eastern railway (see a paper by W. H. Smith on “Express Locomotive Engines,” Proc. Inst. Mech. Eng., October 1898), it appeared that the engine resistance was about 35% of the total resistance, and in the train-resistance experiments on the Lancashire & Yorkshire railway quoted above the engine resistance was also about 35% of the total resistance, thus confirming the North-Eastern railway results. Barbier (loc. cit.) gives as the formula for the engine resistance
(17)
where S is the speed in miles per hour. This formula is valid between speeds of 37 and 77 m. per hour, and was obtained in connexion with the experiments previously quoted on the Northern railway of France with an engine and tender weighing about 83 tons. Barbier’s formula is plotted in Fig. 17, together with a curve expressing generally the results of some early experiments on the Great Western railway carried out by Sir D. Gooch. The extension of the Barbier curve beyond the above limits in fig. 17 gives values which must be regarded as only very approximate.

Fig. 17
§ 7. Rate at which work is done against the resistances given by the curves in fig. 17.—When the weight of the engine and tender and the weight of the vehicles are respectively given, the rate at which work must be done in the engine cylinders in order to maintain the train in motion at a stated speed can be computed by the aid of the curves plotted in fig. 17. Thus let an engine and tender weighing 80 tons haul vehicles weighing 200 tons at a uniform speed on the level of 40 m. per hour. As given by the Barbier curves in fig. 17, the engine resistance at 40 m. per hour is 20 ℔ per ton, and the vehicle resistance 8·5 ℔ per ton at the same speed. Hence
| Engine resistance, | Re = | 80 × 20 = | 1600 ℔ |
| Vehicle resistance, | Rv = | 200 × 8·5 = | 1700 ” |
| Train resistance, | R = | 3300 ” |
The speed, 40 m. per hour, is equal to 58·6 ft. per second; therefore the rate of working in foot-pounds per second is 3300 × 58·6, from which I.H.P. = (3300 × 58·6)/550 = 354. This is the horse-power, therefore, which must be developed in the cylinders to maintain the train in motion at a uniform speed of 40 m. per hour on a level straight road with the values of the resistances assumed.
§ 8. Rate at which work is done against a gradient.—Gradients are measured either by stating the number of feet horizontally, G say, in which the vertical rise is 1 ft., or by the vertical rise in 100 measured horizontally expressed as a percentage, or by the number of feet rising vertically in a mile. Thus a gradient of 1 in 200 is the same as a half per cent. grade or a rise of 26·4 ft. per mile. The difference between the horizontal distance and the distance measured along the rail is so small that it is negligible in all practical calculations. Hence if a train is travelling up the gradient at a speed of V ft. per second, the vertical rise per second is V/G ft. If W₁ is the weight of the train in pounds, the rate of working against the gradient expressed in horse-power units is,
(18)
Assuming the data of the previous section, and in addition that the train is required to maintain a speed of 40 m. per hour up a gradient of 1 in 300, the extra horse-power required will be
This must be exerted in addition to the horse-power calculated in the previous section, so that the total indicated horse-power which must be developed in the cylinders is now 354+223 = 577. If the train is running down a gradient this horse-power is the rate at which gravity is working on the train, so that with the data of the previous section, on the assumption that the train is running down a gradient of 1 in 300, the horse-power required to maintain the speed would be 354−223 = 131.
§ 9.—Rate at which work is done against acceleration.—If W₁ is the weight of the train in pounds and a the acceleration in feet per second, the force required to produce the acceleration is
(19)
And if V is the average speed during the change of velocity implied by the uniform acceleration a, the rate at which work is done by this force is
(20)
or in horse-power units
(21)
Assuming the data of § 7, suppose the train to change its speed from 40 to 41 m. per hour in 13 seconds. The average acceleration in feet per second is measured by the fraction
Therefore the horse-power which must be developed in the cylinders to effect this change of speed is from (21)
The rate of working is negative when the train is retarded; for instance, if the train had changed its speed from 41 to 40 m. per hour in 13 seconds, the rate at which work would have to be absorbed by the brake blocks would represent 237 H.P. This is lost in heat produced by the friction between the brake blocks and the wheels, though in some systems of electric driving some of the energy stored in the train may be returned to the central station during retardation. The principal condition operating in the design of locomotives intended for local services with frequent stops is the degree of acceleration required, the aim of the designer being to produce an engine which shall be able to bring the train to its journey speed in the shortest time possible. For example, suppose it is required to start a train weighing 200 tons from rest and bring it to a speed of 30 m. per hour in 30 seconds. The weight of the engine may be assumed in advance to be 80 tons. The acceleration, a, which may be supposed uniform, is 1·465. The average velocity is 15 m. per hour, which is equal to 22 ft. per second; therefore the tractive force required is, from (19),
(280×2240×1·465)/32 = 28,720 ℔,
and the corresponding horse-power which must be developed in the cylinders is, from (20), fV/550, and this is with f and V equal to the above values, 1149. To obtain the tractive force the weight on the coupled wheels must be about five times this amount—that is, 64 tons; and to obtain the horse-power the boiler will be one of the largest that can be built to the construction gauge. After acceleration to the journey speed of 30 m. per hour the horse-power required is reduced to about one-third of that required for acceleration alone.
§ 10. General expression for total rate of working.—Adding the various rates of working together
(22)
where We is weight of engine and tender in tons, Wv the weight of vehicles in tons, W the weight of train in tons = We + Wv, re, and rv the respective engine and vehicle resistances taken from the curves fig. 17 at a speed corresponding to the average speed during the acceleration a, G the gradient, g the acceleration due to gravity, and V the velocity of the train in feet per second. In this expression it is assumed that the acceleration is uniform, and this assumption is sufficiently accurate for any practical purpose to which the above formula would be applied in the ordinary working of a locomotive. If a is variable, then the formula must be applied in a series of steps, each step corresponding to a time interval over which the acceleration may be assumed uniform.
Dividing through by V and multiplying through by 550,
(23)
an expression giving the value of R the total tractive resistance. If the draw-bar pull is known to be Rv, then applying the same principles to the vehicle alone which above are applied to the whole train,
(24)
This expression may be used to find rv when the total draw-bar pull is observed as well as the speed, the changes of speed and the gradient. The speed held to correspond with the resistance must be the mean speed during the change of speed. The best way of deducing rv is to select portions of the dynamometer record where the speed is constant. Then a disappears from all the above expressions. These expressions indicate what frequent changes in the power are required as the train pursues its journey up and down gradients, against wind resistance, journal friction and perhaps the resistance of a badly laid track; and show how both the potential energy and kinetic energy of the train are continually changing: the first from a change in vertical position due to the gradients, the second from changes in speed. These considerations also indicate what a difficult matter it is to find the exact rate of working against the resistances, because of the difficulty of securing conditions which eliminate the effect both of the gradient and of acceleration.
§ 11. The Boiler.—Maximum Power.—The maximum power which can be developed by a locomotive depends upon the maximum rate of fuel combustion which can be maintained per square foot of grate. This maximum rate depends-upon the kind of coal used, whether small, friable, bituminous or hard, upon the thickness of the fire, and upon the correct design and setting of the blast-pipe. A limit is reached to the rate of combustion when the draught becomes strong enough to carry heavy lighted sparks through the tubes and chimney. This, besides reducing the efficiency of the furnace, introduces the danger of fire to crops and buildings near the line. The maximum rate of combustion may be as much as 150 ℔ of coal per square foot of grate per hour, and in exceptional cases even a, greater rate than this has been maintained. It is not economical to force the boiler to work at too high a rate, because it has been practically demonstrated that the boiler efficiency decreases after a certain point, as the rate of combustion increases. A few experimental results are set forth in Table XX., from which it will be seen that with a relatively low rate of combustion, a rate which denotes very light service, namely 28 ℔ of coal per square foot of grate per hour, the efficiency of the boiler is 82%, which is as good a result as can be obtained with the best class of stationary boiler or marine boiler even when using economizers.
The first group consists of experiments selected from the records of a large number made on the boiler of the locomotive belonging to the Purdue University, Indiana, U.S.A.
The second group consists of experiments made on a boiler belonging to the Great Eastern Railway Company. The first one of the group was made on the boiler fixed in the locomotive yard at Stratford, and the two remaining experiments of the group were made while the engine was working a train between London and March.
The third group consists of experiments selected from the records of a series of trials made on the London & South-Western railway with an express locomotive.
| Kind, and calorific value of coal. | Dry coal fired per square foot of grate per hour. ℔ |
Pounds of water evaporated per ℔ of coal from and at 212°F. |
Boiler efficiency. |
Reference. |
| Indiana block coal from the neighbourhood of Brazil. Estimated
calorific value, 13,000 B.Th.U. per ℔ |
49 109 181 |
7·83 6·59 5·71 |
0·58 0·49 0·42 |
Prof. Goss (Amer Soc. of Mech. Eng., vol. 22, 1900). |
| Nixon’s Navigation. Calorific value 15,560 B.Th.U. per ℔ | 35·5 28·1 31·7 |
13 13·3 13·1 |
0·82 0·82 0·81 |
“Experiments on Steam Boilers,” Donkin and Kennedy, (Engineer, London, 1897). |
| Calorific value, 13,903 | 62·5 | 11·15 | 0·77 | Adams and Pettigrew (Proc. Inst. C.E., vol. 125). |
| Calorific value, 12840 | 80·9 | 8·86 | 0·66 |
§ 12. Draught.—One pound of coal requires about 20 ℔ of air for its proper combustion in the fire-box of a locomotive, though this quantity of air diminishes as the rate of combustion increases. For instance, an engine having a grate area of 30 sq. ft. and burning 100 ℔ of coal per square foot of grate per hour would require that 60,000 ℔ of air should be drawn through the furnace per hour in order to burn the coal. This large quantity of air is forced though the furnace by means of the difference of pressure established between the external atmospheric pressure in the ash-pan and the pressure in the smoke-box.

Fig. 18.—Smoke-box, L. & N.W.R. four-coupled 6 ft. 6 in. passenger engine.
The exhaust steam passing from the engine through the blast pipe and the chimney produces a diminution of pressure, or partial vacuum, In the smoke-box roughly proportional to the weight of steam discharged per unit of time. The difference of pressure between the outside air and the smoke-box gases may be measured by the difference of the water levels in the limbs of a U tube, one limb being in communication with the smokebox, the other with the atmosphere. The difference of levels varies from 1 to as much as 10 in. in extreme cases. The draught corresponding to the smallest rate of combustion shown in Table XX. in Professor Goss’s experiments, was 1·72 in. of water, and for the highest rate, namely 181, 7·48 in. of water. To get the best effect the area of the blast-nozzle must be properly proportioned to the size of the cylinders and be properly set with regard to the base of the chimney. The best proportions are found by trial in all cases.
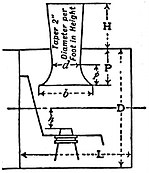
Figs. 18 and 19 show two smoke-boxes typical of English practice. Fig. 18 is the smoke-box of the 6 ft. 6 in. six-coupled express passenger engines designed by G. Whale for the London & North-Western Railway Company in 1904, and fig. 19 shows the box of the four-coupled express passenger engine designed by J. Holden for the Great Eastern Railway Company. In the case of the London & North-Western engine (fig. 18), the blast-pipe orifice B is placed at about the centre of the boiler barrel, and the exhaust steam is discharged straight into the trumpet—shaped end of the chimney, which is continued down inside the smoke-box. In fig. 19 the blast orifice B is set much lower, and the steam is discharged through a frustum of a cone set in the upper part of the smoke-box into the short chimney. Fig. 20 shows the standard proportions, recommended by the committee of the Railway Master Mechanics’ Association on Exhaust Pipes and Steam Passages (Proc. Amer. Railway Master Mechanics’ Assoc., 1906). According to the Report, for the best results both H and h should be made as great as practicable, and then d= 0·21D + 0·16h, b = 2d of 0·5D, P = 0·32D, p = 0·22D, L = 0·6D or 0·9D, but not of intermediate values. This last relation is, however, not well established. For much detailed information regarding American smoke-box practice, reference may be made to Locomotive Sparks, by Professor W. F. M. Goss (London, 1902).

Fig. 19.—Smoke-box and Spark Arrester, G.E.R. four-coupled express engine.
The arrangements for arresting sparks in American practice and on the continent of Europe are somewhat elaborate. In English practice where a spark-arrester is put in it usually takes the form of a wire-netting dividing the smoke-box horizontally into two parts at a level just above the top row of tubes, or arranged to form a continuous connexion between the blast-pipe and the chimney.
|
| Fig. 20.—Smoke-box, American Master Mechanics’ Association. |
Fig. 19 illustrates an arrangement designed by, J. Holden. The heavy sparks are projected from the tubes in straight lines and are caught by the louvres L, L, L, and by them deflected downwards to the bottom of the smoke-box, where they collect in a heap in the space D round a tube which is essentially an ejector. At every blast a small quantity of steam is caught by the orifice O and led to the ejectors, one on each side, with the result that the ashes are blown out into the receptacles on each side of the engine, one of which is shown at E. The louvres l, l, l are placed to shield the central region occupied by the blast-pipe.
As the indicated horse-power of the engine increases, the weight of steam discharged increases, and the smoke-box vacuum is increased, thereby causing more air to flow through the furnace and increasing the rate of combustion. Thus the demand for more steam is automatically responded to by the boiler. It is this close automatic interdependence of engine and boiler which makes the locomotive so extraordinarily well suited for the purpose of locomotive traction.
§ 13. The Steam Engine.—The steam engine of a locomotive has the general characteristics of a double-acting non-condensing engine (see Steam Engine). Distribution of steam is effected by a slide valve, sometimes fitted with a balancing device, and sometimes formed into a piston valve. All types of valves are with few exceptions operated by a link motion, generally of the Stephenson type, occasionally of the Allan type or the Gooch type, or with some form of radial gear as the Joy gear or the Walschaert gear, though the latter gear has characteristics which ally it with the link motions. The Stephenson link motion is used almost universally in England and America, but it has gradually been displaced by the Walschaert gear on the continent of Europe, and to some extent in England by the Joy gear. The general characteristics of the distribution effected by these gears are similar. Each of them, besides being a reversing gear, is an expansion gear both in forward and backward running. The lead is variable in the Stephenson link motion, whilst in the Walschaert and the Joy gears it is constant. Illustrations of these gears are given in the article Steam Engine, and the complete distribution of steam for both forward and backward running is worked out for a typical example of each of them in Valves and Valve Gear Mechanisms by W. E. Dalby (London, 1906).
§ 14. Cylinder Dimensions.—Adhesion.—Tractive Force.—A locomotive must be designed to fulfil two conditions. First, it must be able to exert a tractive force sufficient to start the train under the worst conditions possible on the railway over which it is to operate—for instance, when the train is stopped by signal on a rising gradient where the track is curved and fitted with a guard-rail. Secondly, it must be able to maintain the train at a given speed against the total resistances of the level or up a gradient of given inclination. These conditions are to a certain extent mutually antagonistic, since an engine designed to satisfy either condition independently of the other would be a different engine from that designed to make the best compromise between them.
Equation (3), § 1 expresses the fundamental condition which must be satisfied when a locomotive is starting a train. The torque exerted on the driving-axle by the steam engine just at starting may be that due to the full boiler pressure acting in the cylinders, but usually the weight on the coupled wheels is hardly sufficient to enable advantage to be taken of the full boiler pressure, and it has to be throttled down by the regulator to prevent slipping. Sand, driven between the wheel and the rail by a steam jet, used just at starting, increases the adhesion beyond the normal value and enables a larger pressure to be exerted on the piston than would otherwise be possible. When the train is started and is moving slowly, the torque acting on the driving-axle may be estimated as that due to about 85% of the full boiler pressure acting in the cylinders. The torque due to the two cylinders is variable to a greater or less extent, depending upon the degree of expansion in the cylinders and the speed. The form of the torque curve, or crank effort curve, as it is sometimes called, is discussed in the article Steam Engine, and the torque curve corresponding to actual indicator diagrams taken from an express passenger engine travelling at a speed of 65 m. per hour is given in The Balancing of Engines by W. E. Dalby (London, 1906).
The plotting of the torque curve is laborious, but the average torque acting, which is all that is required for the purposes of this article, can be found quite simply, thus:—Let p be the mean effective pressure acting in one cylinder, a, the area of the cylinder, and l, the stroke. Then the work done during one revolution of the crank is 2pla per cylinder. Assuming that the mean pressure in the other cylinder is also p, the total work done per revolution is 4pla. If T is the mean torque, the work done on the crank-axle per revolution is 2πT. Hence assuming the mechanical efficiency of the engine to be ε, and substituting; for the area a,
so that
But from § 1, T = ½DF; therefore
(25)
F in this expression is twice the average magnitude of the equal and opposite forces constituting the couple for one driving-wheel illustrated in fig. 16, one force of which acts to propel the train whilst the other is the value of the tangential frictional resistance between the wheel and the rail. This force F must not exceed the value μW or slipping will take place. Hence, if p is the maximum value of the mean effective pressure corresponding to about 85% of the boiler pressure,
(26)
is an expression giving a relation between the total weight on the coupled wheels, their diameters and the size of the cylinder. The magnitude of F when p and ε are put each equal to unity, is usually called the tractive force of the locomotive per pound of mean effective pressure in the cylinders. If p is the mean pressure at any speed the total tractive force which the engine is exerting is given by equation (25) above. The value of ε is variable, but is between ·7 and ·8, and for approximate calculations may be taken equal to unity. In the following examples the value will be assumed unity.
These relations may be illustrated by an example. Let an engine have two cylinders each 19 in. diameter and 26 in. stroke. Let the boiler pressure be 175 ℔ per square inch. Taking 85% of this, the maximum mean effective pressure would be 149 ℔ per square inch. Further, let the diameter of the driving-wheels be 6 ft. 3 in. Then the tractive force is, from (25),
Assuming that the frictional resistance at the rails is given by the weight on the wheels, the total weight on the driving-wheels necessary to secure sufficient adhesion to prevent slipping must be at least 8·3 × 5 = 41·5 tons. This would be distributed between three coupled axles giving an average of 1·38 tons per axle, though the distribution might not in practice be uniform, a larger proportion of the weight falling on the driving-axle. If the starting resistance of the whole tram be estimated at 16 ℔ per ton, this engine would be able to start 1·163 tons on the level, or about 400 tons on a gradient of 1 in 75, both these figures including the weight of the engine and tender, which would be about 100 tons.
The engine can only exert this large tractive force so long as the mean pressure is maintained at 149 ℔ per square inch. This high mean pressure cannot be maintained for long, because as the speed increases the demand for steam per unit of time increases, so that cut-off must take place earlier and earlier in the stroke, the limiting steady speed being attained when the rate at which steam is supplied to the cylinders is adjusted by the cut-off to be equal to the maximum rate at which the boiler can produce steam, which depends upon the maximum rate at which coal can be burnt per square foot of grate. If C is the number of pounds of coal burnt per square foot of grate per hour, the calorific value of which is c B.T .U. per pound, the maximum indicated horse-power is given by the expression
where A is the area of the grate in square feet, and η is the combined efficiency of the engine and boiler. With the data of the previous example, and assuming in addition that the grate area is 24 sq. ft., that the rate of combustion is 150 ℔ of coal per square foot of grate per hour, that the calorific value is 14000, and finally that η = 0·06, the maximum indicated horse-power which the engine might be expected to develop would be 0·06 × 150 × 14000 × 24 × 778/1980000 = 1190, corresponding to a mean effective pressure in the cylinders of 59·5 ℔ per square inch.
Assuming that the train is required to run at a speed of 60 m. per hour, that is 88 ft. per second, the total resistance R, which the engine can overcome at this speed, is by equation (10)
Thus although at a slow speed the engine can exert a tractive force of 18,600 ℔, at 60 m. per hour, the tractive force falls to 7400 ℔, and this cannot be increased except by increasing the rate of combustion (neglecting any small changes due to' a change in the efficiency η). Knowing the magnitude of R, the draw-bar pull, and hence the weight of vehicle the engine can haul at this speed, can be estimated if the resistances are known. Using the curves of fig. 17 it will be found that at 60 m. per hour the resistance of the engine and tender is 33 ℔ per ton, and the resistance of a train of bogie coaches about 14 ℔ per ton. Hence if W is the weight of the vehicles in tons, and the weight of the engine and tender be taken at 100 tons, the value of W can be found from the equation 14W + 3300 = 7440, from which W = 296 tons. This is the load which the engine would take in ordinary weather. With exceptionally bad weather the load would have to be reduced or two engines would have to be employed, or an exceptionally high rate of combustion would have to be maintained in the fire-box.
It will be seen at once that with a tractive force of 7400 ℔ a weight of 37,000 ℔ ( = 16·5 tons) would be enough to secure sufficient adhesion, and this could be easily carried on one axle. Hence for a level road the above load could be hauled at 60 m. per hour with a “single” engine. When the road leads the train up an incline, however, the tractive force must be increased, so that the need for coupled wheels soon arises if the road is at all a heavy one.
§ 15. Engine Efficiency. Combined Engine and Boiler Efficiency.—The combined engine and boiler efficiency has hitherto been taken to be 0·06; actual values of the boiler efficiencies are given in Table XX. Engine efficiency depends upon. many variable factors, such as the cut-off, the piston speed, the initial temperature of the steam, the final temperature of the steam, the, quality of the steam, the sizes of the steam-pipes, ports and passages, the arrangement of the cylinders and its effect on condensation, the mechanical perfection of the steam-distributing gear, the tightness of the piston, &c. A few values of the thermal efficiency obtained from experiments are given in Table XXI. in the second column, the first column being added to give some idea of the rate, at which the engine was working when the data from which the efficiency has been deduced were observed. The corresponding boiler efficiencies are given in the third column of the table, when they are known, and the combined efficiencies in the fourth column. The figures in this column indicate that 0·06 is a good average value to work with
| The number in this column refer to fig. 22. |
Indicated horsepower. |
Engine Efficiency. |
Boiler Efficiency. |
Combined Efficiency. |
Boiler Pressure ℔ per sq. in. |
|
| 128 205 222 399 |
0·073 0·075 0·080 0·088 |
Mean about 128 but throttled |
Deduced from data given by Professor Goss (Trans. Am. Soc. Mech. Eng. vol. 14). | |||
1 |
mean 129 |
0·057 |
0·815 |
0·047 |
mean about 120 |
Deduced from Kennedy and Donkin’s trials (Engineering London, 1887). |
| 2 3 |
490 582 |
0·098 0·11 |
0·775 0·665 |
0·077 0·073 |
167 169 |
Deduced from Adams and Pettigrew’s trials (Proc Inst. C. E. vol. 125). |
| 4 5 6 7 8 |
520 692 558 603 570 |
0·084 0·083 0·074 0·086 0·081 |
0·52 0·65 0·69 0·63 0·64 |
0·044 0·054 0·051 0·054 0·052 |
140 175 175 175 160 |
Deduced from Smith’s Experiments (Proc Inst. Mech. Eng. October 1898). |
It is instructive to inquire into the limiting efficiency of an engine consistent with the conditions under which it is working, because in no case can the efficiency of a steam-engine exceed a certain value which depends upon the temperatures at which it receives and rejects heat. Thus a standard of comparison for every individual engine may be obtained with which to compare its actual performance. The standard of comparison generally adopted for this purpose is obtained by calculating the efficiency of an engine working according to the Rankine cycle. That is to say, expansion is adiabatic and is continued down to the back pressure which in, a non-condensing engine is 14·7 ℔ per square inch, since any back pressure above this amount is an imperfection which belongs to the actual engine. The back pressure is supposed to be uniform, and there is no compression.

Fig. 21.
Fig. 21 shows the pressure-volume diagram of the Rankine cycle for one pound of steam where the initial pressure is 175 ℔ per square inch by the gauge, equivalent to 190 ℔ per square inch absolute. In no case could an engine receiving steam at the temperature corresponding to this pressure and rejecting heat at 212°F. convert more heat into work than is
represented by the area of this diagram. The area of the diagram may be measured, but it is usually more convenient to calculate the number of B.Th.U. which the area represents from the following formula, which is expressed in terms of the absolute temperature T1 of the steam at the steam-pipe, and the temperature T2 = 461° + 212° = 673° absolute corresponding to the back pressure:—
With the initial pressure of 190 ℔ per square inch absolute it will be found from a steam table that T1=838° absolute. Using this and the temperature 673° in the expression, it will be found that U = 185 B.Th.U. per pound of steam. If h2 is the water heat at the lower temperature, h1 the water heat at the higher temperature, and L1 the latent heat at the higher temperature, the heat supply per pound of steam is equal to h1 − h2+L1, which, from the steam tables, with the values of the temperatures given, is equal to 1013 B.Th.U. per pound. The thermal efficiency is therefore
That is to say, a perfect engine working between the limits of temperature assigned would convert only 18% of the total heat supply into work. This would be an ideal performance for an engine receiving steam at 190 ℔ initial pressure absolute, and rejecting steam at the back pressure assumed above, and could never be attained in practice. When the initial pressure is 100 ℔ per square inch by the gauge the thermal efficiency drops to about nearly 15% with the same back pressure. The way the thermal efficiency of the ideal engine increases with the pressure is exhibited in fig. 22 by the curve AB. The curve was drawn by calculating the thermal efficiency from the above expression for various values of the initial temperature, keeping the final temperature constant at 673°, and then plotting these efficiencies against the corresponding values of the gauge pressures.

Fig. 22.—Engine Efficiency Curves.
The actual thermal efficiencies observed in some of the cases cited in Table XXI. are plotted on the diagram, the reference numbers on which refer to the first column in the table. Thus the cross marked 3 in fig. 22 represents the thermal efficiency actually obtained in one of Adams and Pettigrew’s experiments; namely, 0·11, the pressure in the steam-pipe being 167 ℔ per square inch. From the diagram it will be seen that the corresponding efficiency of the ideal engine is about 0·18. The efficiency ratio is therefore 0·11/0·18 = 0·61. That is to say, the engine actually utilized 61% of the energy which it was possible to utilize by means of a perfect engine working with the same initial pressure against a back pressure equal to the atmosphere. Lines representing efficiency ratios of 0·6, 0·5 and 0·4 are plotted on the diagram, so that the efficiency ratios corresponding to the various experiments plotted may be readily read off. The initial temperature of the standard engine of comparison must be the temperature of the steam taken in the steam-pipe. For further information regarding the standard engine of comparison see the article Steam Engine and also the “Report of the Committee on the Thermal Efficiency of Steam Engines,” Proc. Inst; C.E. (1898).
§ 16. Piston Speed.—The expression for the indicated horse-power may be written
(27)
where v is the average piston speed in feet per second. For a stated value of the boiler pressure and the cut-off the mean pressure p is a function of the piston speed v. For the few cases where data are available—data, however, belonging to engines representing standard practice in their construction and in the design of cylinders and steam ports and passages—the law connecting p and v is approximately linear and of the form
(28)
where b and c are constants. (See W. E. Dalby, “The Economical Working of Locomotives,” Proc. Inst. C.E., 1905–6, vol. 164.) Substituting this value of p in (27)
(29)
the form of which indicates that there is a certain piston speed for which the I.H.P. is a maximum. In a particular case where the boiler pressure was maintained constant at 130 ℔ per square inch, and the cut-off was approximately 20% of the stroke, the values c = 55 and b =0·031 were deduced, from which it will be found that the value of the piston speed corresponding to the maximum horsepower is 887 ft. per minute. The data from which this result is deduced will be found in Professor Goss’s paper quoted above in Table XXI. The point is further- illustrated by some curves published in the American Engineer (June 1901) by G. R. Henderson recording the tests of a freight locomotive made on the Chicago & North-Western railway. Any modification of the design which will reduce the resistance to the flow of steam through the steam passages at high speeds will increase, the piston speed for which the indicated horse-power is a maximum.
§ 17. Compound Locomotives.—The thermal efficiency of a steam-engine is in general increased by carrying out the expansion of the steam in two, three or even more stages in separate cylinders, notwithstanding the inevitable drop of pressure which must occur when the steam is transferred from one cylinder to the other during the process of expansion. Compound working permits of a greater range of expansion than is possible with a simple engine, and incidentally there is less range of pressure per cylinder, so that the pressures and temperatures per cylinder have not such a wide range of variation. In compound working the combined volumes of the low-pressure cylinders is a measure of the power of the engine, since this represents the final volume of the steam used per stroke. The volume of the high-pressure cylinder may be varied within, wide limits for the same low-pressure volume; the proportions adopted should, however, be such that there is an absence of excessive drop between them as the steam is transferred from one to the other. Compound locomotives have been built by various designers, but opinion is still uncertain whether any commercial economy is obtained by their use. The varying load against which a locomotive works, and the fact that a locomotive is non-condensing, are factors which reduce the margin of possible economy within narrow limits. Coal-saving can be shown, to the extent of about 14% in some cases, but, the saving depends upon the kind of service on which the engine is employed. The first true compound locomotive was constructed in 1876 from designs by A. M. Mallet, at the, Creusot works in Bayonne. The first true compound, locomotive. in England was constructed at Crewe works in 1878 by F. W. Webb. It was of the same type as Mallet’s engine, and was made by simply bushing one cylinder of an ordinary two-cylinder simple engine, the bushed cylinder being the high-pressure and, the other cylinder the low-pressure cylinder. Webb evolved the type of three cylinder compound with which his name is associated in 1882. There were two high-pressure cylinders placed outside the frames and driving on a trailing wheel, and one low-pressure cylinder placed between the frames and driving on a wheel placed in front of the driving-wheel belonging to the high pressure cylinders. The steam connexions were such that the two high-pressure cylinders were placed in parallel, both exhausting into the one low-pressure cylinder. The first engines of this class were provided with high-pressure cylinders, 11 in. diameter and 24 in. stroke, a low-pressure cylinder 26 in. diameter, 24 in. stroke, and driving-wheels 6 ft. 6 in. diameter; but subsequently these dimensions were varied. There were no coupling rods. A complete account of Webb’s engines will be found in a paper, “The Compound Principle applied to Locomotives,” by E. Worthington, Proc, Inst. C.E., 1889, vol. xcvi. Locomotives have to start with the full load on the engine, consequently an outstanding feature of every compound locomotive is the apparatus or mechanism added to enable the engine to start readily. Generally steam from the boiler is admitted direct to the low-pressure cylinder through a reducing valve, and valves and devices are used to prevent the steam so admitted acting as a back pressure on the high-pressure cylinder. In the Webb compound the driver opened communication from the high-pressure exhaust pipe to the blast-pipe, and at the same time opened a valve giving a supply of steam from the boiler direct to the low pressure valve chest. T. W. Worsdell, developed the design of the two-cylinder compound in England and built several, first for the Great Eastern railway and subsequently for the North-Eastern railway. The engines were built on the Worsdell and Von Borries plan, and were fitted with an ingenious starting valve of an automatic character to overcome the difficulties of starting. Several compounds of a type introduced by W. M. Smith on the North-Eastern railway in 1898 have been built by the Midland railway. In these there are two low pressure cylinders placed outside the frame, and one high pressure cylinder placed between the frames. All cylinders drive on one crank-axle with three cranks at 120°. The driving wheels are coupled to a pair of trailing wheels. A controlling valve enables the supply of steam to the low-pressure cylinders to be supplemented by boiler steam at a reduced pressure. For a description and illustrations of the details of the starting devices used in the Webb, Worsdell and Smith compounds, see an article, “The Development of the Compound Locomotive in England,” by W. E. Dalby in the Engineering Magazine for September and October 1904. A famous type of compound locomotive developed on the continent of Europe is the four-cylinder De Glehn, some of which have been tried on the Great Western railway. There are two high-pressure cylinders placed outside the frame, and two low-pressure placed inside the frames. The low-pressure cylinders drive on the leading crank-axle with cranks at right angles, the high pressure cylinders driving on the trailing wheels. The wheels are coupled, but the feature of the engine is that the coupling rods act merely to keep the high-pressure and low-pressure engines in phase with one another, very little demand being made upon them to transmit force except when one of the wheels begins to slip. In this arrangement the whole of the adhesive weight of the engine is used in the best possible manner, and the driving of the train is practically equally divided between two axles. The engine can be worked as a four-cylinder simple at the will of the driver. S. M. Vauclain introduced successful type of four-cylinder compound in America in 1889. A high- and low-pressure cylinder are cast together, and the piston-rods belonging to them are both coupled to one cross-head which is connected to the driving-wheels, these again being coupled to other wheels in the usual way. The distribution of steam to both cylinders is effected by one piston-valve operated by a link motion, so that there is considerable mechanical simplicity in the arrangement. Later Vauclain introduced the “balanced compound.” In this engine the two piston-rods of one side are not coupled to a common cross-head, but drive on separate cranks at an angle of 180°, the pair of 180° cranks on each side being placed at right angles.
§ 18. The Balancing of Locomotives.—The unbalanced masses of a locomotive may be divided into two parts, namely, masses which revolve, as the crank-pins, the crank-cheeks, the coupling rods, &c.; and masses which reciprocate, made up of the piston, piston-rod, cross-head and a certain proportion of the connecting-rod. The revolving masses are truly balanced by balance weights placed between the spokes of the wheels, or sometimes by prolonging the crank-webs and forming the prolongation into balance weights. It is also the custom to balance a proportion of the reciprocating masses by balance weights placed between the spokes of the wheels, and the actual balance weight seen in a driving-wheel is the resultant of the separate weights required for the balancing of the revolving parts and the reciprocating parts. The component of a balance weight which is necessary to balance the reciprocating masses introduces a vertical unbalanced force which appears as a variation of pressure between the wheel and the rail, technically called the hammer-blow, the magnitude of which increases as the square of the speed of the train. In consequence of this action the compromise is usually followed of balancing only ⅔ of the reciprocating masses, thus keeping the hammer-blow within proper limits, and allowing ⅓ of the reciprocating masses to be unbalanced in the horizontal direction. It is not possible to do anything better with two-cylinder locomotives unless bob weights be added, but with four-cylinder four-crank engines complete balance is possible both in the vertical, and in the horizontal directions. When the four cranks are placed with two pairs at 180°, the pairs being at 90°, the forces are balanced without the introduction of a hammer-blow, but there remain large unbalanced couples, which if balanced by means of revolving weights in the wheels again reintroduce the hammer blow, and if left unbalanced tend to make the engine oscillate in a horizontal plane at high speed. The principles by means of which the magnitude and position of balance weights are worked out are given in the article Mechanics (Applied Mechanics), and the whole subject of locomotive balancing is exhaustively treated with numerous numerical examples in The Balancing of Engines by W. E. Dalby, London, 1906.
§ 19. Classification.—Locomotives may be classified primarily into “tender engines” and “tank engines,” the water and fuel in the latter being carried on the engine proper, while in the former they are carried in a separate vehicle. A tender is generally mounted on six wheels, or in some cases on two bogies, and carries a larger supply of water and fuel than can be carried by tanks and the bunker of a tank engine. A tender, however, is so much dead-weight to be hauled, whilst the weight of the water and fuel in a tank engine contributes largely to the production of adhesion. A classification may also be made, according to the work for which engines are designed, into passenger engines, goods engines, and shunting or switching engines. A convenient way of describing any type of engine is by means of numerals indicating the number of wheels—(1) in the group of wheels supporting the leading or chimney end, (2) in the group of coupled wheels, and (3) in the group supporting the trailing end of the engine. In the case where either the leading or trailing group of small wheels is absent the numeral 0 must be used in the series of three numbers used in the description. Thus 4–4–2 represents a bogie engine with four-coupled wheels and one pair of trailing wheels, the well known Atlantic type; 4–2–2 represents a bogie engine with a single pair of driving-wheels and a pair of trailing wheels; 0–4–4 represents an engine with four-coupled, wheels and a trailing bogie, and 4–4–0 an engine with four-coupled wheels and a leading bogie. A general description of the chief peculiarities of various kinds of locomotives is given in the following analysis of types:—
(1) “Single-driver” type, 4–2–2 or 2–2–2. Still used by several railways in Great Britain for express passenger service, but going out of favour; it is also found in France, and less often in Germany, Italy, and elsewhere in Europe. It is generally designed as a 4–2–2 engine, but some old types are still running with only three axles, the 2–2–2. It is adapted for light, high-speed service, and noted for its simplicity, excellent riding qualities, low cost of maintenance, and high mechanical efficiency; but having limited adhesive weight it is unsuitable for starting and accelerating heavy trains.
(2) “Four-coupled” type, 4–4–0, with leading bogie truck, For many years this was practically the only one used in America for all traffic, and it is often spoken of as the “American” type. In America it is still the standard engine for passenger traffic, but for goods service it is now employed only on branch lines. It has been extensively introduced, both in Great Britain and the continent of Europe, for passenger traffic, and is now the most numerous and popular class. It is a safe, steady-running and trustworthy engine, with excellent distribution of weight, and it is susceptible of a wide range of adaptability in power requirements.
(3) “Four-coupled” three-axle type, 2–4–0. Used to some extent in France and Germany and considerably in England for passenger traffic of moderate weight. Engines of this class, with 78-inch driving wheels and the leading axle fitted with Webb’s radial axle-box, for many years did excellent work on the London & North-Western railway. The famous engine “Charles Dickens” was one of this class. Built in 1882, it had by the 12th of September 1891 performed the feat of running a million miles in 9 years 219 days, and it completed two million miles on the 5th of August 1902, having by that date run 5312 trips with express trains between London and Manchester.
(4) “Four-coupled” three-axle type, with trailing axle, 0–4–2. Used on several English lines for fast passenger traffic, and also on many European railways. The advantages claimed for it are: short coupling-rods, large and unlimited fire-box carried by a trailing axle, compactness, and great power for a given weight. Its critics, however, accuse it of lack of stability, and assert that the use of large leading wheels as drivers results in rigidity and produces destructive strains on the machinery and permanent way.
(5) “Four-coupled” type, with a leading bogie truck and a trailing axle, 4–4–2. It is used to a limited extent both in England and on the continent of Europe, and is rapidly increasing in favour in the United States, where it originated and is known as the “Atlantic” type. It has many advantages for heavy high-speed service, namely, large and well-proportioned boiler, practically unlimited grate area, fire-box of favourable proportions for firing, fairly low centre of gravity, short coupling-rods, and, finally, a combination of the safe and smooth riding qualities of the four-coupled bogie type, with great steaming capacity and moderate axle loads. Occasionally a somewhat similar type is designed with the bogie under the fire-box and a single leading axle forward under the smoke-box—an arrangement in favour for suburban tank engines. In still rarer cases both a leading and a trailing bogie have been fitted.
(6) “Six-coupled” with bogie, or “Ten-wheel” type, 4–6–0. A powerful engine for heavy passenger and fast goods service. It is used to a limited extent both in Great Britain and on the continent of Europe, but is much more common in America. The design combines ample boiler capacity with large adhesive weight and moderate axle loads, but except on heavy gradients or for unusually large trains requiring engines of great adhesion, passenger traffic can be more efficiently and economically handled by four-coupled locomotives of the eight-wheel or Atlantic types.
(7) “Six-coupled” total-adhesion type (all the weight carried on the drivers), 0–6–0. This is the standard goods engine of Great Britain and the continent of Europe. In America the type is used only for shunting. It is a simple design of moderate boiler power.
(8) “Six-coupled” type, with a leading axle, 2–6–0. This is of American origin, and is there known as the “Mogul.” It is used largely in America for goods traffic. In Europe it is in considerable favour for goods and passenger traffic on heavy gradients. The type is, however, less in favour than either the ten-wheel or the eight-coupled “Consolidation” for freight traffic.
(9) “Eight-coupled” total-adhesion type, 0–8–0; now found on a good many English railways, and common on the continent of Europe for heavy slow goods traffic. In America it is comparatively infrequent, as total-adhesion types are not in favour.
(10) “Eight-coupled” type, with a leading axle, 2–8–0. This originated in America, where it is termed the “Consolidation.” In the United States it is the standard heavy slow-speed freight engine, and has been built of enormous size and weight. The type has been introduced in Europe, especially in Germany, where the advantages of a partial-adhesion type in increased stability and a larger boiler are becoming appreciated. Occasionally the American eight-coupled type has a bogie instead of a single leading axle (4–8–0), and is then termed a “Twelve-wheeler,” or “Mastodon.”
(11) “Ten-coupled” type, with a leading axle, 2–10–0. This originated in America, where it is known as the “Decapod.” It is used to a limited extent for mountain-grade goods traffic, and has the advantage over the “Consolidation” or eight-coupled type of lighter axle loads for a given tractive capacity.
In addition to the foregoing list, various special locomotive types have been developed for suburban service, where high rates of acceleration and frequent stops are required. These are generally tank engines, carrying their fuel and water on the engine proper. Their boilers are of relatively large proportions for the train weight and average speed, and the driving wheels of small diameter, a large proportion of their total weight being “adhesive.” Other special types are in limited use for “rack-railways,” and operate either by engagement of gearing on the locomotive into a rack between the track rails, or by a combination of this and rail adhesion.

Figs. 23–26.
§ 20. Current Developments.—The demand of the present day is for engines of larger power both for passenger and goods service, and the problem is to design such engines within the limitations fixed by the 4 ft. 8½ in gauge and the dimensions of the existing tunnels, arches, and other permanent works. The American engineer is more fortunately situated than his English brother with regard to the possibility of a solution, as will be seen from the comparative diagrams of construction gauges, figs. 23, 24, 25, 26. Fig. 23 shows the construction gauge for the London & North-Western railway, fig. 24 that for the Great Western[1] railway, fig. 25 that for the Great Eastern railway, whilst fig. 26 gives a general idea of the American gauge in a particular case, generally typical, however, of the American limits. In consequence of this increasing demand for power, higher boiler pressures are being used, in some cases 225 ℔ per sq. in. for a simple two-cylinder engine, and cylinder volume is slightly increased with the necessary accompaniment of heavier loads on the coupled Wheels to give the necessary adhesion. Both load and speed have increased so much in connexion with passenger trains that it is necessary to divide the weight required for adhesion between three-coupled axles, and the type of engine gradually coming into use in England for heavy express traffic is a six-coupled engine with a leading bogie, with wheels which would have been considered small a few years ago for the speed at which the engine runs. The same remarks apply to goods engines. There is a general increase in cylinder power, boiler pressure and weight, and in consequence in the number of coupled axles. Not only are the load and speed increasing, but the distances run without a stop are increasing also, and to avoid increasing the size of the tenders, water-troughs, first instituted by J. Ramsbottom on the London & North-Western railway in 1859, have been laid in the tracks of the leading main lines of Great Britain. For local services where stoppages are frequent the demand is for engines capable of quickly
| No | Owning Railway. | Type. | Cylinders. | Diam of Driving Wheels. |
Weight (Ton=2240 ℔). | Grate Area. |
Total Heating Surface. |
Remarks. | ||||
| Position. | Diam. | Stroke. | Total of Engine. |
Total on Coupled Wheels. |
Total with Tender. | |||||||
| In. | In. | In. | Tons. | Tons. | Tons. | Sq. Ft. | Sq. Ft. | |||||
| “Rocket” (Liverpool & Manchester) | 0–2–2 | Outside | 8 | 16½ | 56½ | 4·25 | . . | 7·45 | 6 | 137·75 | In Victoria and Albert Museum, South Kensington. | |
| 1 | Caledonian | 4–4–0 | Inside | 19 | 26 | 78 | 51·70 | 34·65 | 96·7 | 23 | 1600 | “Dunalsitair III” (900) class. |
| 2 | London & South-Western | 4–4–0 | Inside | 18½ | 26 | 79 | 48·85 | 33·45 | 93·0 | 24 | 1500 | Fitted with cross-water tubes in fire-box giving 165 sq. ft. of heating surface. |
| 3 | Midland | 4–4–0 | Inside | 19 | 26 | 78½ | 58·5 | 38·75 | 104·4 | 28·4 | 1557 | Belpaire fire-box. Pressure 220 ℔ per sq. in. |
| 4 | Great Western | 4–6–0 | Outside | 18⅜ | 30 | 80½ | 72 | 54·8 | 112 | 27 | 2000 | Fitted with superheater contributing 360 sq. ft. of heating surface to the total. Boiler pressure 200 ℔ per sq. in. |
| 5 | Great Eastern | 4–4–0 | Inside | 19 | 26 | 84 | 50·3 | 33·20 | 85·35 | 21·3 | 1630 | Fitted with Holden’s system of liquid fuel. |
| 6 | London & North Western | 4–6–0 | Inside | 19½ | 26 | 75 | 65·75 | 46·75 | 102·75 | 25 | 1990 | Experiment class. Boiler pressure 185 ℔ per sq. in. |
| 7 | Great Western | 4–6–0 | 2 inside 2 outside |
14¼ | 26 | 80½ | 75·6 | 55·4 | 115·6 | 27 | 2076 | 4-cylinder simple. Fitted with superheater contributing 269 sq. ft. of heating surface to the total. Boiler pressure 225 ℔ per sq. in. |
| 8 | London & South-Western | 4–6–0 | 2 inside 2 outside |
16 | 24 | 72 | 73 | 51·5 | . . | 31·5 | 2727 | 4-cylinder simple. Working pressure 175 ℔ per sq. in. Fitted with cross tubes in fire-box. |
| 9 | Lancashire & Yorkshire | 4–4–2 | Inside | 19 | 26 | 87 | 58·75 | 35·0 | 89·41 | 26·05 | 2052 | Belpaire fire-box. |
| 10 | Great Northern | 4–4–2 | Outside | 19 | 24 | 78 | 58 | 31 | 99 | 26·75 | 1442 | 990 class. |
| 11 | North-Eastern | 4–4–2 | 2 inside 2 outside |
22 14½ |
26 | 85 | 53·6 | 39·15 | 116·2 | 29 | 1969 | |
| 12 | Highland | 4–6–0 | Outside | 19½ | 26 | 69 | 58·85 | 43·85 | 96·96 | 26 | 2050 | Steam pressure 200 ℔ per sq. in. |
| 13 | Midland | 4–4–0 | 2 L.-P. outside 1 H.-P. inside |
21 19 |
26 26 |
84 | 59·8 | 39·1 | 102·7 | 28·4 | 1458 | 3-cylinder compound. Working pressure 220 ℔ per sq. in. |
| 14 | Midland | 0–6–0 | Inside | 18½ | 26 | 63 | 43·8 | 43·8 | 84·95 | 21·1 | 1412 | 175 ℔ per sq. in. |
| 15 | North Eastern | 0–6–0 | Inside | 18½ | 26 | 55 | 34·4 | 34·4 | 82·05 | 20·0 | 1658 | |
| 16 | Caledonian | 4–6–0 | Outside | 18 | 26 | 60 | 60·4 | 45·9 | 98·4 | 21 | 2018 | Presure 175 ℔ per sq. in. |
| 17 | Lancashire & Yorkshire | 0–8–0 | Inside | 20 | 26 | 54 | 53·78 | 53·78 | 84·45 | 26·05 | 2038 | |
| 18 | Great Western | 4–4–2 | 2 H.-P. outside 2 L.-P. inside |
14·2 23·6 |
25·2 | 80·5 | 73·8 | 38·5 | 108·9 | 33·3 | 2755 | De Glenn compound. Boiler presure 227 ℔ per sq. in. |
| 19 | Chicago & Alton | 4–4–2 | Outside | 20 | 28 | 80 | 82·8 | 43·7 | 155 | 33·5 | 2696 | Balanced piston valves |
| 20 | Atchison, Topeka and Santa Fé | 4–4–2 | 2 outside 2 inside |
25 15 |
26 26 |
79 | 86·5 | 45·3 | 160 | 49.5 | 3215 | 4-cylinder balanced compound. Vauclain type. |
| 21 | Central of Georgia | 4–6–2 | Outside | 20 | 28 | 68 | 84·0 | 50·7 | 150 | 46.8 | 3357 | Balanced valve. |
| 22 | Pennsylvania | 2–6–0 | Outside | 20 | 28 | 62 | 71·43 | 62·09 | 125 | 30.2 | 2431·3 | |
| 23 | Chicago, Rock Island & Pacific | 2–8–0 | Outside | 23 | 30 | 63 | 88·8 | 79·2 | 147 | 49.7 | 2912 | |
| 24 | Atchison, Topeka and Santa Fé | 2–10–2 | Outside Outside |
19 32 |
32 32 |
57 | 128·4 | 104·5 | 201 | 58.5 | 4796 | Tandem compound. |
| 25 | Great Northern, U.S.A. | 2–6–6–2 | Outside Outside |
21½ 32 |
32 32 |
55 | 158·5 | 141 | 225 | 78 | 5658 | Driving-wheels divided into two groups of six-coupled wheels. Leading group drven by L.-P. cylinders, trailing group by H.-P. cylinders. Mallet type. |
| 26 | Erie Railroad | 0–8–8–0 | Outside Outside |
25 39 |
28 28 |
51 | 183 | 183 | . . | 100 | 6108 | Mallet type. |
| 27 | Argentine Great Western | 2–10–0 | Outside | 19½ | 28 | 51 | 79·5 | 70·8 | 124·7 | 36 | 2440 | 5 ft 6 in gauge. |
| 28 | Belgian State | 2–6–0 | 2 outside 2 inside |
17⅛ | 24 | 78 | 82·0 | 52·0 | . . | 32·4 | 1672 | 4-cylinder simple expansion. Pressure 205 ℔ per sq. in. |
| 29 | Nord | 4–4–2 | 2 outside 2 inside |
13·4 22 |
25·2 | 80·3 | 66·2 | 32·5 | 107·3 | 29·7 | 2368 | Serve tubes. Boiler pressure 235 ℔ per sq. in. |
| 30 | Est | 4–6–0 | 2 H.-P. outside 2 L.-P. inside |
13·78 21·65 |
25·2 | 70 | 62·4 | 48·7 | . . | 27·6 | 2155 | Serve tubes. |
| 31 | Austro-Hungarian State | 2–10–0 | 2 H.-P. inside 2 L.-P. outside |
14·56 24·80 |
28·34 | 57 | 77·2 | 67·4 | . . | 49·5 | 2777 | Fitted with superheater contributing 678 sq. ft. to the total |
| 32 | Nord | 6–2–2–6 | 2 outside 2 ouside |
15·75 22·8 |
26·8 | 57·2 | 100 | 71 | . . | 32·3 | 2660 | Articulated tank engine on two motor bogies mounted on a central girder, splayed at ends to take buffer beams. H.-P. cylinders drive one bogie, L.-P. the other. |
| 33 | Paris, Orleans | 4–6–0 | 2 outside 2 inside |
14·17 23·62 |
25·19 | 57 | 72·6 | 53 | 109·5 | 33·37 | 2577 | Serve tubes. Boiler pressure 235 ℔ per sq. in. |
| 34 | Italian State | 6–4–0 | 2 H.-P. on one side 2 L.-P. on other |
14·17 23·22 |
23·62 | 75·6 | 69·5 | 42·6 | 106 | 32·29 | 2217 | Serve tubes. Boiler pressure 220 ℔ per sq. in. |
| 35 | Austrian State | 2–6–2 | 2 H.-P. inside 2 L.-P. outside |
14·56 24·80 |
28·34 | 71·5 | 68·9 | 42·9 | 107·9 | 43·0 | 2775 | Boiler pressure 220 ℔ per sq. in. |
| 36 | Prussian State | 4–4–2 | 2 H.-P. inside 2 L.-P. outside |
14·17 22·04 |
23·62 | 78 | 61·0 | 29·9 | 107·9 | 29·0 | 2520 | Lenz double-beat equilibrium valves. Serve tubes. Boiler pressure 205 ℔ per sq. in. |
accelerating the train to the journey speed. The nature of this problem is illustrated by the numerical example in § 9. When the service is frequent enough to give a good power factor continuously, the steam locomotive cannot compete with the electric motor for the purpose of quick acceleration, because the motors applied to the axles of a train may for a short time absorb power from the central station to an extent far in excess of anything which a locomotive boiler can supply.
With regard to the working of the locomotive, J. Holden developed the use of liquid fuel on the Great Eastern railway to a point beyond the experimental stage, and used it instead of coal with the engines running the heavy express traffic of the line, its continued use depending merely upon the relative market price of coal and oil. Compound locomotives have been tried, as stated in § 17, but the tendency in England is to revert to the simple engine for all classes of work, though on the continent of Europe and in America the compound locomotive is largely adopted, and is doing excellent work. A current development is the application of superheaters to locomotives, and the results obtained with them are exceedingly promising.
The leading dimensions of a few locomotives typical of English, American and European practice are given in Table XXII.
(W. E. D.)
- ↑ At the beginning of 1908 the Great Western’s loading gauge on its main lines was widened to 9 ft. 8 in. from a height of 5 ft. above rail level.






































