TACHEOMETRY (from Gr. ταχύς, quick; μέτρον, a measure), a system of rapid surveying, by which the positions, both horizontal and vertical, of points on the earth’s surface relatively to one another are determined without using a chain or tape or a separate levelling instrument. The ordinary methods of surveying with a theodolite, chain, and levelling instrument (see Surveying) are fairly satisfactory when the ground is pretty clear of obstructions and not very precipitous, but it becomes extremely cumbrous when the ground is much covered with bush, or broken up by ravines. Chain measurements are then both slow and liable to considerable error; the levelling, too, is carried on at great disadvantage in point of speed, though without serious loss of accuracy. These difficulties led to the introduction of tacheometry, in which, instead of the pole formerly employed to mark a point, a staff similar to a level staff is used. This is marked with heights from the foot, and is graduated according to the form of tacheometer in use. The azimuth angle is determined as formerly. The horizontal distance is inferred either from the vertical angle included between two well-defined points on the staff and the known distance between them, or by readings of the staff indicated by two fixed wires in the diaphragm of the telescope. The difference of height is computed from the angle of depression or elevation of a fixed point on the staff and the horizontal distance already obtained. Thus all the measurements requisite to locate a point both vertically and horizontally with reference to the point Where the tachometer is centred are determined by an observer at the instrument without any assistance beyond that of a man to hold the staff.
The simplest system of tacheometry employs a theodolite without additions of any kind, and the horizontal and vertical distances are obtained from the angles of depression or elevation of Sublease two well-defined points on a staff at known heights from method. the foot, the staff being held vertically . In fig. 1 let T be the telescope of a theodolite centred] over the point C, and let AB be the staff held truly vertical on the ground at A. Let P and P′ be the two well-defined marks on the face of the staff,

Fig. 1.
both of them at known heights above A, and enclosing a distance PP′=s between them. Let α and β be the measured angles of elevation of P and P′, and let d be the horizontal distance TM of the staff from the theodolite, and h the height PM of P above T. Then since
P′M =d tan β and PM =d tan α,
we have s=P′M-PM=d(tan β-tan α).
Therefore d = stan β − tan α; h= s tan αtan β − tan α.
If TC, the height of the rotation axis of the telescope above the ground, =q, and if AP =p, then the height of A above C is h−p+g. If, as is usually the case, a number of points are determined from one station of the theodolite, and hi, ha, ha, &e., be the values of 11 for the different points Al, AZ, Aa, &e., then the difference of level of A1 and A2 will be hg-hi, that of A1 and A3 will be h3−h1, and so on. To ensure the essential condition that the staff is held vertical, it is usually provided with a small circular spirit-level, and the staff-holder must always keep the bubble in the centre of its run. No graduation of the staff is required beyond two well-defined black lines across the white face at P and P′, but the marks can be; very usefully supplemented by wings fastened on the two } sides of the staff, having their tops at right angles to the staff, at the same height as the points P and P', and forming a continuation of the black lines. A convenient length for the staff is 12 ft., with the point P 2 ft. from the foot, and the point P' at the top of) the staff, so that A s=10 ft.
With the above arrangement the staff can easily be read with a 5-inch theodolite at half a mile distance. But while it is frequently very useful to determine approximately points a long way off, the determinations will not be nearly so accurate as those of near points. Thus suppose that the distance of the staff is d, and the intercept on the staff is's, and suppose that the personal and instrumental error is 5a. (ar being the angle subtended by's at the telescope); then since
d = stan α, d(d)dα = −s1+tan2αtan2α, or . .
da T S 5"/dz " § (S2+d2)
Therefore δd, the distance error, is given by the equation δd=−δα(s2+d2)/s. But at distances of 5 chains or more s2 will be very small compared with d2 and may be neglected, so that δd =-51.112/5. Since δα may be considered as constant for all distances where the staff can be distinctly read, the distance error increases as the square of the distance. With small theodolites, where special care has not been given to the graduating and reading of the vertical circle, δα will probably amount to about 20″, At a quarter of a mile excellent work can be done. In carrying on a traverse line by this method with stations 10 or 12 chains apart, the theodolite being set up at points about midway between the stations, the probable distance error in a mile is about 312 ft., and the probable level error about 4 in. In 25 miles these probable errors would correspond to about 18 ft. and 20 in. respectively. This system of tacheometry is well adapted for distant readings, and from the great simplicity of the observations there is little likelihood of errors in the field. But the reduction work is rather heavier than is the case with some of the tachometers described below. Since the accuracy of the method depends entirely upon the accuracy with which the vertical angles are measured, it is advisable that the vertical circle should be as large as possible, very finely and accurately divided, and fitted with good verniers and microscopes.
In Eckhold's omnimeter the vertical circle of the theodolite is dispensed with, and a saving of reduction work is effected by reading, not the vertical angles themselves, but the tangents of the angles.
In the Ziegler-Hager tachograph the tangents are read not horizontally but vertically, and the arrangement is as follows:— In fig. 2 O is the axis of rotation of the telescope; mn is the axial line of a steel bolt, which carries on its top a knife-edge, on which the telescope rests by means of an agate plate. The bolt is carried by a slide in which it can be raised or lowered by a micrometer screw fitted with a graduated head. The slide plays between the vertical cheeks of a standard rigidly attached to the frame of the instrument, and it can be raised or lowered by a rack and pinion. The telescope, which rests on the knife-edge, follows the movement of the bolt. The slide carries on one side a vernier by which to read the divisions on a scale fixed to one of the vertical legs of the standard, and the zero point o of the scale is the point where the horizontal plane through O cuts the scale when the plane-table or upper plate of the theodolite is truly level. The scale is graduated in divisions, each of which is the T2, ¢@th part of the distance Oo, or h. The head of the micrometer screw which raises or lowers the steel bolt in the slide is graduated with a zero mark and with marks corresponding to a vertical movement of the knife-edge of 1100h, 150h, &c. The instrument is used as follows:-Let AB be the surface of the ground, and BC a staff held vertically at B, and let CB be produced to meet the horizontal line through O in M. Let the head of the micrometer screw be turned till the zero division is exactly under the pointer. Let p be the zero division on the staff, and let the slide and bolt be raised by the rack and pinion movement till the axis of the telescope is directed towards p. Let v be the point where the line Op cuts mn, and let the tangent reading ov be taken on the scale. Then let the telescope be lowered by the micrometer screw in the slide till the division on the head of the screw marked I is exactly under the pointer; the knife-edge of the bolt has then been lowered through a distance 'vt equal to h/100. Let q be the point on the staff where the line Ot cuts it, and let the reading at q be taken. Then since the triangles between O and mn and O and CM are similar to each other, and vtt is 1100th of Oo, therefore pq will be 1100th of OM, or OM =100 × pq. This gives the horizontal distance of the staff from O, and the vertical distance pM of p above O is OM tan MOp=OM × ov/Oo, and since ov has been read in

Fig. 2.
parts of which Oo contains 100, the distance pM is readily obtained. If the difference of elevation of B and A be required, the height pM must be reduced by 12B and increased by OA, both known quantities. By this arrangement the reduction work of the observations is rendered extremely simple, and can readily be performed ingfie held. The instrument is well adapted for use with the plane-table.
Tacheometers in which the horizontal distance of the staff from the telescope is deduced from the readings of the staff indicated by two fixed wires in the diaphragm of the telescope will S dl now be considered. In fig. 3 BC is a diaphragm fixed Stadia method. in a tube having fine horizontal wires at B and C. Let the end E of the tube be closed by a disk which has a minute hole at E, to which the eye can be applied. If P and D be the oints on a vertical staff at which the lines EB and EC are observed to cut the staff, so that the intercept PD is known, then from similar triangles ED = (EC/BC)PD, and since EC and BC are constant, ED varies as PD. If, for instance, PD has a certain observed value when the staff is held at a certain distance ED, and has exactly half that value when the staff is held at another distance ED′, then the distance ED′ is one-half of the distance ED, and so on in proportion. The distance ED can be instantly inferred from the readings of the staff, if the latter be suitably graduated. If, for example, it be desired to know the distance ED in yards, and by construction the proportion EC/BC=50, then the intercept on the staff at 1 yard from E would be 150th of a yard, or ·72 inch, the intercept at 2 yards from E would be 2X·72 inches, and so on. If therefore the staff be graduated with divisions of ·72 inch, and the intercept be 45 of such divisions, it would be inferred that the distance of the staff from E was 45 yards. The constant proportion EC/BC can be checked by measuring 100 yards from E and observing whether the intercept is exactly 100 divisions or not.
If it is not, the wire diaphragm must be shifted in the tube until it is. In figs. 3, 4, 5 and) 6 the distances are deduced from the readings of a central wire in the optical axis of the telescope and of a wire above it, for the sake of simplicity. The usual arrangement is to fit the diaphragm with a central wire and with one or two wires above and below it at equal distances from the central wire. The vertical angle of depression or elevation is fixed by directing the central wire to a well-defined division on the staff, and the distance of the staff is inferred from the readings given by the corresponding wires above and below the central wire.
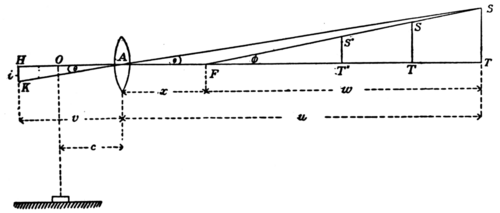
The elementary form of tachometer given above illustrates the general principle of the class of tachometers now under consideration, and as leading up to the practical form, in which the staff is viewed with a telescope mounted in the manner of a theodolite. The simplest form is Reichenbach's tachometer, which may be investigated as follows:—In fig. 4 let A be the object glass by which an image of the staff ST is formed at HK. The wire diaphragm is moved in the tube so as to coincide with the image,
and the image and wires are viewed with an eye-piece (not shown) in the usual way. Let O be the point where the vertical axis of the instrument cuts the axis of the telescope, the instrument being centred over a pe, from which the distance to the staff is required. The object glass fiif focal length = 𝑓) is at a distance 𝑐 from O. Let AT=𝑢 and AH=𝑣, and the angle SAT=HAK=θ. Then if 𝑖 be the height of the image HK, 𝑖=𝑣 tan θ. Since 1/𝑣+𝑖/𝑢=1/𝑓 we have 𝑣= -𝑢𝑓/(𝑢−Q, and hence i=uf tan θ/(𝑢−𝑓). Let F be some point on AT such that AF =𝑥 and FT =𝑢′. And let the angle SFT =φ. Then 𝑢 =𝑢′+𝑥 and tan θ=𝑢′ tan φ/(𝑢′+𝑥), and therefore
i= (𝑢′+𝑥)𝑓𝑢′+𝑥−𝑓 {=u, +x fé. tan¢=$tan 4>; and, if x=f, i=f tan ¢.
If therefore the point F be taken at a distance 𝑓 from the object glass, every intercept of the staff for positions between T and F, such as S′T′, S″T″, &c., which are bounded by the V line FS, and for which consequently θ is the same, will have the same height of image at the diaphragm. Conversely, if K be a wire in the diaphragm it will cut the image of the staff for all positions of the staff between T and F in points H object glass, were it not that the rays, after passing through the object glass, are received by the anal lat tic lens and the image of the staff is formed at K on the wire diaphragm, which is slid in the tube till it coincides with the position of the image. The image at K is viewed by an eye-piece in the usual way. Let T be the point where the image of the staff is cut by the central wire of the diaphragm, and S the point where the image is cut by one of the outer wires of the diaphragm. If 0 and ¢ be the angles subtended by ST at the object glass and at the point O respectively, and if i be the height of the image at K, h the height of the virtual image at H, then by elementary geometry and from optical considerations, we obtain i= f 1/f'f". » . -tan4>
"'(fi-d-hfz)"16f1'(C+f1)ld"J'2>i
Let fz be made such that of, -(c-{-fl) (d-f2)=0, the equation of condition above mentioned. Then fg ={d(c-l-fl) -cf1}/(C-|-fl). And i= .tan ¢= - tan ¢.
that lie on the line FS. Now the intercept S"T", half-way, L between F and T, will be one-half of ST, and therefore if the reading on the staff indicated by the wire in question be one-half of ST, it may be inferred that the position of the staff is half-way between F and T, and similarly for other distances. If the distance of ST from O is required, as is usually the case, a quantity f+c must be added to every distance from F determined as above.
It is very seldom that the line of sight AT of the telescope is at right angles to the staff. In general it is more or less inclined to the staff, which is almost always held vertical, and the horizontal and vertical distances of the staff from the axis of rotation of the telescope are found thus:—In fig. 5 let ST be the observed intercept on the staff when the telescope is inclined at an angle 𝑎 to the horizontal. Draw TS′ at right angles to OT. The angle TS′S will be very nearly a right angle, and STS′ may be taken as equal to 𝑎. If there were 𝑛 graduations (each corresponding to 1 yard in distance) in ST, there would be 𝑛 cos 𝑎 graduations in
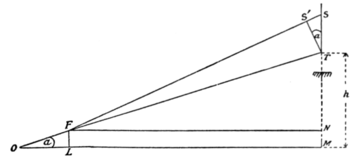
Fig. 5.
S′T, and therefore the distance of the staff from F, as inferred from the observed number of graduations in ST, must be multiplied by cos 𝑎. to give the true distance FT. Again FN =FT cos 𝑎, so that the distance inferred from the observed number of graduations in ST must be multiplied by cosza. to give the horizontal distance of F from T. To this must be added the distance OL=OF cos 𝑎(f+c) cos a to get the horizontal distance, OM, of O (the vertical axis of the instrument) from T. This value of OM must be multiplied by tan a to obtain the value of h, the vertical distance of T from O. Tables of the value of cos 𝑎, cos2 𝑎, and tan 𝑎 are necessary to facilitate these calculations.
In this tachometer the distances as inferred from the readings of the staff are the distances of the staff from F and not from O. This defect was remedied by Porro, who added a lens (called the anallattic lens) to the telescope. The arrangement of the telescope as manufactured by Messrs Troughton and Simms, is as follows:—In fig. 6 O is the point where the vertical axis of the instrument cuts the axis of the telescope. The object glass is fixed at a distance 𝑐 from O, and the anallattic lens at a distance 𝑑 from the object glass. The distances 𝑐 and 𝑑 are chosen to suit the constructive conveniences of the instrument. The diaphragm at K is movable so that it can be made to coincide with the image of the staff. The focal length 𝑓1 of the object glass is arbitrary, and the focal length 𝑓2 of the anallattic lens is determined from an equation of condition between 𝑐, 𝑑, 𝑓1, and 𝑓2. The image of the staff ST would be formed by the object glass at H, at a distance 𝑣1 from the
Therefore all the readings of the staff which would be given by the outer wire of the diaphragm will lie on the line OS (for all of which φ is the same), and the distance from O along OT will be proportional to the reading on the staff. Thus if the staff be suitably graduated, the distance from O can be immediately deduced from the reading. Also, as before, if the telescope be inclined at an angle at to the horizontal, the distance OT inferred from the number of graduations in ST must be multiplied by cos2 α, to give the horizontal distance of O from T, and the horizontal distance so obtained must be multiplied by tan α. to obtain the vertical distance of T from O.
The inconvenience of the reduction work necessary to obtain the horizontal and vertical distances produced the Wagner-Feunel tachometer, by which the distances can be read directly from the instrument. As is seen from fig. 7, three scales are provided, to measure the inclined distance, the horizontal distance, and the vertical distance respectively. All three are arranged in a plane parallel to the plane in which the telescope turns. The inclined scale is attached to the telescope exactly parallel to its line of collimation, and moves with it. The horizontal scale is fixed to the upper horizontal plate of the theodolite. The vertical scale is on the vertical edge of a right-angled triangle, which can be slid along on the top of the horizontal scale. The inclined scale carries a slide which is provided with two verniers. One of these is parallel to the inclined scale, and is for the purpose of setting off on the scale (in terms of the divisions on the scale) the inclined distance of the staff from the axis of rotation of the telescope. The other turns on a pivot whose centre is accurately in the edge of the inclined scale at the point where the zero division of the inclined vernier

Fig. 7.
cuts the edge, and is for the purpose of reading the vertical scale; it can be turned on its pivot so as to be vertical whatever may be the inclination of the telescope. Moreover, since the distance from the centre of the pivot to the zero of the vernier is always constant and known, the vertical scale can be graduated so that the reading of the vernier gives the height (in terms of the division on the scale) of the staff above the axis of rotation of the telescope. The horizontal scale attached to the horizontal plate of the theodolite is read by means of a vernier carried by the triangle. To ascertain the horizontal and vertical distances of the point on the staff which is cut by the middle wire in the diaphragm of the telescope from the rotation axis of the telescope, the inclined distance of the point on the staff is read by means of the wires, as in Porro's tachometer. This distance (in terms of the divisions) is then set off on the inclined scale by means of the inclined vernier, and the vertical scale on the triangle is moved up to the vertical vernier, which is adjusted to its edge. With proper graduation of the horizontal and vertical scales the horizontal and vertical distances can be at once read off on the scales. This method, however, requires that the staff be held so that its face is perpendicular to the line of sight, which is more troublesome than holding the staff vertical.
Authorities.—Brough on "Tacheometry," Proc. Inst. C.E., vol. xci. Pierce on the "Use of the, Plane Table," ibid. vol. xcii. Kennedy on the "Tacheometer," ibid. vol. xcix. Airy on the "Probable Errors of Surveying by Vertical Angles," ibid. vol. ci. Middleton on "Observations in Tacheometry," ibid. vol. cxvi. Young on " Surveying with the Omnimeter," ibid. vol. cxvii. J. Bridges Lee on "Photographic Surveying," Trans. Soc. Engin., vol. for 1899. "The Ziegler-Hager Tacheograph," Engineering, vol. lxv. (W. Ay.)