THERMOMETRY (Gr. θερμός, warm; μέτρον, a measure), the art of measuring temperature or degree of heat. The instruments used for this purpose are known as thermometers, or sometimes, when the temperatures to be measured are high, as pyrometers.
1. A brief sketch of the evolution of the thermometer is included in the article Heat, § 2 and 3. The object of the present article is to discuss the general principles on which the accurate measurement of temperature depends, and to describe the application of these principles to the construction and use of the most important types of thermometer. Special attention will be devoted to more recent advances in scientific methods of testing thermometers and to the application of electrical and optical methods to the difficult problem of measuring high temperatures. In the article Pyrometer an account will be found of some of the thermoscopic methods employed in the arts for determining high temperatures.
2. Zero: Fundamental Interval.—In all systems of measuring temperature it is necessary (1) to choose a zero or starting-point from which to reckon, (2) to determine the size of the degree by subdividing the interval between two selected fixed points of the scale (called the “fundamental interval”) into a given number of equal parts. The fundamental interval selected is that between the temperature of melting ice and the temperature of condensing steam, under standard atmospheric pressure. On the Centigrade system the fundamental interval is divided into 100 parts, and the melting-point of ice is taken as the zero of the scale. We shall denote temperature reckoned on this system by the letter t, or by affixing the letter C. It is often convenient to reckon temperature, not from the melting point of ice, but from a theoretical or absolute zero representing the lowest conceivable temperature. We shall denote temperature reckoned in this manner by the letter T, or θ, or by affixing the letters Abs. In practice, since the absolute zero is unattainable, the absolute temperature is deduced from the Centigrade temperature by adding a constant quantity, T0, representing the interval between the absolute zero and the melting-point of ice; thus T=t+T0.
3. Arbitrary Scales.—An arbitrary scale can be constructed by selecting any physical property of a substance which varies regularly with the temperature, such as the volume of a liquid, or the pressure or density of a gas, or the electrical resistance of a metal. Thus if V denote the volume of a given mass at the temperature t, and if V0, V1 represent the volumes of the same mass at the temperatures 0° and 100° C., the size of 1° C. on the scale of this arbitrary thermometer is one hundredth part of the fundamental interval, namely (V1−V0)/100, and the temperature t at volume V is the number of these degrees contained in the expansion V−V0 between 0° and t°C. We thus arrive at the formula
| t=100 (V−V0)/(V1−V0) | (1), |
which is the general expression for the temperature Centigrade on any such arbitrary scale, provided that we substitute for V the particular physical property selected as the basis of the scale. If we prefer to reckon temperature from an arbitrary zero defined by the vanishing of V, which may conveniently be called the fundamental zero of the scale considered, we have, putting V=0 in equation (1), the numerical values of the fundamental zero T0, and of the temperature T reckoned from this zero
| T0=100V0/(V1−V0), and T=T0V/V0=t+T0 | (2). |
It is frequently convenient to measure temperature in this manner when dealing with gases, or electrical resistance thermometers.
4. Absolute Scale.—It is necessary for theoretical purposes to reduce all experimental results as far as possible to the absolute scale, defined as explained in Heat, § 21, on the basis of Carnot's principle, which is independent of the properties of any particular substance. Temperature on this scale measured from the absolute zero will be denoted by the letter θ. This scale can be most nearly realized in practice by observing the temperature T on the scale of a gas-thermometer, and .making special experiments on the gas to determine how far its scale deviates from that of the thermodynamical engine. In the case of the gases hydrogen and helium, which can exist in the liquid state only at very low temperatures, the deviations from the absolute scale at ordinary temperatures are so small that they cannot be certainly determined. Thermometers containing these gases are generally taken as the ultimate standards of reference in practical thermometry.
Mercurial Thermometry
5. The most familiar type of thermometer depends on the apparent expansion of a liquid hermetically sealed in a glass bulb attached to a graduated stem of fine bore. Of all liquid-in-glass thermometers those containing mercury are almost invariably selected for scientific purposes, although at first sight mercury would appear to be the least suitable liquid, on account of its small coefficient of expansion. The smallness of the expansion necessitates an extremely fine bore for the stem, which introduces errors in consequence of the high surface tension of mercury. The considerable density of the liquid also tends to exaggerate the effects of change of position due to variation of the pressure exerted on the interior of the bulb by the liquid column. These errors are small and fairly regular, and can be corrected within certain limits. A much more serious source of trouble, especially at high temperatures, is the imperfect elasticity of the glass, which causes more or less irregular changes in the volume of the bulb. The effect of these changes on the readings of the thermometer is enhanced by the smallness of the expansion of mercury, and might be reduced by employing a more expansible liquid. It is more likely, however, that the defect will be remedied by the construction of thermometers of fused quartz, which is the most perfectly elastic solid hitherto discovered. For work at low temperatures the range of a mercury thermometer is limited by its freezing-point (−39° C.).
These are the serious disadvantages attending the use of mercury, but in other respects it possesses so many advantages over alcohol or other substitutes, that it will in all probability continue to be used almost exclusively in thermometers of this type for scientific work. Among its chief advantages may be reckoned its high boiling-point (357° C.), and the absence of evaporation from the top of the thread, which is so serious a source of error with the alcohol thermometer. With mercury the evaporation is almost inappreciable at 100° C., and can in all cases be avoided by exposing the upper parts of the emergent thread to the temperature of the air. Although an evacuated mercury thermometer cannot be safely used at temperatures over 300° C., owing to the breaking up of the thread of liquid in the stem, it' has been found possible, by filling the upper part of the stem with nitrogen or carbon dioxide under high pressure, to extend the range to 550° C. A more important advantage for accurate work is the fact that mercury does not wet glass, and avoids any possible errors due to adherent films of liquid on the walls of the tube. This greatly facilitates observations, and also renders it possible to calibrate the thermometer after construction, which cannot be satisfactorily accomplished with other liquids. The process of construction and calibration is further facilitated by the fact that mercury does not dissolve air to any appreciable extent. In consequence of the regularity of expansion of mercury at ordinary temperatures, the scale of the mercury thermometer agrees very closely with that of the gas thermometer. The liquid is very easily obtained in a high state of purity by distillation, and has practically no chemical action on glass. In this respect it is superior to the liquid alloy of potassium and sodium, which has been employed in some high-temperature thermometers, but which rapidly reduces silica at high temperatures. The high conductivity and low specific heat of mercury as compared with most other liquids tend to render the thermometer quick and sensitive in action. Its opacity considerably facilitates accurate reading, and even the smallness of its expansion has one great countervailing advantage, in that the correction for stem-exposure is proportionately reduced. This correction, which (even in the case of mercury) may amount to as much as 40° C. at 550° C., is far the most uncertain in its application, and is the most serious objection to the use of the liquid-in-glass thermometer at high temperatures.
6. Construction.—The construction of the most accurate type of mercury thermometer has undergone some changes of detail in recent years. The range of the most accurate standards is generally restricted to the fundamental interval. The length of a degree on the stem can be increased to any extent by enlarging the bulb or diminishing the bore of the stem, but it is found in practice that there is no advantage in making the scale more open than one centimetre to the degree C. in standard instruments, or in increasing the number of divisions beyond ten or at most twenty to the degree. Enlarging the bulb makes the instrument sluggish, and exaggerates the errors due to imperfect elasticity. Diminishing the bore of the tube increases the errors due to capillary friction. Even one centimetre to the degree is an impracticable scale for thermometers graduated continuously from 0° to 100° C., owing to the excessive length of the stem. In order to secure so open a scale, it is necessary to limit the range to 35°, or at most 50°. The fixed points 0° and 100° may still be retained, for purposes of testing and reference, by the device, now commonly employed, of blowing auxiliary bulbs or ampoules on the stem, the volume of which is carefully adjusted to correspond with the number of degrees that it is desired to suppress.
In the best instruments for Work of precision the bulb is not blown on the capillary tube itself, but is formed of a separate piece of tube fused on the stem. It is possible in this manner to secure greater uniformity of strength and regularity of dimensions. The thickness of the glass is generally between half a millimetre and one millimetre. The advantage in point of quickness gained by making the glass thin is more than counterbalanced by increased fragility and liability to distortion. The best form of bulb is cylindrical, of the same external diameter as the stem. The bore of the stem should also be cylindrical, and not oval or flattened, in order to diminish errors due to capillarity, and to secure the greatest possible uniformity of section. The glass should be clear, and not backed with opal, both to admit of reading from either side, and to minimize risk of bending or distortion. In the commoner sorts of thermometers, which are intended for rough purposes and to be read without the application of minute corrections, it is not unusual to divide the tube into divisions of equal volume by a preliminary calibration. In the most accurate instruments it is preferable to divide the tube into divisions of equal length, as this can be more accurately effected., The corrections to be applied to the readings to allow for inequalities of bore can be most satisfactorily determined in the case of mercury thermometers by calibrating the tube after the instrument is completed (see Calibration). This correction is known as the “calibration correction.” Instead of being separately determined it may be included in the scale correction by comparison with a standard instrument, such as a platinum-resistance thermometer.
7. Corrections.—The corrections to be applied to the readings of a mercury thermometer, in addition to the calibration correction, may be summarized under the following heads: (i.), Zero. (ii.) Fundamental Interval. (iii.) Internal and External Pressure. (iv.) Stem Exposure. (v.) Scale Correction, including Poggendorff’s correction.
(1) The changes of zero are of two kinds. (a) Secular rise of zero due to gradual recovery from changes or strains acquired by the bulb during the process of manufacture. This process may be hastened and subsequent changes practically eliminated by annealing the bulb after manufacture, and before final adjustment, at a high temperature, such as that of boiling sulphur (about 450° C.). A thermometer which has not been so treated may show a rise of zero amounting to as much as 20° or 30° when exposed for some time to a temperature of 350° C. (b) Temporary depression of zero after each exposure to a high temperature, followed by a slow recovery which may last for days or weeks. The best thermometers of hard glass show a depression of zero amounting to about one-tenth of 1° C. after exposure to 100° C. In softer glass the depression is usually greater and more persistent, and may amount to half a degree after 100° C. At higher temperatures the depression generally increases roughly as the square of the temperature above 0° C. It may amount to 2° or 3° at 300° C. The effect cannot be calculated or predicted in any series of observations. because it depends in so complicated a manner on the past history and on the time. It is a most serious difficulty in accurate mercurial thermometry, especially at high temperatures. The most satisfactory method of correction appears to be to observe the zero immediately after each reading. and to reckon the temperature from the variable zero thus observed. The rationale of this procedure is that the depression is produced at the high temperature much more rapidly than the subsequent recovery at the low temperature. The thermometer is taken from the bath and allowed to cool rapidly by free exposure to the air. As soon as it reaches 40° or 50° C., it is plunged in the melting ice, and the lowest point reached is taken as the temporary zero.
The following formulae have been proposed by various observers to represent the depression of zero for different kinds of glass:—
| Pernet, French cristal, dz=0·0040(t/100)2 . . . . | . (4) |
| Guillaume, Verre dur, 0–100° C., dz=(8886t+10·84t 2)10−7 | |
| Bottcher, Cristal dur, 0–190° C., dz= (7970t+329t 2)10−7 | |
| ,, Jena, 16, iii., dz=(7100t−8t 2) 10−7 . . . . |
 |
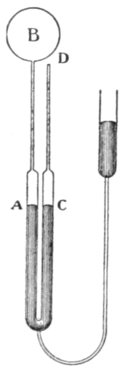
| Fig. 1.—Hypsometer. |
The symbol dz in these formulae stands for the depression of zero produced by an exposure to a temperature t. The depression is about three times as large in French crystal as in English flint glass, and varies roughly as the square of t. Verre dur and Jena, 16, iii., are varieties of hard glass chosen as standards in France and Germany respectively, on account of the comparatively small depression of zero to which they are liable. At low temperatures, up to 50° C., the depression is very nearly proportional to t, but at temperatures above 100° C. it is necessary to adopt another formula in which the term depending upon t 2 is more important. These formulae are useful as giving an idea of the probable size of thee corrections any case, but they cannot be employed in practice except in the simplest cases and at low temperatures. On account of these temporary changes of zero, a mercury thermometer intended for the most accurate work at ordinary temperatures (as in calorimetry) should preferably never be heated above 40° or 50° C., and certainly never above 100° C. Above 100° C. the changes of zero become more irregular and more variable, depending on the rate of cooling and on the sequence of previous observations, so that even if the method of observing the zero after each reading is adopted, the order of precision attainable rapidly diminishes.
(II) Fundamental Interval.—The thermometer to be tested is exposed to steam condensing at atmospheric pressure in an apparatus which is often called a “hypsometer,” constructed with double walls to protect the inner tube containing the thermometer from any cooling by radiation. The standard atmospheric pressure at which the temperature of the steam is by definition if equal to 100° C. is equivalent to that produced by a column of mercury at 0° C. and 760 millimetres high, the force of gravitation being equal to that at sea-level in latitude 45°. The atmospheric pressure at the time of observation is reduced to these units by applying the usual corrections for temperature and gravitation. If the pressure is near 760 mm., the temperature of the steam may be deduced by assuming that it increases at the rate of 1° C. for 27·2 mm. of pressure. If the pressure is not near 760 mm., the application of the correction is less certain, but is generally taken from Regnault’s tables, from which the following data are extracted. Thermometers cannot be satisfactorily tested at an elevated station where the height of the barometer H is less than 700 mm., as the steam point is too uncertain.
A convenient type of hypsometer is shown in fig. 1. The boiler B is separate from the steam-jacket A surrounding the thermometer. A gauge G is provided for indicating the steam pressure (difference from atmospheric) and a condenser C for returning the condensed steam to the boiler. The thermometer is observed by the microscope M.
| Pressure (corrected) | 790 | 780 | 770 | 760 | 750 | 740 | 730 | 720 | 710 |
| Steam temp. = 100° C., + | +1·083 | +·726 | +·365 | 0 | −·369 | −·742 | −1·120 | −1·502 | −1·888 |
| Approximate formula dt1=0·0367(H−760)−·000020(H−760)2 | (5) |
If the barometer has a brass scale correct at 0° C., and H be the reading in millimetres, the correction for temperature is made approximately by subtracting 0·00163 H mm.
If L is the latitude and M the height of the station in metres above the sea-level, the correction for gravitation is approximately made by subtracting (0·0026 cos 2L+0·0000002M) H mm.
The zero of the thermometer is observed immediately after the steam point. If n be the interval in degrees of the scale between the two observations, and if t1 be the temperature of the steam, the fundamental interval of the thermometer may be taken as 100 n/t1, provided that t1 is nearly 100° C. Since all the readings of a thermometer have to be corrected for the error of the fundamental interval, by dividing by the fundamental interval thus observed and multiplying by 100, it is a matter of some convenience in practice to have the instrument graduated so that the difference between the readings in ice and at 100° C. is very nearly 100° of the stem. The correction can then be applied as a small percentage independently of the other corrections. The method of determining the fundamental interval above described applies to all other kinds of thermometers, except that it is not generally necessary to observe the zero after the steam point. The temperature of the steam t1 should be expressed in the scale of the thermometer tested, if the scale differs appreciably from that of Regnaut.
(III) Pressure Correction.—The corrections for variations of internal and external pressure on the bulb are of some importance in accurate thermometry, but can be applied with considerable certainty at moderate temperatures. The correction for external pressure is assumed to be proportional to the change of pressure, and to be independent of the temperature. It is generally determined by enclosing the thermometer to be tested in a vessel of water, and observing the change of reading on exhausting or readmitting the air. The correction is generally between one and two thousandths of a degree per centimetre of mercury change of pressure, but must be determined for each thermometer, as it depends on the nature of the glass and on the form and thickness of the walls of the bulb. The coefficient of the correction for internal pressure is greater than that for external pressure by the difference between the compressibility of mercury and that of glass, and may be calculated from it by assuming this relation. If b0, b1, are the external and internal coefficients, expressed in degrees of temperature per centimetre of mercury, we have the relation
| b1=b0+0·00015, degrees per cm. of mercury | (6) |
The coefficient of internal pressure can also be determined by taking readings in the horizontal and vertical positions when the thermometer is at some steady temperature such as that of ice or steam. The reading of the thermometer is generally reduced to an external pressure of one standard atmosphere, and to an internal pressure corresponding to the horizontal position. It is also. possible to include the internal pressure correction in the scale correction, if the thermometer is always read in the vertical position. In addition to the variations of internal pressure due to the column of mercury in the Stem, there are variations due to capillarity. The internal pressure is greater when the mercury is rising than when it is falling, and the reading is depressed to an extent depending on the fineness of the bore and the thinness of the walls of the bulb. The capillary pressure does not depend only on the bore of the tube, but also apparently to an even greater extent on the state of the walls of the tube. The least trace of dirt on the glass or on the mercury is capable of producing capillary pressures much greater than would be calculated from the diameter of the tube. Even in the best thermometers, when there are no inequalities of bore sufficient to account for the observed variations, it is seldom found that the mercury runs equally easily in all parts of the stem. These variations of capillary pressure are somewhat capricious, and set a limit to the order of accuracy attainable with the mercury thermometer. It appears that the difference of reading of a good thermometer between a rising and falling meniscus may amount to five or ten thousandths of a degree. The difference may be reduced by continuous tapping, but it is generally best to take readings always on a rising column, especially as the variations in the angle of contact, and therefore in the capillary pressure, appear to be much smaller for the rising meniscus. In ordinary work the zero reading and the steam reading would both generally correspond to a falling meniscus; the former necessarily, the latter on account of the phenomenon of the temporary depression of zero, which causes the thermometer to read higher during the first moments of its exposure to steam than it does when the expansion of the bulb has reached its limit. It is easy to secure a rising meniscus at the steam point by momentarily cooling the thermometer. At the zero point the meniscus generally begins to rise after five or ten minutes. The question, however, is not of much importance, as the error, if any, is regular, and the correction for capillarity is necessarily uncertain.
(IV) Stem-Exposure Correction.—When the bulb of a mercury thermometer is immersed in a bath at a temperature t, and a part of the column of mercury having a length of n degrees is exposed to a lower temperature t2, the reading of the thermometer will be lower by a✕n✕(t−t2) degrees (nearly) than it would have been if the whole of the mercury and stem had been at the temperature l. The factor a in this expression is the apparent coefficient of expansion of mercury in glass, and varies from ·000150 to ·000165 for different kinds of glass. In order to apply this correction, it is usual to observe t2 by means of an auxiliary “stem-thermometer” with its bulb placed near the middle of the emergent column n. Occasionally stem-thermometers with long thin bulbs are employed to give more nearly the average temperature of the whole emergent column. Owing to conduction along the stem of the thermometer, and to heated vapours near the bath, the mean temperature determined in this manner is generally too low. To allow for this empirically, an arbitrary reduction is often made in the value taken for n or a, but this cannot be regarded as satisfactory for work of precision. The only practical method of reducing the correction is to limit the number of degrees n exposed, or, in other words, to work with thermometers of “limited range.” Each of these thermometers must then be corrected by comparison with a standard thermometer free from stem-exposure correction, such as a platinum-resistance thermometer. To secure results of any value the correction must be determined at each point under the actual conditions of observation under which the thermometer is to be used. In work of precision it is necessary to use ten or twenty thermometers to cover a range of 300°, as this is the only method of securing an open scale and reasonable accuracy as regards stem-exposure. To quote the opinion of C. E. Guillaume, one of the leading authorities on mercurial thermometry: “When this correction is large, it cannot generally be determined with sufficient approximation for measurements of precision. The mercury thermometer should then be replaced by other instruments, among which those based on the variation of the electrical resistance of metals hold the first rank.”
(V) Scale Correction.—The correction required to reduce the readings of a mercurial thermometer to the normal scale may appropriately be called the “ scale correction.” One of the chief advantages of the mercurial thermometer for scientific purposes is that its scale agrees very closely with the thermodynamical scale between 0° and 200° C. The scale corrections of the standard French thermometers of verre dur have been very carefully determined over the range 0° to 80° C. by P. Chappuis using a constant volume gas thermometer containing hydrogen (at an initial pressure of one metre of mercury at 0° C.) as the representative of the normal scale. His observations between 0° and 80° C. are represented by the quartic equation
| th−tm = (−61·859+0·47351 t−0·0011577 t 2)✕10−6, | (7) |
in which th and tm represent temperature on the scales of the hydrogen and mercury thermometers respectively. The verre dur mercury thermometer reads 0·112° C. above the hydrogen thermometer at 40° C. where the difference of the scales is a maximum. The scale corrections of the Jena-glass thermometers, deduced by comparison with the French verre dur, appear to be practically of the same magnitude, but show differences of as much as 0·010° C. on either side of the mean. It may be questioned whether it is possible to construct mercury thermometers with scales agreeing more closely than this, owing to inevitable variations in the quality and treatment of the glass. According to Guillaume, the scale of a French cristal thermometer tc differs from that of the standard verre dur tm between 0° and 50° C., according to the cubic formula
| tc−tm = t(100−t)(14·126−0·03511t)✕10−6, | (8) |
According to some unpublished observations made by the writer in 1893–1894, the scale of an English flint-glass thermometer, tested by comparison with a platinum thermometer, does not differ from that of the constant-pressure air thermometer by more than one or two hundredths of a degree between 0° and 100° C. But for the comparison of the scales to be of any value, it would be necessary to study a large number of such thermometers. It is possible to obtain much more consistent results if the thermometers are not heated above 50° C.
The comparisons of the verre dur thermometers with the normal scale at the International Bureau at Paris have not as yet extended beyond 100° C. The most important observations on the mercury thermometer above these limits appear to be those of Regnault. The later observations of J. M. Crafts were confined to French thermometers of cristal dur (Comptes Rendus, 1882, 95, p. 863). He found the following deviations from the hydrogen scale:—
| th | 150° | 170° | 200° | 230° | 250° | 280° | 300° | 330° |
| th−tm | +·25 | +·35 | +·27 | −·02 | −·26 | −·63 | −1·21 | −2·48 |
The correction changes sign at about 230° C., owing to the rapid increase in the expansion of mercury. Between 0° and 150° C. it would appear that the coefficient of expansion of glass increases more rapidly than that of mercury.
Poggendorff’s Correction.—It should be observed that, since in the construction of a mercury thermometer the tube is divided or calibrated so as to read in divisions of equal volume when the whole of the tube is at one temperature, the degrees do not as a matter of fact correspond to equal increments of the apparent expansion of mercury. The scale does not therefore agree in practice with the theoretical formula (1) for the scale of the expansion of mercury, since the expansion is measured in a tube which itself is expanding. A similar argument applies to the method of the weight thermometer, in which the overflow-is measured by weight. Even if the expansion of mercury and glass were both uniform, as measured on the thermodynamical scale, the scale of the mercury thermometer, as ordinarily calibrated, would not agree with the thermodynamical scale. The difference can be easily calculated if the actual expansion of mercury and glass is known. The correction is known as Poggendorff's, but is generally included in the scale correction, and is not applied separately. It has the effect of making the thermometer read higher at temperatures between 0° and 100° than it would if the divisions of the stem did not expand as the temperature rose. The amount of the correction for verre dur is given by Guillaume as
| P.C.=t(100−t)(23·920+0·0240t)✕10−6 | (9) |
The value of this correction is between ·060° and ·080° at 50° C. for different thermometers.
 |
| Fig. 2.—Differences between Scales of Mercury, and Gas Thermometers and Hydrogen Scale, according to Guillaume and Chappuis. |
Gas Thermometry
8. The deviations of the gas thermometer from the absolute scale are so small that this instrument is now universally regarded as the ultimate standard in thermometry. It had, in fact, already been adopted for this purpose by Regnault and others, on a priori considerations, before the absolute scale itself had been invented. Although the indications of a gas thermometer are not absolutely independent of the changes of volume of the envelope or bulb in which the gas is contained, the effect of any uncertainty in this respect is minimized by the relatively large expansibility of the gas. The capricious changes of volume of the bulb, which are so great a difficulty in mercurial thermometry, are twenty times less important in the case of the gas thermometer. As additional reasons for the choice we have the great simplicity of the laws of gases, and the approximate equality of expansion and close agreement of the thermometric scales of all gases, provided that they are above their critical temperatures. Subject to this condition, at moderate pressures and provided that they are not dissociated or decomposed, all gases satisfy approximately the laws of Boyle and Charles. These two laws are combined in the characteristic equation of the gaseous state, viz., pv=RT, in which p is the pressure and v the volume of unit mass of the gas in question, and R is a constant which varies inversely as the molecular weight of the gas, and is approximately equal to the difference of the specific heats.
9. Practical Conditions.—In practice it is not convenient to deal with unit mass, but with an arbitrary mass M occupying a space V, so that the specific volume v=V/M. It is also necessary to measure the pressure p in terms of mercury columns, and not in absolute units. The numerical value of the constant R is adjusted to suit these conditions, but is of no consequence in thermometry, as we are concerned with ratios and differences only. The equation may be written in the form T=pV/RM, but in order to satisfy the essential condition that T shall be a definite function of the temperature in the case of a gas which does not satisfy Boyle's law exactly, it is necessary to limit the application of the equation to special cases which lead to definite, but not necessarily identical, thermometric scales. There are three special cases of practical importance, corresponding to three essentially distinct experimental methods.
(i.) Volumetric Method (constant-pressure).—In this method V is variable and p and M are constant. This method was employed by Gay-Lussac, and is typified in the ideal thermometer with reservoir of variable capacity designed by Lord Kelvin (Ency. Brit., ed. ix., vol. xi. p. 575, fig. 10). It corresponds to the method ordinarily employed in the common liquid-in-glass thermometer, but is not satisfactory in practice, owing to the difficulty of making a bulb of variable and measurable volume the whole of which can be exposed to the temperature to be measured.
(ii.) Manometric Method (constant-volume or density).—In this method p is variable and V and M are constant. Variations of temperature are observed and measured by observing the corresponding variations of pressure with a mercury manometer, keeping a constant mass, M, of gas enclosed in a volume, V, which is constant except for the unavoidable but small expansion of the material of which the bulb is made.
(iii.) Gravimetric Method (constant-pressure).—In this method M is variable and p and V are constant. This method is generally confounded with (i.) under the name of the constant pressure method, but it really corresponds to the method of the weight thermometer, or the “overflow” method, and is quite distinct from an experimental standpoint, although it leads to the same thermometric scale. In applying this method, the weight M of the vapour itself may be measured, as in Regnault's mercury-vapour thermometer, or in Deville and Troost's iodine-vapour thermometer. The best method of measuring the overflow is that of weighing mercury displaced by the gas. The mass of the overflow may also be estimated by observing its volume in a graduated tube. but this method is much less accurate.
In addition to the above, there are mixed methods in which both p and V or M are variable, such as those employed by Rudberg or Becquerel; but these are unsatisfactory for precision, as not leading to a sufficiently definite thermometric scale. There is also a variation of the constant-volume method (ii.), in which the pressure is measured by the volumetric compression of an equal mass of gas kept at constant temperature, instead of by a manometer. This method is experimentally similar to (iii.), and gives the same equations, but a different thermometric scale from either (ii.) or (iii.). It will be considered with method (iii.), as the apparatus required is the same, and it is useful for testing the theory of the instrument. We shall consider in detail methods (ii.) and (iii.) only, as they are the most important for accurate work.
10. Construction of Apparatus.—The manometric or constant-volume method was selected by Regnault as the standard, and has been most generally adopted since his time. His apparatus has not been modified except in points of detail. A description of his instrument will be found in most text-books on heat. A simple and convenient form of the instrument for general use is Jolly's (described in Poggendorff's Jubelband, p. 82, 1874), and represented in fig. 3. The two vertical tubes of the manometer are connected by an india-rubber tube properly strengthened by a cotton covering, and they can be made to slide vertically up and down a wooden pillar which supports them; they are provided with clamps for fixing them in any position and a tangent screw for fine adjustment. The connexion between the bulb and the manometer is made by means of a three-way tap. The scale of the instrument is engraved on the back of a strip of plane mirror before silvering, and the divisions are carried sufficiently far across the scale for the reflections of the two surfaces of the mercury to be visible behind the, scale. Parallax can thus be avoided and an accurate reading obtained without the necessity of using a cathetometer. In order to allow for the expansion of the glass of the reservoir a weight-thermometer bulb is supplied with the instrument, made from another specimen of the same kind of glass, and the relative expansion of the mercury and the glass can thus be determined by the observer himself. The volume of the air-bulb and that of the capillary tube and the small portion of the manometer tube above the small beak of glass, the point of which serves as the fiducial mark, are determined by the
instrument makers. The improvements introduced by Chappuis, of the International Bereau at sèvres, in construction of the constant-volume hydrogen thermometer selected by the committee for the determination of the normal scale, are described in the text-books (e.g. Watson's Physics); The most important is the
 |
| Fig. 3. |
combination of the manometer and the barometer into a single instrument with a single scale, thus reducing the number of readings required. The level of the mercury in the branch of the manometer communicating with the bulb of the gas thermometer is adjusted in the usual manner up to a fixed contact-point, so as to reduce the contained gas to a constant volume. Simultaneously the barometer branch of the manometer is adjusted so that the surface of the mercury makes Contact with another point fixed in the upper end of the barometer tube. The distance between two contact-points, giving the pressure of the gas in the thermometer, is deduced from the reading of a vernier fixed relatively to the upper contact-point. This method of reading the pressure is probably more accurate than the method of the cathetometer which is usually employed, but has the disadvantage of requiring a double adjustment.
11. Pressure Correction.—In the practical application of the manometric method there are certain corrections peculiar to the method, of which account must be taken in work of precision. The volume of the bulb is not accurately constant, but varies with change of pressure and temperature. The thermal expansion of the bulb is common to all methods, and will be considered in detail later. The pressure correction is small, and is determined in the same manner as for a mercury thermometer. The value so determined, however, does not apply strictly except at the temperature to which it refers. If the pressure-coefficient were constant at all temperatures and equal to e, the pressure correction, dt, at any point t of the scale would be obtainable from the simple formula
| dt=ep₀t(t-100)/T₀ | (10) |
where p₀ is the initial pressure at the temperature T₀. But as the coefficient probably varies in an unknown manner, the correction is somewhat uncertain, especially at high temperatures. Another very necessary but somewhat troublesome correction is the reduction of the manometer readings to allow for the varying temperatures of the mercury and scale. Since it is generally impracticable to immerse the manometer in a liquid bath to secure certainty and uniformity of temperature, the temperature must be estimated from the readings of mercury thermometers suspended in mercury tubes or in the air near the manometer. It is therefore necessary to work in a room specially designed to secure great constancy of temperature, and to screen the manometer with the utmost care from the source of heat in measurements of high temperature. Regnault considered that the limit of accuracy of correction was one-tenth of a millimetre of mercury, but it is probably possible to measure to one-hundredth as a mean of several readings under the best conditions, at ordinary temperatures.
12. Stem-Exposure.—In all gas thermometers it is necessary in practice that the part of the gas in contact with the mercury or other liquid in the manometer should not be heated, but kept at a nearly constant temperature. The space above the mercury, together with the exposed portion of the capillary tube connecting the manometer with the thermometric bulb, may be called the “dead space.” If the volume of the dead space is kept as nearly as possible constant by adjusting the mercury always up to a fixed mark, the quantity of air in this space varies nearly in direct proportion to the pressure, i.e. in proportion to the temperature of the thermometric bulb at constant volume. This necessitates the application of a stem-exposure correction, the value of which is approximately given by the formula
| dt=rt(t−100)/T2, | (11) |
where r is the ratio of the volume of the dead space to the volume of the thermometric bulb, and T2 is the mean temperature of the dead space, which is supposed to be constant. The magnitude of the correction is proportional to the ratio r, and increases very rapidly at high temperatures. If the dead space is 1 per cent. of the bulb, the correction will amount to only one-tenth of a degree at 50° C., but reaches 5 ° at 445 °C., and 30° at 1000 °C. It is for this reason important in high-temperature work to keep the dead space as small as possible and to know its volume accurately. With a mercury manometer, the volume is liable to a slight uncertainty on account of changes of shape in the meniscus, as it is necessary to use a wide tube in order to secure accurate measurements of pressure.
 |
| Fig. 4.—Method of Compensation. |
13. Compensation Method with Oil-Gauge.—It is possible to avoid this difficulty, and to make the dead space very small, by employing oil or sulphuric acid or other non-volatile liquid to confine the gas in place of mercury (Phil. Trans., A. 1887, p. 171). The employment of a liquid which wets the tube makes it possible to use a much smaller bore, and also greatly facilitates the reading of small changes of pressure. At the same time the instrument may be arranged so that the dead space correction is automatically eliminated with much greater accuracy than it can be calculated. This is effected as shown diagrammatically in fig. 4, by placing side by side with the tube AB, connecting the bulb B to the manometer A, an exact duplicate CD, closed at the end D, and containing liquid in the limb C, which is of the same size as the branch A of the manometer and in direct communication with it. The tube CD, which is called the compensating tube, contains a constant mass of gas under exactly similar conditions of volume and temperature to the tube AB. If therefore the level of the liquid is always adjusted to be the same in both tubes AB and CD, the mass of gas contained in the dead space AB will also be constant, and is automatically eliminated from the equations, as they contain differences only.
14. Gravimetric Method.—In the writer's opinion, the gravimetric or overflow method, although it has seldom been adopted, and is not generally regarded as the most accurate, is much to be preferred to the manometric method, especially for work at high temperatures. It is free from the uncertain corrections above enumerated as being peculiar to the manometric method. The apparatus is much simpler to manipulate and less costly to construct. If the pressure is kept constant and equal to the external atmospheric pressure, there is no strain of the bulb, which is particularly important at high temperatures. There is no dead space correction so long as the temperature of the dead space is kept constant. The troublesome operation of reading and adjusting the mercury columns of the manometer is replaced by the simpler and more accurate operation of weighing the mercury displaced, which can be performed at leisure. The uncertain correction for the temperature of the mercury in the manometer is entirely avoided.
The reasons which led Regnault to prefer the constant-volume thermometer are frequently quoted, and are generally accepted as entirely conclusive, but it is very easy to construct the constant-pressure or gravimetric instrument in such a manner as to escape the objections which he urges against it. Briefly stated, his objections are as follows: (1) Any error in the observation of the temperature of the gas in the overflow space produces a considerable error in the temperature deduced, when the volume of the overflow is large. This source of error is very simply avoided by keeping the whole of the overflow in melting ice, an expedient which also considerably simplifies the equations. It happened that Regnault’s form of thermometer could not be treated in this manner, because he had to observe the level of the mercury in order to measure. the pressure and the volume. It is much better, however, to use a separate gauge, containing oil or sulphuric acid, for observing small changes of pressure. The use of ice also eliminates the correction for the variation of density of the mercury by which the overflow is measured. (2) Regnault's second objection was that an error in the measurement of the pressure, or in reading the barometer, was more serious at high temperatures in the case of the constant-pressure thermometer than in the constant-volume method. Owing to the incessant variations in the pressure of the atmosphere, and in the temperature of the mercury columns, he did not feel able to rely on the pressure readings (depending on observations of four mercury surfaces with the cathetometer) to less than a tenth of a millimetre of mercury, which experience showed to be about the limit of accuracy of his observations. This would be equivalent to an error of 0·036° with the constant-volume thermometer at any point of the scale, but with the constant-pressure thermometer the error would be larger at higher temperatures, since the pressure does not increase in proportion to the temperature. This objection is really unsound, because the ideal condition to be aimed at is to keep the proportionate error dT/T constant. That the proportionate error diminishes with rise of temperature, in the case of the constant-volume thermometer, is really of no advantage, because we can never hope to be able to measure high temperatures with greater proportionate accuracy than ordinary temperatures. The great increase of pressure at high temperatures in the manometric method is really a serious disadvantage, because it becomes necessary to work with much lower initial pressures, which implies inferior accuracy at ordinary temperatures and in the determination of the initial pressure and the fundamental interval.
15. Compensated Differential Gas Thermometer.—The chief advantage of the gravimetric method, which Regnault and others appear to have missed, is that it is possible to make the measurements altogether independent of the atmospheric pressure and of the observation of mercury columns. This is accomplished by using, as a standard of constant pressure, a bulb S, fig. 5, containing a constant mass of gas in melting ice, side by side with the bulb M, in which the volume of the overflow is measured. The pressure in the thermometric bulb T is adjusted to equality with the standard by means of a delicate oil-gauge G of small bore, in which the difference of pressure is observed by means of a cathetometer microscope. This kind of gauge permits the rapid observation of small changes of pressure, and is far more accurate and delicate than the mercury manometer. The fundamental measurement of the volume of the overflow in terms of the weight of mercury displaced at 0°C. involves a single weighing made at leisure, and requires no temperature correction. The accuracy obtainable at ordinary temperatures in this measurement is about ten times as great as that attainable under the best conditions with the mercury manometer. At higher temperatures the relative accuracy diminishes in proportion to the absolute temperature, or the error dt increases according to the formula
| dt/t =− (T/T0) dw/w, | (12) |
where w is the weight of the overflow and dw the error. This diminution of the sensitiveness of the method at high temperatures is commonly urged as a serious objection to the method, but the objection is really without weight in practice, as the possible accuracy of measurement is' limited by other conditions. So far as the weighing alone is concerned, the method is sensitive to one-hundredth of a degree at 1000°C., which is far beyond the order of accuracy attainable in the application of the other corrections.
16. Method of Using the Instrument.—A form of gas thermometer constructed' on the principles above laid down, with the addition of a duplicate set of connecting tubes C for the elimination of the stem-exposure correction by the method of automatic compensation already explained, is shown in fig. 5 (Proc. R. S. vol. 50, p. 243; Preston's Heat, p. 133).
In setting up the instrument, after cleaning, and drying and calibrating the bulbs and connecting tubes, the masses of gas on the two sides are adjusted as nearly as possible to equality, in order that any changes of temperature in the two sets of connecting tubes may compensate each other. This is effected with all the bulbs in melting ice, by adjusting the quantities of mercury in the bulbs M and S and equalizing the pressures. The bulb T is then heated in steam to determine the fundamental interval. A weight w1 of mercury is removed from the overflow bulb M in order to equalize the pressures again. If W is the weight of the mercury at 0°C which would be required to fill the bulb T at 0°C., and if W+dW1 is the weight of mercury at 0° which would be required to fill a volume equal to that of the bulb in steam at t1, we have the following equation for determining the coefficient of expansion a, or the fundamental zero Tₒ,
| at1=t1/T0=(w1+dW1)/(W−w1), | (13) |
Similarly if w is the overfiow when the bulb is at any other temperature t, and the expansion of the bulb is dW, we have a precisely similar equation for determining t in terms of T0, but with t and w and dW substituted for t1 and w1 and d/W1. In practice, if the pressures are not adjusted to exact equality, or if the volumes of
| |
| Fig. 5.—Compensated Differential Gas Thermometer. |
the connecting tubes do not exactly compensate, it is only necessary to include in w a small correction dw, equivalent to the observed difference, which need never exceed one part in ten thousand.
It is possible to employ the same apparatus at constant volume as well as at constant pressure, but the manipulation is not quite so simple, in consequence of the change of pressure. Instead of removing mercury from the overflow bulb M in Connexion with the thermometric bulb, mercury is introduced from a higher level into the standard bulb S so as to raise its pressure to equality with that of T at constant volume. The equations of this method are precisely the same as those already given, except that; w now signifies the* “inflow” weight introduced into the bulb S, instead of the overflow weight from M. It is necessary, however, to take account of the pressure-coefficient of the bulb T, and it is much more important to have the masses of gas on the two sides of the apparatus equal than in the other case. The thermometric scale obtained in this method differs slightly from the scale of the manometric method, on account of the deviation of the gas compressed at o°C. from Boyle's law, but it is easy to take account of this with certainty.
Another use to which the same apparatus may be put is the accurate comparison of the scales of two different gases at constant volume by a differential method. It is usual to effect this comparison indirectly, by comparing the gas thermometers separately with a mercury thermometer, or other secondary standard. But by using a pair of bulbs like M and S simultaneously in the same bath, and measuring the small difference of pressure with an oilgauge, a higher order of accuracy may be attained in the measurement of the small differences than by the method of indirect comparison. For instance, in the curves representing the difference between the nitrogen and hydrogen scales (fig. 1), as found by Chappuis by comparison of the nitrogen and hydrogen thermometers with the mercury thermometer, it is probable that the contrary flexure of the curve between 70° and 100° C. is due to a minute error of observation, which is quite as likely to be caused by the increasing aberrations of the mercury thermometer at these temperatures as by the difficulties of the manometric method. It may be taken as an axiom in all such cases that it is better to measure the small difference itself directly than to deduce it from the much more laborious observations of the separate magnitudes concerned.
17. Expansion Correction.—In the use of the mercury thermometer we are content to overlook the modification of the scale due to the expansion of the envelope, which is known as Poggendorff's correction, or rather to include it in the scale correction. In the case of the gas thermometer it is necessary to determine the expansion correction separately, as our object is to arrive at the closest approximation possible to the absolute scale. It is a common mistake to imagine that if the rate of expansion' of the bulb were uniform, the scale of the apparent expansion of the gas would be the same as the scale of the real expansion—in other words, that the correction for the expansion of the bulb would affect the value of the coefficient of expansion 1/T0 only, and would be without effect on the value of the temperature t deduced. A result of this kind would be produced by a constant error in the initial pressure on the manometric method, or by a constant error in the initial volume on the volumetric method, or by a constant error in the fundamental interval on any method, but not by a constant error in the coefficient of expansion of the bulb, which would produce a modification of the scale exactly analogous to Poggendorff’s, correction. The correction to be applied to the value of t in any case to allow for any systematic error or variation in the data is easily found by differentiating the formula for t with respect to the variable considered. Another method, which is in some respects more instructive, is the following:—
Let T be the function of the temperature which is taken as the basis of the scale considered, then we have the value of t given by the general formula (1), already quoted in § 3. Let dT be the correction to be added to the observed value of T to allow for any systematic change or error in the measurement of any of the data on which the value of T depends, and let dt be the corresponding correction produced in the value of t, then substituting in formula (1) we have,
| t+dt=100(T−Tₒ+dT−dTₒ)/(T1−Tₒ+dT1−dT0), |
from which, provided that the variations considered are small, we obtain the following general expression for the correction to t,
| dt=(dT −dTₒ) − (dT1 − dT0)t/ 100. | (14) |
It is frequently simpler to estimate the correction in this manner, rather than by differentiating the general formula.
In the special case of the gas thermometer the value of T is given by the formula
| T=pV/RM=pV/R(M0−M2), | (15) |
where p is the observed pressure at any temperature t, V the volume of the thermometric bulb, and M the mass of gas remaining in the bulb. The quantity M cannot be directly observed, but is deduced by subtracting from the whole mass of gas M0 contained in the apparatus the mass M2 which is contained in the dead space and overflow bulb. In applying these formulae to deduce the effect of the expansion of the bulb, we observe that if dV is the expansion from 0°C., and V0, the volume at 0°C., we may write
| V=Vₒ+dV, T=p(Vₒ+dV)/RM=(pV0/RM)(1+dV/V0), |
whence we obtain approximately
| dT=TdV/Vₒ | (16) |
If the coefficient of expansion of the bulb is constant and equal to the fundamental coefficient f (the mean coefficient between 0° and 100° C.), we have simply dV/V0=ft; and if we substitute this value in the general expression (14) for dt, we obtain
| dt=(T−T1)ft=ft(t−100) | (17) |
Provided that the correction can be expressed as a rational integral function of t, it is evident that it must contain the factor stand (t−100), since by hypothesis the scale must be correct at the fixed points 0° and 100°C., and the correction must vanish at these points. It is clear from the above that the scale of the gas thermometer is not independent of the expansion of the bulb even in the simple case where the coefficient is constant. The correction is by no means unimportant. In the case of an average glass or platinum reservoir, for which f may be taken as 0·000025 nearly, the correction amounts to −0·0625° at 50° C., to 3·83° at 445° C., and to 22·5° at 1000° C.
The value of the fundamental coefficient f can be determined with much greater accuracy than the coefficient over any other range of temperature. The most satisfactory method is to use the bulb itself as a mercury weight thermometer, and deduce the cubical expansion of the glass from the absolute expansion of mercury as determined by Regnault. Unfortunately the reductions of Regnault’s observations by different calculators differ considerably even for the fundamental interval. The values of the fundamental coefficient range from ·00018153 Regnault, and ·00018210 Broch, to ·00018253 Wüllner. The extreme difference represents an uncertainty of about 4 per cent. (1 in 25) in the expansion of the glass. This uncertainty is about 100 times as great as the probable error of the weight thermometer observations. But the expansion is even less certain beyond the limits of the fundamental interval. Another method of determining the expansion of the bulb is to observe the linear expansion of a tube or rod of the same material, and deduce the cubical expansion on the assumption that the expansion is isotropic. It is probable that the uncertainty involved in this assumption is greater in the case of glass or porcelain bulbs, on account of the difficulty of perfect annealing, than in the case of metallic bulbs.
Except for small ranges of temperature, the assumption of a constant coefficient of expansion is not sufficiently exact. It is therefore usual to assume that the coefficient is a linear function of the temperature, so that the whole expansion from 0° C. may be expressed in the form d V=t(a+bt)V0, in which case the fundamental coefficient f=a+100b. Making this substitution in the formula already given, we obtain the whole correction
| dt=(f+bT)t(t−100) | (18) |
It will be observed that the term involving b becomes of considerable importance at high temperatures. Unfortunately, it cannot be determined with the same accuracy as f, because the conditions of observation at the fixed points are much more perfect than at other temperatures. Provided that the range of the observations for the determination of the expansion is co-extensive with the range of the temperature measurements for which the correction is required, the uncertainty of the correction will not greatly exceed that of the expansion observed at any point of the range. It is not unusual, however, to deduce the values of b and f from observations confined to the range 0° to 100° C., in which case an error of 1 per cent., in the observed expansion at 50° C., would mean an error of 60 per cent. at 445°, or of 360 per cent. at 1000° C. (Callendar, Phil. Mag. December 1899). Moreover, it by no means follows that the average value of b between 0° and 100° C. should be the same as at higher or lower temperatures. The method of extrapolation would therefore probably lead to erroneous results in many cases, even if the value could be determined with absolute precision over the fundamental interval. It is probable that this expansion correction, which cannot be reduced or eliminated like many of the other corrections which have been mentioned, is the chief source of uncertainty in the realization of the absolute scale of temperature at the present time. The uncertainty is of the order of one part in five or ten thousand on the fundamental interval, but may reach 0·5° at 500° C., and 2° or 3° at 1000° C.
18. Thermodynamical Correction.—Of greater theoretical interest, but of less practical importance on account of its smallness, is the reduction of the scale of the gas thermometer to the thermodynamical scale. The deviations of a gas from the ideal equation pv=Rθ may be tested by a variety of different methods, which should be employed in combination to determine the form of the characteristic equation. The principal methods by which the problem has been attacked are the following:—
(1) By the comparison of gas thermometers filled with different gases or with the same gas at different pressures (employing both gravimetric and manometric methods) the differences in their indications are observed through as wide a range of temperature as possible. Regnault, employing this method, found that the differences in the scales of the permanent gases were so small as to be beyond the limits of accuracy of his observations. Applying greater refinements of measurement, Chappuis and others have succeeded in measuring small differences, which have an important bearing on the type of the characteristic equation. They show, for instance, that the equation of van der Waals, according to which all manometric gas thermometers should agree exactly in their indications, requires modification to enable it to represent the behaviour of gases even at moderate pressures.
(2) By measuring the pressure and expansion coefficients of different gases between 0° and 100° C. the values of the fundamental zero (the reciprocal of the coefficient of expansion or pressure) for each gas under different conditions may be observed and compared. The evidence goes to show that the values of the fundamental zero for all gases tend to the same limit, namely, the absolute zero, when the pressures are indefinitely reduced. The type of characteristic equation adopted must be capable of representing the variations of these coefficients.
(3) By observing the variations of the product pv with pressure at constant temperature the deviations of different gases from Boyle’s law are determined. Experiment shows that the rate of change of the product pv with increase of pressure, namely d(pv)/dp, is very nearly constant for moderate pressures such as those employed in gas thermometry. This implies that the characteristic equation must be of the type
| v=F(θ)/P+f(θ) | (19) |
in which F(θ) and f(θ) are functions of the temperature only to a first approximation at moderate pressures. The function F(θ), representing the limiting value of pv at zero pressure, appears to be simply proportional to the absolute temperature for all gases. The function f(θ), representing the defect of volume from the ideal volume, is the slope of the tangent at p=0 to the isothermal of θ on the pv,p diagram, and is sometimes called the “angular coefficient.” It appears to be of the form b−c, in which b is a small constant quantity, the “co-volume,” of the same order of magnitude as the volume of the liquid, and c depends on the cohesion or co-aggregation of the molecules, and diminishes for all gases continuously and indefinitely with rise of temperature. This method of investigation has been very widely adopted, especially at high pressures, but is open to the objection that the quantity b−c is a very small fraction of the ideal volume in the case of the permanent gases at moderate pressures, and its limiting value at p=0 is therefore difficult to determine accurately.
(4) By observing the cooling effect dθ/dp, or the ratio of the fall of temperature to the fall of pressure under conditions of constant total heat, when a gas flows steadily through a porous plug, it is possible to determine the variation of the total heat with pressure from the relation
| Sdθ/dp=θdv/dθ−v | (20) |
(See Thermodynamics, § 10, equation 15.) This method has the advantage of directly measuring the deviations from the ideal state, since θdv/dθ=v for an ideal gas, and the cooling effect vanishes. But the method is difficult to carry out, and has seldom been applied. Taken in conjunction with method (3), the observation of the cooling effect at different temperatures affords most valuable evidence with regard to the variation of the defect of volume c−b from the ideal state. The formula assumed to represent the variations of c with temperature must be such as to satisfy both the observations on the compressibility and those on the cooling effect. It is possible, for instance, to choose the constants in van der Waals’s formula to satisfy either (3) or (4) separately within the limits of experimental error, but they cannot be chosen so as to satisfy both. The simplest assumption to make with regard to c is that it varies inversely as some power n of the absolute temperature, or that c = c0(θ0/θ)n, where c0 is the value of c at the temperature θ0. In this case the expression θdv/dθ−v takes the simple form (n+1)c−b. The values of n, c and b could be calculated from observations of the cooling effect Sdθ/dp alone over a sufficient range of temperature, but, owing to the margin of experimental error and the paucity of observations available, it is better to make use of the observations on the compressibility in addition to those on the cooling effect. It is preferable to calculate the values of c and b directly from equation (20), in place of attempting to integrate the equation according to Kelvin’s method (Ency. Brit. ed. ix. vol. xi. p. 573), because it is then easy to take account of the variation of the specific heat S, which is sometimes important.
Calculation of the Correction.—Having found the most probable values of the quantities c, b and n, from the experimental data, the calculation of the correction may be very simply effected as follows: The temperature by gas thermometer is defined by the relation T=pv/R, where the constant R is determined from the observations at 0° and 100° C. The characteristic equation in terms of absolute temperature θ may be put in the form θ=pv/R′+q, where q is a small quantity of the same dimensions as temperature, given by the relation
| q=(c−b)p/R | (21) |
The constant R′ is determined, as before, by reference to the fundamental interval, which gives the relation R′/R=1+(q1−q0)/100, where q1 and q0 are the values of q at 100° and 0° C. respectively.
The correction to be added to the fundamental zero T0 of the gas thermometer in order to deduce the value of the absolute zero θ0 (the absolute temperature corresponding to 0° C.) is given by the equation,
| θ0−T0=q0−(q1−q0)θ0/100 | (22) |
The correction dt to be added to the centigrade temperature t by gas thermometer reckoned from 0° C. in order to deduce the corresponding value of the absolute temperature also reckoned from 0° C. is given by the relation, deduced from formula (14),
| dt=(q−q0)−(q1−q0)t/100 | (23) |
where q is the value at t ° C. of the deviation (c−b)p/R. The formulae may be further simplified if the index n is a simple integer such as 1 or 2. The values of the corrections for any given gas at different initial pressures are directly proportional to the pressure. Values of the Corrections.—If we take for the gas hydrogen the values c=1·5 c.c. at 0° C., b=8·0 c.c., with the index n=1·5, which satisfy the observations of Joule and Thomson on the cooling effect, and those of Regnault, Amagat and Chappuis on the compressibility, the values of the absolute zero θ0, calculated from Chappuis’s values of the pressure and expansion coefficients at 100 cms. initial pressure, are found to be 273·10° and 273·05° respectively, the reciprocals of the coefficients themselves being 273·03 and 273·22. The corrections are small and of opposite signs. For nitrogen, taking c0=1·58, b=1·14, n=1·5, we find similarly 273·10° and 273·13° for the absolute zero, the correction θ0–T0 in this case amounting to nearly 1°. The agreement is very good consider in the difficulty of determining the small deviations c and b, and the possible errors of the expansion and pressure-coefficients. It appears certain that the value of the absolute zero is within a few hundredths of a degree of 273·10°. Other observations confirm this result within the limits of experimental error. The value of the index n has generally been taken as equal to 2 for diatomic gases, but this does not satisfy either the observations on the cooling effect or those on the compressibility so well as n=1·5, although it makes comparatively little difference to the value of the absolute zero. The value deduced from Travers’s observation of the pressure-coefficient of helium is 273·13°, taking n=12, which is the probable value of the index for a monatomic gas. The application of the method to the condensible gas carbonic acid is interesting as a test of the method (although the gas itself is not suited for thermometry), because its deviations from the ideal state are so large and have been so carefully studied. The observations of Joule and Thomson on the cooling effect give c0=3·76 c.c., b=0·58 c.c., n=2, provided that allowance is made for the variation of the specific heat with temperature as determined by Regnault and Wiedemann. Chappuis’s values of the pressure and expansion coefficients agree in giving 273·05° for the absolute zero, the values of the corrections θ0–T0 being 4·6° and 5·8° respectively.
The values of the scale correction dt deduced from these formulae agree with those experimentally determined by Chappuis in the case of carbonic acid within the limits of agreement of the observations themselves. The calculated values for nitrogen and hydrogen give rather smaller differences than those found experimentally, but the differences themselves are of the same order as the experimental errors. The deviations of hydrogen and helium from the absolute scale between 0° and 100° C. are of the order of ·001° only, and beyond the limits of accuracy of experiment. Even at −250° C. (near the boiling-point of hydrogen) the corrections of the constant volume hydrogen and helium thermometers are only a tenth of a degree, but, as they are of opposite signs, the difference amounts to one-fifth of a degree at this point, which agrees approximately with that observed by Travers. For a fuller discussion of the subject, together with tables of corrections, the reader may refer to papers by Callendar, Phil. Mag. v. p. 48 (1903). and D. Berthelot, Trav. et Mém. Bur. Int. Paris, xiii. (1903). Berthelot assumes a similar type of equation to that given above, but takes n=2 in all cases, following the so-called law of corresponding states. This assumption is of doubtful validity, and might give rise to relatively large errors in the case of monatornic gases.
19. Limitations.—In the application of the gas thermometer to the measurement of high temperatures certain difficulties are encountered which materially limit the range of measurement and the degree of accuracy attainable. These may be roughly classified under the heads—(1) changes in the volume of the bulb; (2) leakage, occlusion and porosity; (3) chemical Change and dissociation. The difficulties arise partly from defects in the materials available for the bulb, and partly from the small mass of gas enclosed. The troubles due to irregular changes of volume of glass bulbs, which affect the mercury thermometer at ordinary temperatures, become so exaggerated at higher points of the scale as to be a serious source of trouble in gas thermometry in spite of the twenty fold larger expansion. For instance, the volume of a glass bulb will be diminished by from one-quarter to one-half of 1 per cent. the first time it is heated to the temperature of boiling sulphur (445° C.). This would not matter so much if the volume then remained constant. Unfortunately, the volume continues to change, especially in the case of hard glass, each time it is heated, by amounts which cannot be predicted, and which are too large to neglect. The most accurate method of taking account of these variations in a series of observations, without recalibrating and refilling and cleaning the bulb, is to assume the known constant value of the coefficient of expansion of the gas, and to calculate the volume of the bulb at any time by taking observations in icei and steam (Phil. Trans. A. 1891, vol. 182, p. 124). Similar changes take place with porcelain at higher temperatures. Metallic bulbs are far more perfect than glass bulbs in this respect. It is probable that silica bulbs would be the most perfect. The writer suggested the use of this material (in the Journ. Iron and Steel Inst. for 1892), but failed to construct bulbs of sufficient size. W. A. Shenstone, however, subsequently succeeded, and there seems to be a good prospect that this difficulty will soon be minimized. The difficulties of leakage and porosity occur chiefly with porcelain bulbs, especially if they are not perfectly glazed inside. A similar difficulty occurs with metallic bulbs of platinum or platinum-iridium, in the case of hydrogen, which passes freely through the metal by occlusion at high temperatures. The difficulty can be avoided by substituting either nitrogen or preferably argon or helium as the thermometric material at high temperatures. With many kinds of glass and porcelain the chemical action of hydrogen begins to be appreciable at temperatures as low as 200° or 300° C. In any case, if metallic bulbs are used, it is absolutely necessary to protect them from furnace gases which may contain hydrogen. This can be effected either by enclosing the bulb in a tube of porcelain, or by using some method of electric heating which cannot give rise to the presence of hydrogen. At very high temperatures it is probable that the dissociation of diatomic gases like nitrogen might begin to be appreciable before the limit of resistance of the bulb itself was reached. It would probably be better, for this reason, to use the monatomic and extremely inert gases argon or helium.
20. Other Methods.—Many attempts have been made to overcome the difficulties of gas pyrometry by adopting other methods of measurement. Among the most interesting may be mentioned: (i.) The variation in the wave-length of sound. The objection to this method is the difficulty of accurately observing the wave-length, and of correcting for the expansion of the material of the tubes in which it is measured. There is the further objection that the velocity varies as the square root of the absolute temperature. (ii.) A similar method, but more promising, is the variation of the refractivity of a gas, which can be measured with great accuracy by an interference method. Here again there is difficulty in determining the exact length of the heated column of gas, and in maintaining the temperature uniform throughout a. long column at high temperatures. These difficulties have been ingeniously met by D. Berthelot (Comptes Rendus, 1895, 120, p. 831). But the method is not easy to apply, and the degree of accuracy attainable is probably inferior to the bulb methods. (iii.) Methods depending on the effusion and transpiration of gases through fine orifices and tubes have been put in practice by Barus and by the writer. The method of transpiration, when the resistance of the tube through which the current of gas is passed is measured on the Wheatstone bridge principle (Nature, 23rd March 1899), is extremely delicate, and the apparatus may be made very small and sensitive, but the method cannot be used for extrapolation at high temperatures until the law of increase of resistance has been determined with certainty. This may be successfully accomplished in the near future, but the law is apparently not so simple as is usually supposed.
On account of these and similar difficulties, the limit of gas thermometry at the present time must be placed at 1500° C., or even lower, and the accuracy with which temperatures near 1000° C. are known does not probably exceed 2° C. Although measurements can be effected with greater consistency than this by means of. electrical pyrometers, the absolute values corresponding to those temperatures must remain uncertain to this extent, inasmuch as they depend on observations made with the gas thermometer.
Electrical Thermometry
21. The convenience of the mercurial thermometer lies in the fact that it is complete in itself, and can be read without subsidiary appliances beyond a magnifying glass. Its weakness lies in the very limited range of each single instrument, and in the troublesome and often uncertain corrections which must be applied to its readings in all work of precision. Electrical thermometers have the disadvantage of requiring auxiliary apparatus, such as galvanometers and resistances, the use of which involves some electrical training. But they far surpass the mercurial thermometer in point of range, delicacy and adaptability, and can be applied to many investigations in which ordinary thermometers are quite useless.
There are two kinds of electrical thermometers, which depend on different effects of heat on the electrical properties of metals: (1) The Thermocouple, or Thermopile, which depends on the production of a thermoelectric force when the junctions of different metals in an electric circuit are at different temperatures; and (2) the Electrical Resistance Thermometer, the action of which depends on the fact that the resistance of a pure metal to the passage of an electric current increases very considerably when the temperature is raised. The theory of the thermocouple is discussed in the article Thermoelectricity, as it possesses many points of interest, and has been studied by many skilful experimentalists. The electrical resistance thermometer is of more recent origin; but although the theory has been less fully developed, the practice of the method bids fair to surpass all others in the variety and accuracy of its applications. In order to secure the widest possible range and the greatest constancy, in either variety of electrical thermometer, advantage is taken of the great stability and in fusibility characteristic of the metals of the platinum group. Other metals are occasionally used in work at low temperatures with thermocouples for the sake of obtaining a larger electromotive force, but the substitution is attended with loss of constancy and uncertainty of reduction, unless the range is greatly restricted.
22. Applicatians of the Thermocouple.—The principal uses of the thermocouple in thermometry are for measuring high temperatures, and for measuring small differences of temperature, more particularly when the temperature is required to be measured at a point, or in a very small space. The electromotive force of the couple depends only on the temperature at the plane of junction of the two metals, which can be very exactly located. A typical instance of a measurement to which the thermocouple is peculiarly suited, is the determination' of the cyclical variations of temperature at accurately measured depths from one-tenth to one-hundredth of an inch in the metal of the cylinder of a heat engine, the interior surface of which is exposed to cyclical variations of temperature in the working of the engine.[1] The exact depth of the plane of junction can be measured without difficulty to the thousandth of an inch. The insertion of the wire makes the least possible disturbance of the continuity of the metal. There is no lag, as the thermometer itself is part of the metal. The instantaneous value of the temperature at any particular 'point of the stroke can be measured separately by setting a periodic contact to close the circuit of the galvanometer at the desired point. A further advantage is gained by measuring only the difference of temperature between two junctions of a thermocouple at different depths, instead of the whole interval from some fixed point. None of these advantages could be secured by the use of any ordinary thermometer; some depend on the fact that the method is electrical, but some are peculiar to the thermocouple, and could not be otherwise attained.
On the other hand, the thermocouple is not Well suited for thermometry of precision on account of the smallness of the electromotive force, which is of the order of ten micro volts only per degree for the most constant couples. By the use of very delicate galvanometers it is possible to read to the hundredth or even in special cases to the thousandth of a degree on this small difference, but unfortunately it is not possible to eliminate accidental thermal effects in other parts of the circuit due to small differences of temperature and material. These accidental effects seldom amount to less than one or two micro volts even in the best work, and limit the accuracy attainable in temperature measurement to about the tenth of a degree with a single platinum thermocouple. This limit can be surpassed by using couples of greater thermoelectric power and less permanence, or by using a pile or series of couples, but in either case it is doubtful whether the advantage gained in power is not balanced by loss of simplicity and constancy. A method of avoiding these effects, which the writer has found to be of great use in delicate thermoelectric researches, is to make the whole circuit, including all the terminals and even the slide wire itself, of pure copper. Platinoid, german silver, constantan and other alloys most commonly used for resistances and slide wires, are particularly to be avoided, on account of their great thermoelectric power when connected to copper. Manganin and platinum-silver are the least objectionable, but the improvement effected by substituting copper is very marked. It is clear that this objection to the use of the couple does not apply so strongly to high temperatures, because the electromotive force of the couple itself is greater, and the accuracy attainable is limited by other considerations.
23. The Resistance Thermometer.—In practice the resistance thermometer is almost invariably made of platinum, since there is very seldom any advantage to be gained by the substitution of baser metals. The instrument is for this reason often referred to simply as the “platinum thermometer.” It is important that the platinum should be pure, both for the sake of uniformity and also because the change of electrical resistance with temperature is greatly diminished by impurities. The observation of the fundamental coefficient, which is .00390 (or rather larger than the coefficient of expansion of a gas) for the purest metal hitherto obtained, is one of the most delicate tests of the purity of the metal. In addition to the constancy and in fusibility of the metal, a special advantage which is secured by the use of platinum is the close agreement of the thermodynamical scale with the platinum scale of temperature, as defined by the formula
| pt = 1001(R-R₀)/(R₁-R₀), | (24) |
in which the symbol pt stands for the temperature on the platinum scale centigrade, and R, R₁ and R₀ are the observed resistances of the thermometer at the temperatures pt, 100° and 0°C. respectively. A platinum thermometer is generally arranged to read directly in degrees of temperature on the platinum scale, just as a mercury thermometer is graduated in degrees of the mercury scale. The reduction to the scale 'of the gas thermometer is most conveniently effected by the difference formula
| t-pt=dt(t-100)/10,000, | (25) |
in which d is a constant, called the difference-coefficient, the value of which for pure platinum is about 1.50, but varies slightly for different specimens. This formula was first given by the writer as the result of a series of comparisons of different platinum wires with each other and with other metals, and also with an air thermometer over the range 0° to 625°C. The platinum wire in these comparisons was enclosed inside the bulb of the air thermometer itself, and disposed in such a manner as to be at the mean temperature of the bulb in case the temperature was not quite uniform throughout (Phil. Trans. A. 1887, p. 161). The formula was subsequently verified by C. T. Heycock and F. H. Neville (Journ. Chem. Soc. February 1895), by the observation of a number of higher points up to the freezing-point of copper at 1082°C., which they showed to agree with the most probable mean of all the best determinations by various methods of gas thermometry. At still higher temperatures, beyond the present range of the gas thermometer, the writer has succeeded in obtaining presumptive evidence of the validity of the same formula by comparison with the scales of the expansion and the specific heat of platinum, which appear to follow similar laws (Phil. Mag. December 1899). If we assume that the coefficient of expansion of platinum, the coefficient of increase of resistance, and the specific heat are all three linear functions of the temperature, we obtain results which are in agreement within the limits of error of observation up to the fusing-point of platinum itself. The same formula has been independently verified by the comparison of platinum thermometers with the constant volume nitrogen thermometer by Harker and Chappuis (Phil. Trans. A. 1900), working at the International Bureau at Sevres, over the range 0° to 650° C. It has also been shown to satisfy very closely the observations on the variation of electrical resistance of other metals over wide ranges of, temperature. Although the theoretical explanation of the formula has not yet been given, owing to our ignorance of the true nature of electrical conduction and of the molecular constitution of metals, it may be regarded from an empirical point of view as being one of the most accurately established of all thermometric formulae. It will be observed that it also represents the simplest possible type of divergence from the thermodynamical scale.
24. Methods and Apparatus.—The methods of electrical thermometry may be roughly classified under two heads as (r) deflection methods, in which the temperature is deduced from the observed deflection of a galvanometer; and (2) balance methods, in which the resistance or the electromotive force is balanced against a known adjustable resistance or potential difference. The former methods are most suitable for rough work and rapid reading, the latter for 'accurate measurements. In the practice of the deflection method it is customary to use a. movable-coil galvanometer, the sensitiveness of which can be varied by varying the resistance in circuit, or by varying the stiffness of the suspension. The accuracy attainable is of the order of one-half of 1 per cent. on the deflection, and is limited by variations of resistance of the galvanometer, and by the imperfect elasticity of the suspension. In any case the scale of the galvanometer should be calibrated or tested for uniformity. In this kind of work the thermocouple has the advantage over the resistance thermometer in that the latter requires an auxiliary battery to supply the current; but in many cases this is no disadvantage, because it permits a greater latitude of adjustment, and makes it possible to obtain greater power than with the thermocouple.
In cases where it is desired to obtain greater accuracy Without abandoning the quickness of reading which is the principal advantage of the deflection method, it is possible to combine the two methods by balancing part of the potential difference by means of a potentiometer and using the galvanometer for the small changes only. In cases where the greatest accuracy is required, a very sensitive galvanometer should be used, and the whole of the potential difference should be balanced as nearly as possible, leaving very little to depend on the deflection of the galvanometer. The degree of sensitiveness and accuracy obtainable depends primarily on the delicacy of the galvanometer, on the power available, and on the steadiness of the conditions of experiment. For thermometry of precision the resistance thermometer possesses three very great advantages over the thermocouple: (1) The power available, owing to the use of a battery, is much greater; (2) it is possible completely to eliminate the errors due to accidental thermal effects by reversing the battery; (3) the Wheatstone bridge method can be employed in place of the potentiometer, so that the constancy of the battery is immaterial, and it is not necessary to use a standard cell. The conditions to be satisfied in the attainment of the greatest possible accuracy in the measurement of temperature by this method differ somewhat from those which obtain in ordinary measurements of resistance, so that a special type of apparatus has been evolved for the purpose, a brief description of which will be given.
25. Compensated Bridge Apparatus.—It is necessary that the thermometer should be connected to the measuring apparatus by wires or “leads” of considerable length, generally at least two or three metres, in order to avoid exposing the galvanometer and resistance box, or other delicate parts of tire apparatus, to changes of temperature. It is also essential that the leads should not be too thick or heavy, for convenience in handling and to prevent conduction of heat along the stem of the thermometer. The resistance of that part of the leads. which is exposed to variations of temperature necessarily changes, and would give rise to serious errors if it were not determined or compensated. 'The method now generally adopted in accurate work is to compensate the variations of resistance of the leads by an exactly similar pair of dummy leads called the “compensator” and connected as shown diagrammatically in fig. 6. The battery, consisting of a single cell, with a rheostat and reversing key in circuit, is connected to the terminals AB of the two equal resistance coils AG, GB, which form the ratio arms of the balance. These coils must be carefully tested for equality of temperature-coefficient, and placed in close proximity to each other so as to be always at the same temperature. If they are inter wound on the same reel, they must be most carefully insulated from each other. In parallel circuit with the ratio coils are connected the compensator CC' and the balancing resistances C′E, on one side of the bridge-wire EF, and the compensating resistances FP and the pyrometer and leads PRP′ on the other side. The galvanometer is connected to the point G between the ratio coils, and to the sliding contact D on the bridge-wire. Since the ratio coils are always equal, equal changes of resistance on either side of D are eliminated, and do not affect the balance. Thus the changes of the pyrometer leads PP′ are balanced by the equal changes of the compensator leads CC′ on the other side. As a further refinement, which is of some importance in delicate work, the ends of the compensator leads are connected by a short piece of the same wire as the pyrometer coil. For instance, in observing the variations of temperature of the steam in the cylinder of a steam engine at different points of the stroke with a very delicate thermometer made of wire one-thousandth of an inch in diameter (Proc. Inst. C. E., vol. cxxxi. fig. 16, p. 23), the ends of the fine wire attached to the thick leads could not follow the rapid variations of temperature, and it was found necessary to adopt this device to eliminate the end-effect. It is also useful in other cases to eliminate the effect of conduction along the leads in cooling the ends of the fine wire coil. The balancing resistances C′E are made of some alloy such as manganin or platinum-silver, the resistance
An image should appear at this position in the text. If you are able to provide it, see Wikisource:Image guidelines and Help:Adding images for guidance. |
Fig. 6.—Diagram of Compensated Bridge Method.
of which varies very little with change of temperature. Platinum-silver is probably the best material, as it can be perfectly annealed at a red heat without risk of burning, and is then extremely constant. Unless the box can be kept at an absolutely constant and uniform temperature, which is not impossible but often inconvenient, it is necessary to allow for the change of resistance of the balancing coils C′E due to change in the temperature of the box. The temperature of the coils cannot be accurately determined with a mercury thermometer unless they are immersed in oil, but even in that case it is necessary to know the temperature-coefficient of each individual coil. A more convenient and accurate method, which eliminates the correction automatically, is to compensate each individual coil of the balancing coils C′E by a corresponding compensating coil at FP on the other side of the bridge-wire. The compensating coils are made of platinum, also annealed at a red heat, and each is placed in the box in close proximity to the coil it is intended to compensate. Each balancing coil and its compensator are tested together at various temperatures between 10° and 30° C., and are adjusted until their difference remains constant for any small variation of temperature in the neighbourhood of 20° C. This method of compensation was applied by the writer in 1887, but has not been generally adopted on account of the labour involved in adjusting the coils. The absolute values of the resistances are immaterial, but it is necessary to know the relative values with the greatest possible accuracy. For this reason it is preferable to arrange the resistances in the binary scale, each resistance being equal to twice the next smaller resistance, or to the sum of all the smaller resistances, the two smallest resistances being made equal. This arrangement permits the greatest accuracy of comparison in the simplest manner with the fewest observations. The bridge-wire EF provides a continuous scale for reading small changes of resistance. Any change of resistance of the pyrometer coil necessitates the movement of the balance point D through an equivalent resistance along the bridge wire. The equivalent resistance of the bridge-wire per unit length of the attached scale is preferably adjusted, by means of a shunt shown in parallel with it in fig. 5, to be an exact submultiple of the smallest resistance coil. It is usual also to adjust the resistances of the thermometers so that their fundamental intervals are convenient multiples of this unit, generally either 100, 200, 500, or 1000, so that the bridge-wire may read directly in degrees of temperature on the platinum scale. It is easy to get a scale of 10 cms. or more to the degree, and it is not difficult with a suitable galvanometer to read to the ten-thousandth part of a degree. The length of the bridge-wire itself need not be more than 20 or 30 cms., as the balancing resistances enable the scale to be indefinitely extended. Thus the instrument possesses the great advantage over the mercury thermometer that the most open scale may be easily secured without unwieldy length, and without restricting the range of each thermometer.
26. Errors and Corrections.—It is most instructive to consider the errors and corrections involved in platinum thermometry on the same lines as those on which the corresponding errors of the mercury thermometer have already been treated.
I. The changes of zero of the mercury thermometer arise chiefly from the small expansibility of mercury combined with the imperfect elasticity of the containing tube. In platinum thermometry the containing tube has nothing to do with the reading, and the effect of any possible strain of the fine wire of the coil is minimized by its small dimensions and by the large temperature-coefficient of the increase of resistance, which is more than twenty times greater than the coefficient of apparent expansion of mercury in glass. It is not surprising, therefore, that the changes of zero of a platinum thermometer should be practically negligible, provided that the wire is not strained and contaminated with impurities. It is probable that with ordinary care the changes of zero due to exposure to any given limits of temperature are in all cases less than the limit of accuracy of observation, due to other causes at the extreme limit of the range considered.
II. The fundamental interval of each thermometer must be determined as usual by observations in ice and steam, and a correction must be applied by the method already described in the case of the mercury thermometer. The difference of the temperature of the steam from 100° C. should be determined on the platinum scale by the approximate formula
| dpt1=·985dt1=·0362 (H−760) −·000020(H−760)2 | (26) |
III. Pressure Correction.—The effect of change of pressure on a platinum thermometer of the ordinary tube form is of course nothing, as the wire itself is not exposed to the pressure. Even if the wire is naked and directly exposed to large changes of pressure, the change of reading is almost inappreciable. Similarly there is no source of error analogous to the effects of capillarity, which are so troublesome with delicate mercury thermometers.
IV. Stem Exposure.—The reading of a platinum thermometer with compensated leads depends only on the temperature of the coil of wire forming the bulb, and not on the temperature of the stem, provided that the immersion is sufficient to avoid errors due to conduction or convection along the stem. It is desirable that the top of the bulb should be immersed to a depth equal to from three to ten times the diameter of the tube, according to the accuracy required.
V. Scale Correction.-The reduction to the thermodynamical scale may be effected, within the limits of probable error of the most accurate measurements at present available, by the very simple difference formula (25) already given, over the whole range from −100° C. to +1100° C. This is in striking contrast with the mercury thermometer, which requires a cubic formula to cover the range 0° to 200° C. with equal accuracy. The value of the constant d in the formula Varies but little, provided that the wire be fairly pure and the thermometers properly constructed. In order to determine its value in any special case, it is best to take an observation at the boiling-point of sulphur (S.B.P.) for temperatures above 0° C., or at that of oxygen for temperatures below 0° C. down to −200° C. It appears probable that there is a point of inflection in the curve of resistance-variation of platinum and some other metals in the neighbourhood of −200° C., and that the formula does not apply accurately below this point. It has become the custom to assume the boiling-point of sulphur (S.B.P.) under normal pressure to be 444·53° C., as determined by Callendar and Griffiths, using a constant-pressure air thermometer, and to take the rate of change of temperature with pressure as ·082° per mm. from Regnault's observations. According to experiments made at Kew Observatory with platinum thermometers (Chree, Proc. R. S., 1900), the rate of change is somewhat larger than that given by Regnault's formula, namely, about 090° per mm., and it appears desirable to determine this constant with greater accuracy. The difference between the above formulae reaches a tenth of a degree if the barometer differs by 12 mm. from 760 mm. The uncertainty in the absolute boiling-point of sulphur, however, is probably somewhat greater than one-tenth of a degree, on account of the uncertainty of the expansion correction of the gas thermometer (Phil. Mag., December 1899). The thermodynamical correction of the gas thermometer, which amounts to half a degree at this point, is also to some extent uncertain, on account of the extrapolation. Provided, however, that some exact value of the S.B.P. is chosen for reference, for the reduction of observations with platinum thermometers, the results so reduced will be strictly comparable, and can be corrected at any subsequent time when the value of the S.B.P. is more accurately determined. The boiling-point of oxygen may be taken as −182·5° C. with sufficient approximation for a similar purpose.
VI. Calibration Correction.—The calibration of the resistance box and the bridge-wire corresponds to the calibration of the stem of the mercury thermometer, but the process is much simpler for several reasons. It is more easy to obtain a uniform wire than a uniform tube. The scale of the wire is much more open, it corresponds to a very small part of the whole scale, and the process of calibration is easier. One box when calibrated will serve for any number of thermometers of different ranges and scales, and covers the whole range of temperature (see Calibration).
27. Electrical Precautions.—The platinum thermometer is so far superior to the mercury thermometer in all the points above enumerated that, if there were no other difficulties, no one would ever use a mercury thermometer for work of precision. In using a platinum thermometer, however, some electrical training is essential to obtain the best results. The manipulation and adjustment of a delicate galvanometer present formidable difficulties to the non-electrical observer. Bad contacts, faulty Connexions, and defective insulation, are not likely to trouble the practised electrician, but present endless possibilities of error to the tyro. A useful discussion of these and similar details is given in the paper by Chree already referred to. Bad insulation of the pyrometer and connexions can easily be detected, in the compensated instrument already described, by disconnecting one of the C leads from the battery and one of the P leads from the bridge-wire. Under these conditions the galvanometer should not deflect if the insulation is perfect. Defective insulation is most likely to be due to damp in the thermometer at low temperatures. This source of error is best removed by drying and hermetically sealing the thermometers. Trouble from bad contacts generally arises from the use of plugs for the -resistance coils. If plugs are used, they must be specially designed so as not to disturb each other, and must be well fitted and kept very clean. Mercury cups with large copper terminals, well amalgamated, as used with standard resistance coils, are probably the simplest and most satisfactory method of changing connexions. Accidental thermoelectric effects in the circuit are a possible source of error, as with the thermocouple, but they are always very small if the thermometer is properly constructed, and are relatively unimportant owing to the large E.M.F. available. In any case they may be completely eliminated by reversing the battery. The heating effect of the current through the thermometer is often negligible, but should be measured and
| |
| Fig 7.—Platinum Thermometer. |
allowed for in accurate work. With a current of ·01 ampere the rise of temperature should not exceed 1100 or 2100 of a degree. With a delicate galvanometer it is possible to read to the ten-thousandth of a degree with a current of only ·002 ampere, in which case the heating effect is generally less than 11000 of a degree. It can be very easily measured in any case by changing from one cell to two, thus doubling the current in the thermometer, and quadrupling the heating effect. The correction is then applied by subtracting one-third of the difference between the readings with one and two cells from the reading with one cell. The correction is always very small, if a reasonably sensitive galvanometer is used, and is frequently negligible, especially in differential work, which is one of the most fruitful applications of the platinum thermometer.
28. Construction of Thermometers.-One of the chief advantages of the platinum thermometer for research work is the endless variety of forms in which it may be made, to suit the particular exigencies of each individual experiment. It is peculiarly suited for observing the average temperature throughout a length or space, which is so often required in physical experiments. For this purpose the wire may be disposed in a straight length, or in a spiral, along the space in question. Again, in observing the temperature of a gas, the naked wire, on account of its small mass and extremely low radiative power, is far superior to any mercury thermometer. The commonest form of platinum thermometer (fig. 7), and the most Platinum suitable -for general purposes, contains a coil B from 12 in. to 2 in. long, wound on a cross of thin mica, and enclosed in a tube, about 14 to 12 in. in diameter, of glass or porcelain according to the temperature for which it is required. The pyrometer leads and the compensator leads are insulated and kept in place by passing through mica disks fitting the tube, which serve also to prevent convection currents up and down the tube. The protecting tube of glass or porcelain is fitted with a wooden head A carrying our insulated terminals, PP, CC, to which the pyrometer and compensator leads are respectively connected, and which serve to connect the instrument to the measuring apparatus; For work of the highest precision these terminals are often omitted, and the leads are directly soldered to a flexible cable in order to avoid possible errors from thermoelectric effects and changes of resistance of the screw terminals. For temperatures above 500° C. the protecting tube must be of porcelain, and the leads of platinum throughout that part of the tube which is exposed to high temperatures. For lower temperatures a tube of hard glass and leads of copper or silver may be employed, but it is better in any case to make the lower part of the leads of platinum in order to diminish the conduction of heat along the stem. For laboratory work a tube 30 or 40 cm. in length usually suffices, but for large furnaces the length of the protecting tube is often 5 to 10 ft. In the latter case it is usual to protect the porcelain tubes with an external steel tube, which may be removed for delicate measurements.
29. Special Forms of Thermometer.—In the measurement of linear expansion it is a great advantage to employ a thermometer with the bulb or sensitive portion equal in length to the bar or column under test, so as to obtain the mean temperature of the whole length. In measuring the linear expansion of a standard metre or yard, a fine platinum wire enclosed in a glass capillary, or otherwise insulated, is employed, its length being equal to that of the bar. The same method has been applied by Callendar (Phil. Trans. A, 1887) and Bedford (Phil. Mag., 1898) to the expansion of glass and porcelain at high temperatures, employing a fine wire supported along the axis of the tube under test. An equivalent method, applied to the expansion of silica by Callendar, is to enclose a rod of the material inside a platinum tube which is heated by an electric current. This is a very rapid and convenient process, since the mean temperature of the rod must be equal to that of the enclosing tube. Any temperature up to the melting-point of platinum is readily obtained, and easily regulated. The temperature may be obtained by observing either the resistance of the platinum tube or its linear expansion. Either method may also be employed in J. Joly’s meldometer, which consists of an electrically heated strip for observing the melting-points of minerals or other substances in small fragments. In observing the temperature of a long column of mercury, as in the method of equilibrating columns for determining the absolute expansion of mercury, a platinum thermometer with a bulb equal in length to the column may similarly be employed with advantage. The application is here particularly important because it is practically impossible to ensure perfect uniformity of temperature in a vertical column, 6 ft. or more in length, at high temperatures.
30. Sensitive Thermometers.—Where quickness of reading is essential, the mercury thermometer, or the tube form of electric thermometer, is unsuitable. In cases where the thermometer has to be immersed in a conducting liquid or solution, the fine wire forming the bulb may be insulated by enclosing it in a coiled glass capillary. This method has been employed by Callendar and Barnes and by Jaeger, but the instrument is necessarily fragile, and requires careful handling. For non-conducting liquids or gases the bare wire may be employed with great advantage. This is particularly important in the case of gases owing to the extreme sensitiveness thus obtained and the almost complete immunity from radiation error at moderate temperatures. Thermometers constructed in the form of a flat grid of bare wire mounted on a mica and ebonite frame have been employed by H. Brown (Proc. R. S., 1905, B 76, p. 124) for observing the temperature of leaves and of air currents to which they were exposed. They have also been employed for observing the air-temperature for meteorological purposes in Egypt and Spain with very satisfactory results (Proc. R. S., 1905, A 77, p. 7). The fine wire, owing to its small size and bright metallic surface, very rapidly acquires the temperature of the air, and is very little affected by radiation from surrounding objects, which is one of the chief difficulties in the employment of mercurial thermometers for the observation of the temperature of the air.
For the observation of rapidly varying temperatures, such as those occurring in the cylinder of a gas- or steam-engine, an electrical thermometer with very fine wire, of the order of .001 in. diameter is practically the only instrument available. The temperature at any particular moment may be obtained by setting a mechanical contact-maker to close the circuit at the desired point. The sensitive part of the thermometer consists simply of a loop of fine wire from half an inch to an inch long, connected by suitable leads to the measuring apparatus as employed by Burstall (Phil. Mag., October 1895) in the gas-engine, and Callendar and Nicolson (Proc. Inst. C. E., 1898) in the steam-engine. The explosion temperatures cannot be satisfactorily measured in a gas-engine in this manner, because the radiation error at high temperatures is excessive unless the wire is very fine, in which case it is very soon melted even with weak mixtures. Callendar and Dalby accordingly devised a mechanical valve (Proc. R. S., A 80, p. 57) for exposing the thermometer only during the admission and compression strokes, and have deduced the actual explosion temperatures from the indicator diagram. B. Hopkinson (Proc. R. S., A 77, p. 387) succeeded in following the course of an explosion in a closed vessel by means of a similar thermometer connected to a galvanometer of short period giving a continuous record on a moving photographic film. When the flame reached the wire the temperature rose 1200° C. in about 150 of a second, which illustrates the order of sensitiveness attainable with a fine wire of this size. O. R. Lummer and E. Pringsheim, in their measurements of the ratio of the specific heats of gases by observing the fall of temperature due to sudden expansion, employed a very thin strip of foil with the object of securing greater sensitiveness. This was a somewhat doubtful expedient, because such a strip is extremely fragile and liable to be injured by air currents, and because the sensitiveness is not as a matter of fact appreciably improved, whereas the radiation error is increased in direct proportion to the surface exposed. One of the principal sources of error in employing a short loop of fine wire for observing rapidly varying temperatures is that the ends of the loop close to the thick leads are affected by conduction of heat to or from the leads, and cannot follow the rapid variations of temperature. This error may be readily avoided by the method. first employed by Callendar and Nicolson, of connecting the compensating leads with a short length of the same fine wire. The end effect is then eliminated by observing the difference of resistance between two loops of different lengths. Thermocouples of very fine wire have also been employed for similar measurements, but they are more difficult to make than the simple loop of one wire, and the sensitiveness attainable is much less, owing to the small E.M.F. of a single thermocouple.
31. Radiation Thermoscopes.—For measuring the intensity of radiation, some form of thermometer with a blackened bulb or sensitive area is employed. It is assumed that the rise of temperature of the thermometer is approximately proportional to the intensity of the radiation according to Newton’s law of cooling (see HEAT) for small differences of temperature. A mercury maximum thermometer with a small blackened bulb is still very generally employed in meteorological observatories for registering the maximum solar radiation. But the indications are liable to error and very difficult to interpret, and an instrument of this type is not sufficiently sensitive or quick in action for weak sources of radiation. Sir John Leslie employed an air Thermoscope, similar to that of Galileo (Heat, fig. 1), with a blackened bulb. This has the advantage of a small capacity for heat, and is still employed in various forms for demonstration purposes, but is not sufficiently sensitive for accurate work. Electrical thermometers are now generally employed on account of their superior sensitiveness, and also on account of the greater facility of adaptation for the requirements of each particular experiment. The most familiar instrument is M. Melloni’s thermophile, which is built up of a number of small bars of antimony and bismuth, or other alloys of high thermoelectric power, arranged in the form of a cube with alternate junctions on opposite faces. When connected to a galvanometer of suitable resistance, this arrangement gives a high degree of sensitiveness on account of the multiplication of couples, but owing to the large mass of metal involved in its construction it takes a considerable time to acquire a steady state. This defect has been remedied in the radiomicrometer of C. V. Boys (Phil. Trans., 1888, 180 A, p. 159) by employ in a single junction attached to a small disk of very thin copper. The free ends of the minute bars forming the couple are connected to a loop of thin copper wire suspended by a fine quartz fibre between the poles of a magnet. This arrangement forms a very delicate galvanometer and gives the maximum sensitiveness attainable with a single couple, since all unnecessary connecting wires are avoided. It is incomparably quicker and more dead-beat in action than the ordinary thermophile, but has the disadvantage that it must be set up permanently on a steady support and the radiation brought to it in a horizontal direction. An instrument of similar delicacy is the radiometer, the action of which depends on the repulsive effect of the residual gas in a nearly perfect vacuum on a delicately balanced vane suspended by a fine fibre. An instrument of this type was first constructed by Sir William Crookes (see Radiometer); the instrument was applied to radiation measurements, and its sensitiveness greatly improved by E. F. Nichols. It requires a very steady mounting, like the radio micrometer, but has the additional defect that the radiation must be introduced through a window, which may give rise to selective absorption. Other varieties of thermophile, in which the sensitive parts are constructed, as in Boys’ radiomicrometer, so as to have a very small capacity, but are connected like the ordinary pile to a separate galvanometer, have been employed by Lord Rosse for observations of lunar heat and by W. H. Julius and Callendar for the solar corona.
In cases where the radiation can be concentrated on a very small area, such as the receiving disk of the radio micrometer, the thermoelectric method is probably the most sensitive. But if there is no restriction as to the area of the receiving surface, considerable advantage may be gained in convenience of manipulation, without loss of sensitiveness, by the electric resistance method. An instrument of this type was first employed by S. P. Langley (Proc. Amer. Acad., 1881, 16, p. 342) under the name of the bolometer, by which it has since been known. The sensitive surface is made in the form of a blackened grid of thin metallic foil, generally platinum coated with platinum black, connected in one of the arms of a Wheatstone bridge. The rise of temperature of the grid when exposed to radiation is measured by its increase of resistance in the usual manner. In order to compensate for changes of temperature of the surrounding air the balancing resistance is made of a precisely similar grid, placed in close proximity to the first but screened from radiation. The foil should be as' thin as possible consistent with strength, in order to secure the maximum sensitiveness. For spectroscopic work a single strip or linear bolometer is employed. For absolute measurements, where it is necessary to absorb the whole radiation admitted through a given area, two grids are placed with the strips of one behind the inter-spaces of the other.
32. Absolute Measurement of Radiation.—In many eases the object is not to secure the maximum degree of sensitiveness, but an absolute measurement of the intensity of the radiant enery in calories per square centimetre per minute, or other suitable units. For this purpose some form of radiation thermometer is generally employed, but the method of procedure is modified. The earlier methods as exemplified in C. S. M. Pouillet’s pyrheliometer, or L. J. G. Violle’s actinometer, consisted in observing the rate of rise of temperature of a small calorimeter, or thermometer of known thermal capacity, when exposed to a given area of the radiation to be measured. To secure greater sensitiveness A. P. P. Crova substituted a copper disk with an attached thermocouple for the colorimetric thermometer. The method is very simple and direct, but has the disadvantage that the correction for external loss of heat is somewhat uncertain and difficult to apply, since the conditions are unsteady and the observation depend; on rate of change of temperature. For this reason static methods, depending on the steady temperature finally attained, in which the rate of loss of heat is directly determined by an electric compensation method, h ve come more prominently into favour in recent years. In K. J. Ångström’s pyrheliometer (Acta Soc. Upsala, 1893), two similar blackened strips of equal area and resistance are fixed side by side in a suitable case in such a manner that either may be exposed to the radiation to be measured while the other is simultaneously heated by an electric current. Attached to the backs of the strips, but insulated from them by thin paper, are the two junctions of a thermocouple which indicates when the temperatures are equal. When this condition is secured the intensity of the radiation is equal to the rate of generation of heat per unit area by the electric current, which is deduced, from a knowledge of the resistance and area of the strip, by observing the current required to balance the radiation. The instrument is very quick and sensitive in action, and the method avoids any assumption with regard to the rate of loss of heat, except that it is the same for the two similar strips at the same temperature. The accuracy of the method is limited chiefly by the measurement of the resistance and width of the strips, and by the difficulty of securing exact similarity and permanence in the attachment of the junctions of the thermocouple. Small differences in this respect may be eliminated by interchanging the strips, but there remain outstanding differences between different instruments of the same make which often exceed 5 per cent.
An electric method proposed by F. Kurlbaum (Wied. Ann., 1898, 65, p. 748) consists in observing the rise of temperature produced by radiation in a bolometer grid, then cutting off the radiation and observing the increase of current required to produce the same rise of temperature. There is no difficulty in this case in measuring the area exposed or the resistance of the bolometer, and no uncertainty can arise as to the temperature of the strip, because the heated strip itself serves as its own thermometer. The current is easily deduced from a knowledge of the resistances and the E.M.F. of the battery. The chief source of uncertainty mentioned by Kurlbaum lies in possible differences between the effects of radiation and current-heating near the ends of the strips, the area so affected representing a large proportion of the whole area. In Ångström’s method this is not so important because the temperature indicated by the couple is that near the middle of the strip. In the case of the bolometer this end-effect may be compensated, as explained by Callendar (Proc. R. S., 1907, 77 A, p. 7), in the same manner as for sensitive thermometers, by employing two similar bolometers with strips of different lengths.
An important defect of all the methods so far considered is that the measurement de ends on the coefficient of absorption of the black with which the receiving surface is coated. The error is probably small, of the order of I or 2 per cent., but is difficult to determine accurately, and varies to some extent with the quality of the radiation. The absorptive power is generally less for /rays of great wave-length than for visible rays. if we assume that the loss of heat by conduction and convection is independent of the nature of the surface the defect in question may be avoided by the following method. Two bolometer strips, one bright and the other black, but otherwise exactly similar, are simultaneously exposed to the radiation to be measured, and are traversed by the same electric current. The black strip .will be more heated by the radiation than the bright, but the rise of temperature of the bright strip due to the current will be greater than that of the black strip because its emissive power is lower. If the current is adjusted until the temperatures of the two strips are equal the losses by convection and conduction-will be equal, and also the rate of generation of heat by the current in each strip. The rise of temperature must therefore be such that each strip loses as much heat by radiation to the surrounding case as it gains from the incident radiation to be measured. Assuming Kirchhoff’s law, the ratio of the emissive to the absorptive power is the same for all bodies at the same temperature, and is equal to the emissive power of a perfectly black body. The rise of temperature of each strip, when balance is attained, will be the same as that of a perfectly black strip under the same conditions of exposure. The electric current in this method serves to eliminate losses by convection and conduction, and the result is obtained in terms of the observed rise of temperature and the radiation constant for a black body. The method works well for a source at 100° C.; but, for a high temperature source, a correction is required because the absorptive powers of the strips may differ appreciably from their emissive powers.
Another electric compensation method of special interest is the method of the “Peltier cross,” A small disk of copper is supported by two thermoelectric couples forming a cross. One of the couples serves to measure the rise of temperature, while the other is traversed by an electric current, which may be employed to compensate the radiation by the heat absorption due to the Peltier effect. The advantage of this method is that the Peltier effect is easily determined from an observation of the thermoelectric power {see Thermoelectricity) in absolute measure, and that it is proportional to the first power of the current. Loss or gain of eat by conduction from the supporting wires, and changes of temperature in the surrounding case, are readily compensated by mounting two similar disks side by side. Small differences between the disks are eliminated by exposing them to radiation alternately, with reversal of the current, so that the irradiated disk is cooled or the other disk heated by the Peltier effect. The current is adjusted in each case so that the temperatures of the disks are equal, as indicated by the second couple connecting the disks. The method is about equal in sensitiveness to that of Ångström, but it is easier to secure conditions of exact similarity and to measure the quantities involved in the absolute determination, namely, the area of the hole through which the radiation is admitted, and the coefficient of the Peltier effect. The uncertainty due to imperfect blackness of the disks may be eliminated by using cups. in place of disks; and the sensitiveness and range may be increased by using thermopiles in place of single couples.
35. Optical or Radiation Pyrometers.—-Since the intensity of radiation increases very rapidly with the temperature of the source of radiation, instruments for measuring radiation may be applied for measuring temperature, assuming that the laws connecting radiation an temperature are known. The advantage of this method is that the measurement may be made from a distance without exposing any part of the measuring apparatus to the destructive action of high temperatures. Apart from the difficulty of calibrating the measuring apparatus to give temperature in terms of radiation, the chief source of uncertainty in the application of the method is the emissive power of the source of radiation. The methods principally employed may be divided into two classes:-(1) Radiation methods, depending on the measurement of the radiant energy by means of a radiometer, thermocouple or bolometer; (2) optical or photometric methods, depending on the colour or luminous intensity of the radiation as compared with a. suitable standard.
Of the radiation methods the simplest in theory and practice depends on observing the total intensity of radiation, which) varies as the fourth power of the absolute temperature according to the Stefan-Boltzmann law (see Heat) for a perfectly black body or full radiator. In applying this method it is very necessary to allow for the emissive power of the source, in case this does not radiate as a black body. Thus the emissive power of polished platinum at 1000° Abs. is only 10 per cent., and that of black iron oxide about 40 per cent. of that of a black body; and the percentage varies differently for different bodies with change of temperature, and also for the same body according to the part of the spectrum used for the measurement. Owing to the rapid increase of radiation with temperature the error due to departure from black body radiation is not so serious as might be imagined at first sight. If the temperature of a polished platinum strip at 1500°C. were estimated by the radiation formula, assuming the constant for a perfectly black body, the error for red light would be about 125°, for green about 100°, and for blue about 75°. Such errors may be corrected when the emissive power of the source at various temperatures is known from previous experiments, but it is preferable to observe, whenever possible, the radiation from the interior of a uniformly heated enclosure which approximates very closely to that of a black body (see Heat).
Radiation pyrometers of this type are generally calibrated by the method of sighting on the interior of an electric furnace containing a thermocouple or gas-thermometer by which the temperature is measured. The gas-thermometer has been employed for verifying the law of radiation up to 1500° C. but the difficulties of obtaining accurate results with the gas-thermometer increase so rapidly above 1200° C. that it is questionable whether any advantage is gained by using it beyond this point. The law of radiation has been so closely verified by observations at lower temperatures that the uncertainty involved in applying it at higher temperatures, in the case of a black body is probably less than the uncertainty of the gas-thermometer measurements, and much less than the uncertainty of extrapolating an empirical formula for a thermocouple. Thus L. F. C. Holborn and W. Wien (Wied. Ann., 1895, (6), by extrapolating their thermoelectric formula, found the value 1587°C. for the melting-point of palladium, whereas Violle found 1500°C. by the colorimetric method, and Callendar and Eumorfopoulos (Phil. Mag., 1899, 48) found 1540° and 1550°C. by the methods of the expansion and the change of resistance of platinum respectively. By a later thermoelectric extrapolation Holborn and Henning (Berlin Akad., 1905, 12, p. 311) found 1535°C. for the melting-point of palladium, and 1710°C. for that of platinum, values which were strikingly confirmed by J.A. Harker at the National Physical Laboratory, and by Waidner and Burgess at the Bureau of Standards, U.S.A. Holborn and Valentiner employing an optical method (Ann. Phys., 1907, 22, p. 1) found 1582°C. and 1789° C. for palladium and platinum respectively. There can be little doubt that the extrapolation of the parabolic formula for the thermocouple at these temperatures is quite untrustworthy (see Thermoelectricity) and that the values given by the electrical resistance method, or by the laws of radiation, are more likely to be correct. Assuming that the total radiation varies as the fourth power of the absolute temperature, a radiation pyrometer can be calibrated by a single observation at a known temperature, such as the melting-point of gold, IO62° C. if a black body is employed as the source; and its indications will probably be accurate at higher temperatures under a similar restriction. If the pyrometer is sighted on the interior of a furnace through a small observation
An image should appear at this position in the text. If you are able to provide it, see Wikisource:Image guidelines and Help:Adding images for guidance. |
fig 8.—Féry's Mirror Pyrometer (Camb. Scient. Inst. Co.). For temperatures from 500° C. to 1100°C
hole it will indicate the temperature of the furnace correctly, provided that the temperature is uniform. But it must be remembered that this condition does not generally exist in large furnaces, Suppose, for instance, that it is required to find the temperature of the molten metal on the hearth of a furnace viewed through a thick layer of furnace gases, which are probably at a much higher temperature. It is evident that the radiation from the intervening flame may be much greater than that from the metal, and may introduce serious errors. The same objection applies with greater force to optical pyrometers, as the luminous radiation from gases may be of a highly selective character. If, on the other hand, it is required to observe the temperature of metal in a ladle before casting, the surface of the metal must be cleared of scum, and it is necessary to know the emissive power of the metal or oxide exposed.
For scientific measurements of temperature by the radiation method, the thermophile, or bolometer, or radio micrometer. previously calibrated by exposure to a black body at a known temperature, is directly exposed at a known distance to a known area of the source of radiation. The required result may then be deduced in terms of the area and the distance. The use of extraneous optical appliances is avoided as far as possible on account of selective absorption. For practical purposes, in order to avoid troublesome calculations and measurements, an optical arrangement is employed, either lens or mirror, in order to form an image of the source on the receiving surface. Fig. 8 illustrates Féry's mirror pyrometer, in which a mirror M, focused by the pinion P, forms an image of the source on a. disk, supported by wires of constant an and copper forming a thermocouple, connected by the brass strips D and R to the terminals b, b'. The observation hole in the wall of the furnace is sighted through the eyepiece O, and is made to overlap the disk slightly. The rise of temperature of the junction is assumed to be (proportional to the intensity of radiation, and is indicated by the deflexion of a delicate galvanometer connected to the terminals b, b'. A lens may be substituted for the mirror at high temperatures, but it is necessary to allow for the selective absorption of the lens, and to a less extent, for that of the mirror, by a special calibration of the scale.
Assuming Wein's laws for the distribution of energy in the spectrum (see Heat), the, temperature of a black body may also be measured by observing (1) the wave-length corresponding to maximum intensity in the normal spectrum, which varies inversely as the absolute temperature, or (2) the maximum intensity itself, which varies as the fifth power of the absolute temperature, or (3) the intensity of radiation corresponding to some particular radiation or colour, which varies as an exponential function, the exact form of which is somewhat uncertain. Methods (1) and (2) require elaborate apparatus and are impracticable except for purposes of scientific research. The exact application of method (3) is almost equally difficult, and is less certain in its results, but for optical purposes this method may be realized with a fair degree of approximation by the use of coloured glasses, and forms the basis in theory of the most trustworthy optical pyrometers.
34. Optical or Photometric Pyrometers.—The change of colour of a heated body from red to white with rise of temperature, and the great increase of intrinsic brilliancy which accompanies the change, are among the most familiar methods of estimating high temperatures. For many processes eye estimation suffices, but a much greater degree of accuracy may be secured by the employment of suitable photometers. In Mesuré and Nouel's pyrometric telescope, the estimation of temperature depends on observing the rotation of a quartz polarimeter required to reduce the colour of the radiation to a standard tint. It has the advantage of requiring no auxiliary apparatus, but, owing to the lack of a standard of comparison, its indications are not very precise. In the majority of photometric pyrometers, a standard of comparison for the intensity of the light, either an amyl-acetate or gasoline lamp, or an electric glow-lamp, is employed. The optical pyrometer of H. L. Le Chatelier (Compter Rendus, 1892, 114, p. 214) was one of the earliest, and has served as a model for subsequent inventors. The standard of comarison is an amyl-acetate lamp, the flame of which is adjusted) in the usual manner and viewed in the same field as the image of the source. The two halves of the field are adjusted to equality of brightness by means of a cat's eye diaphragm and absorption glasses, and are viewed through a, red glass, giving nearly monochromatic radiation in order to avoid the difficulty of comparing lights of different colours. Assuming Wien's law, the logarithm of the intensity of monochromatic radiation for a black body is a linear function of the reciprocal of the absolute temperature, and the instrument can be graduated by observing two temperatures; but it is generally graduated at several points by comparison with temperatures observed by means of a thermocouple.
The Wanner Pyrometer (Phys. Zeits., 1902, p. 112) is a modification of Konig's spectrophotometer, in which the two halves of the field, corresponding to the source and the standard of comparison, are illuminated with monochromatic red light polarized in planes at right angles to each other. The two halves may be equalized by rotating the analyzer, the circle of which is graduated to read in degrees of temperature. The instrument has a somewhat restricted range of maximum sensitiveness, and cannot be used below 900°C. owing to the great loss of light in the complicated optical system. It cannot be sighted directly on the obyect since no image is formed as in the Le Chatelier or Féry instruments, but the methods of securing monochromatic light by a direct vision spectroscope, and of adjusting the fields to equality by rotating the analyser, are capable of great precision, and lead to simple theoretical formulae for the ratio of the intensities in terms of Wien's law.
The Féry Absorption Pyrometer (Journ. Phys., 1904, p. 32) differs from Le Chatelier's only in minor details, such as the replacement of the cat's eye diaphragm by a pair of absorbing glass wedges. The principles of its action and the method of calibration are the same. The pyrometers of Morse, and of L. F. C. Holborn and F. Kurlbaum depend on the employment of a glow lamp filament as standard of comparison, the current through which is adjusted to make the intrinsic brilliancy of the filament equal to that of the source. When this adjustment is made the filament becomes invisible against the image of the source as background, and the temperature of the source may be determined from an observation of the current required. Each lamp requires a separate calibration, but the lamps remain fairly constant provided that they are not overheated. To avoid this, the source is screened by absorption glasses (which also require calibration) in observing high temperatures. Except at low temperatures the comparison is effected by placing a red glass before the eyepiece. At low temperatures a special advantage of the glow-lamp as a standard of comparison is that it matches the source in colour as well as in brightness, so that the instrument is very sensitive. At high temperatures the red glass serves chiefly to mitigate the glare.
35. Registering and Recording Thermometers.—The term registering thermometer is usually applied to an instrument with an index which requires setting, and when set will indicate the maximum or minimum temperature occurring, or will register the temperature at a particular time or place. A recording instrument is one constructed to give a continuous record of the temperature, and requires a revolving drum or some equivalent clockwork mechanism for recording the time. The most familiar types of registering thermometers are modifications of the common liquid-in-glass thermometer.
John Rutherford's maximum, invented before 1790, was an ordinary mercurial thermometer placed horizontally; the column pushed before it a small steed index which was left at the highest point reached and was drawn down again to the liquid by a magnet when the instrument had to be reset. It is little used now. Negretti and Zambra's maximum has a constriction in the tube near the bulb, past which the mercury easily expands but cannot return when the temperature falls, since the column breaks at the narrowed point when the fluid in the bulb begins to contract. The instrument is set for a fresh observation by shaking the detached portion of the column back down the tube. The clinical thermometers used by physicians are instruments of this type, and are made with a very open scale to read only in the neighbourhood of the normal temperature of the human body. In the»Phillips or Walferdin maximum a portion of the mercury is separated from the rest by a minute bubble of air. It is placed horizontally and as the temperature rises the detached portion of the column is pushed forward but is not withdrawn when the main column retreats towards the bulb in cooling. It is set for a new observation by bringing it into a vertical position and tapping it slightly. By reducing the length of the index and the bore of the stern this thermometer may be made suitable for use in any position without altering its register.
The minimum thermometer in most common use is that of Rutherford, invented in 1790. It is a spirit thermometer, preferably filled with amyl alcohol, to 'reduce risk of distillation, in the column of which a small porcelain index is included. The instrument is hung horizontally, and, as the temperature falls, the index is drawn back through surface tension by the end of the column. When the temperature rises the liquid flows past the index, which is left at the lowest point attained. To prepare the instrument for a fresh observation it is inverted, when the index falls back against the end of the column. James Six's combined maximum and minimum thermometer (Phil. Trans., 1782) consists of a U-tube, the bend of which is filled with mercury. One leg contains spirit above the mercury and terminates in a bulb also full of spirit. The other leg also contains a column of spirit above the mercury, but terminates in a bulb containing air and vapour of spirit mixed. With increase of temperature the spirit in the full bulb expands; the mercury in consequence is pushed round the bend and rises to a greater or less extent in the other leg, carrying before it a steel index which thus marks the maximum temperature. With cold the spirit in the full bulb contracts, and the mercury moves back carrying with it a second index which marks the minimum temperature. The instrument is set by drawing down the two indices upon the two ends of the mercury column by means of a magnet.
With a mercury thermometer a continuous record of temperature can only be obtained by the aid of photography, a method which has been in use for many years at some first-class observatories, but which cannot be generally employed on account of the expense and the elaborate nature of the apparatus required. The commonest type of recording thermometer works on the principle of the Bourdon pressure-gauge. The bulb consists of a curved metallic tube filled with liquid, the expansion of which with rise of temperature tends to straighten the tube. The movements are recorded on a revolving drum by a pen carried at the end of a light lever attached to the bulb. This form of instrument is widely employed for rough work, but it. has a very limited range and is unsuitable for accurate work on account of want of sensitiveness and of great liability to change of zero, owing to imperfect elasticity of the metal tube. For accurate work, especially at high temperatures, electrical thermometers possess many advantages, and are often the only instruments available. They are comparatively free from change of zero over long periods, and the thermometer or pyrometer itself may be placed in a furnace or elsewhere at a considerable distance from the recording apparatus. The principal types are the thermocouple and the platinum resistance thermometer already described, which may be employed for recording purposes, without altering the thermometer itself, by connexion to a suitable recording mechanism. The methods in use for recording the indications of electrical thermometers may be classified as in § 24 under the two headings of (1) deflexion methods and (2) balance methods. Deflexion methods, in which the deflexion of the galvanometer is recorded, are more suitable for rough work, and balance methods for accurate measurements. The most delicate and most generally applicable method of recording the deflexions of a mirror galvanometer is by photographing the movements of the spot of light on a moving film. Almost any required scale or degree of sensitiveness may be obtained in this manner, but the record cannot be inspected at any time without removal and development. Since the forces actuating the needle of the galvanometer are very small, it is out of the question to attach a pen or marking point directly to the end of the pointer for recording a continuous trace on a revolving drum, because the errors due to friction with the recording sheet would be excessive. This difficulty has been avoided in many electrical instruments by depressing the pointer so as to mark the paper only at regular intervals of a minute or so, leaving it completely free for the greater part of the time. The record thus obtained is discontinuous, but is sufficient for many purposes. For accurate measurement, or for obtaining an open scale over a particular range of temperature, it is necessay to employ some form of balance method as already explained in § 24.
36. Electric Recorder, Balance Method.—The application of the electric balance, potentiometer or Wheatstone-bridge for recording changes of resistance or electromotive force has been effected by employing a galvanometer of the movable coil type as a relay. The delfexion of the galvanometer to right or left, according as the resistance or E.M.F. increases or diminishes, is made to actuate one or other of a pair of motors for moving the contact point on the bridge wire and the recording pen on the drum in the corresponding direction. A continuous record free from friction error is thus obtained, since the galvanometer does not actuate the pen directly. With an electrical resistance thermometer it is possible in this way to obtain continuous pen-and-ink records on a scale of an inch or more to the degree, reading to -01°C. and practically free from zero error over any desired range from -200° to +1500°C. With a thermocouple, employing the potentiometer method, the same apparatus can be used with advantage, but it is not possible to obtain so open a scale on account of the smallness of the thermoelectromotive force available.
The attainment of sufficient delicacy in the relay mechanism turns on the employment of a rotating or vibrating contact in combination with a moving coil galvanometer of the siphon recorder type. This was first successfully effected by Callendar (Trans. R. S. Canad., 1897) for records of radiation and temperature, and has since been applied to submarine telegraphy by S. G. Brown and by A. Muirhead. The mechanism of (Callendar's electrical recorder, as arranged for temperature measurements, is described and illustrated in Engineering, May 26, 1899, and in a treatise on Pyromelry by Le Chatelier and Boudouard. Electrical recording instruments of both types are now coming into extensive use for industrial purposes in the measurement of furnace temperatures, &c., for which they are particularly suitable, because the recording apparatus can be placed at any distance from the furnaces which may be considered most convenient, and can be connected to any one of a set of furnaces in succession whenever it is desired to obtain a record.
Authorities.—There is no special work on the subject of thermometry in English, but most of the principles and methods are described in text-books on heat, of which Preston's Theory of Heat may be specially mentioned. For recent advances in thermometry the reader should consult the original papers, the most important of which have been cited. The greater part of the recent work on the subject will be found in the publications of the Bureau International des Poids et Mesures de Sèvres (Paris), of the Reichsanstalt (Berlin), of the Bureau of Standards, U.S.A. (Washington), and of the National Physical Laboratory (London). (H. L. C.)
- ↑ Hall, Trans. Amer. Inst. Elect. Eng. 1891, vol. viii. p. 226; Callendar and Nicolson, Proc. Inst. C. E. vol. cxxxi. p. 1.
