On the Conditions for the Existence of Three Shock Waves

by Subrahmanyan Chandrasekhar

Ballistic Research
Laboratory Report No. 367


Chandrasekhar/emh
Aberdeen Proving Ground, Md.
June 5, 1943

ON THE CONDITIONS FOR THE EXISTENCE OF THREE SHOCK WAVES

 

1. Statement of the problem. J. von Neumann has studied the problem of the reflection of shock waves by a rigid plane surface and finds that for a given intensity of the incident shock (as specified for instance by the ratio of the pressures $\zeta$ on the two sides of the shock front) regular refection can take place only for angles of incidence $\alpha$ less than a certain critical value $\alpha _{\mathrm {extreme} }(\zeta )$.

Fig. 1

Fig. 1

Moreover, for a value $\alpha <\alpha _{\mathrm {extreme} }(\zeta )$ two solutions are possible. It is, however, generally supposed that the solution with the smaller of the two possible values $\alpha '$ represents physically realizable solution. The reason for this supposition is that in the acoustic limit $\zeta =1$ the solution with the smaller $\alpha '$ passes continuously into what is believed to be true for the sound waves (namely $\alpha =\alpha '$).

The question arises as to what happens when $\alpha >\alpha _{\mathrm {extreme} }(\zeta )$. Von Neumann suggests that for angles of incidence of a shock wave greater than the critical value the Mach effect takes place (Fig. 2),

Fig. 2

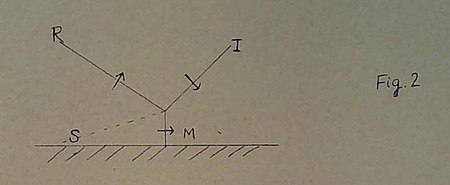
Fig. 2

in which the line of intersection of the incident and the reflected shocks no longer remains in contact with the wall but moves away from it. Under these circumstances a new shock wave $M$ (the Mach wave) is formed and moreover in the region included between the reflected $(R)$ and the Mach wave there is a surface of discontinuity $S$. Across $S$ the normal components of the velocities remain continuous while there is a discontinuity in the tangential components: in other words, $S$ is a vortex sheet. Strictly speaking, the idealization of the Mach effect in terms of plane shock waves and a plane of discontinuity $S$ cannot be valid. For at the reflecting surface (assumed rigid) the motion of the gas must be parallel to the wall and this cannot in general be accomplished on both sides of the Mach front. However, it would seem that if we are prepared to ignore this difficulty of the boundary condition on the reflecting surface behind the Mach front the idealization of the Mach effect in terms of plane shocks and a plane vortex sheet may provide a 'first' approximation to the true situation. In other words, we are led to examine the conditions under which three shock waves can be in equilibrium. In this note we shall present certain results relating to this problem.

2. The stationary Mach effect. Physical considerations would suggest that a particularly interesting case of the (idealized) Mach effect arises when the vortex sheet $S$ is parallel to the reflecting wall (Fig. 3). Such solutions may be regarded as limiting cases of the situation depicted in Fig. 2.

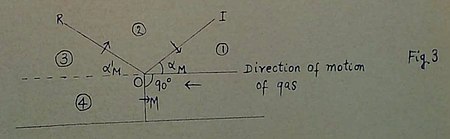
Fig. 3

Fig. 3

Moreover these solutions will represent rigorous solutions of the problem of the Mach effect in as much as for these configurations the velocity of the gas will be parallel to the reflecting surface on both sides of the Mach front.

Configurations of the type of Figure 3 can be readily isolated from the results of the theory of the regular reflection of shock waves. This can be seen as follows:

For a given intensity of the incident shock wave, the ratio of the pressures in the region behind the reflected and in front of the incident shock waves is determinate and depends only on the angle of incidence $\alpha$. On the other hand, the pressure behind the Mach front $M$ under the circumstances of Fig. 3 can also be determined (as we shall see presently) from the intensity of the incident shock wave and angle $\alpha$. Since now the regions behind the reflected and the Mach shocks are divided only by a vortex sheet the pressures behind the reflected shock derived from the theory of reflection of shock waves must agree with that computed behind the Mach shock. This will determine $\alpha _{M}$ as a function of the intensity of the incident shock.

To make the remarks in the preceding paragraph more specific, consider a frame of reference in which the point $0$ is at rest. Then the familiar equations of the Rankine-Hugoniot theory which relate the conditions on the two sides of a shock front can be parametrically represented as follows:

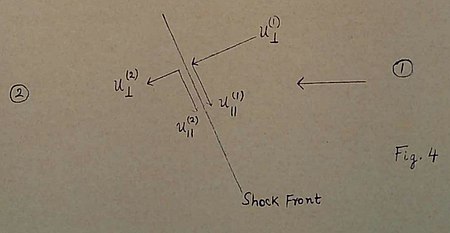
Fig. 4

Fig. 4

$\left.{\begin{array}{lll}\sigma _{\perp }^{(1,2)}={\frac {u^{(1)}-D}{c_{1}}}\\\zeta _{1,2}={\frac {P_{2}}{P_{1}}}={\frac {1}{\gamma +1}}\left\{2\gamma \left[\sigma _{\perp }^{(1,2)}\right]^{2}-(\gamma -1)\right\}\\\eta _{1,2}={\frac {\rho _{1}}{\rho _{2}}}={\frac {(\gamma -1)\left[\sigma _{\perp }^{(1,2)}\right]^{2}+2}{(\gamma +1)\left[\sigma _{\perp }^{(1,2)}\right]^{2}}}\\\tau _{\perp }={\frac {u_{\perp }^{(2)}-D}{c_{1}}}={\frac {1}{\gamma +1}}\left\{(\gamma -1)\sigma _{\perp }^{(1,2)}+2\left[\sigma _{\perp }^{(1,2)}\right]^{-1}\right\}\\c_{2}=c_{1}{\sqrt {\zeta _{1,2}\eta _{1,2}}}\end{array}}\right.$

(1)

where $c_{1}$ and $c_{2}$ denote the velocities of sound in the two regions respectively and the rest of the symbols have their usual meanings. Finally

$u_{\parallel }^{(1)}=u_{\parallel }^{(2)}$

(2)

.

In other words, if we measure the velocities in units of the velocity of sound in region $1$ then all the relevant physical quantities (including the velocity of sound in region $2$) can be expressed parametrically in terms of $\sigma _{\perp }^{(1,2)}$. As we have already stated, we shall measure the intensity of a shock wave by the ratio of the pressures on either side of the shock front, i.e., $\zeta _{1,2}$. We may note that if in a fixed frame of reference the shock is moving in the direction $2\rightarrow 1$, $\zeta _{1,2}>1$ and $\sigma _{\perp }^{(1,2)}>1$; conversely the direction of motion of a shock front can be inferred from whether $\sigma _{\perp }^{(1,2)}$ is greater than or less than unity.

Returning to the configuration of shocks depicted in Fig. 3, since $\zeta _{1,2}$ is assumed known,

$\sigma _{\perp }^{(1,2)}={\sqrt {{\frac {1}{2\gamma }}\left[(\gamma +1)\zeta _{1,2}+(\gamma -1)\right]}}.$

(3)

Hence, for the region in front of the shock

$|\sigma |=\sigma _{\perp }^{(1,2)}\mathrm {cosec} \alpha .$

(4)

For the Mach shock the appropriate value of $\sigma _{\perp }^{(1,4)}$ is $|\alpha |$.

$\left.{\begin{array}{lll}\zeta _{1,4}&={\frac {1}{\gamma +1}}\left\{2\gamma \left[\sigma _{\perp }^{(1,2)}\right]^{2}\mathrm {cosec} ^{2}\alpha -(\gamma -1)\right\}\\&={\frac {1}{\gamma +1}}\left\{\left[(\gamma +1)\zeta _{1,2}+(\gamma -1)\right]\mathrm {cosec} ^{2}\alpha -(\gamma -1)\right\}.\end{array}}\right.$

(5)

But the equality of the pressures in regions $3$ and $4$ requires that

$\zeta _{1,4}=\zeta _{1,2}\zeta _{2,3}.$

(6)

The quantity $\zeta _{2,3}$ has been plotted by von Neumann as a function of the angle of incidence $\alpha$.^[1] Accordingly the intersection of the curve $\zeta _{2,3}(\alpha )$ with $\zeta _{1,4}/\zeta _{1,2}$ determines the angle $\alpha _{M}$ at which we have what we might call the stationary Mach-effect. In this manner it is found that

$\alpha _{M}=21.75^{\circ },\quad 31.25^{\circ },\quad 42.5^{\circ }\quad {\text{for}}\quad \zeta _{1,2}=\infty ,\quad 7.0225,\quad 2$

(7)

respectively. More exact and extensive calculations of the type indicated have since been carried out by Dr. R. Seeger, whose results are summarized in Figure 5. An examination of this curve reveals that for $\zeta _{1,2}>2.26$ the stationary Mach effect occurs for an angle of incidence $\alpha _{M}$ which is less than the corresponding $\alpha _{\mathrm {extreme} }$. On the other hand for $\zeta _{1,2}<2.26$ the stationary Mach reflection occurs as a branch along the sequence of the so-called 'unstable' regular reflections. Consequently, for strong shocks with $\zeta _{1,2}>2.26$ we may expect the Mach effect to start at an angle of incidence smaller than that at which regular reflection becomes kinematically impossible. The basis for this suggestion is that we may reasonably expect the sequence of Mach-reflections to join the sequence of the regular reflections at a point corresponding to the stationary Mach reflection. However, when we turn to weak shocks the situation becomes somewhat peculiar: The stationary limit of the sequence of Mach reflections and this does not join the sequence of the stable regular reflections. The question thus arises whether for the reflection of shock waves with $\zeta _{1,2}<2.26$ the 'unstable' reflections with angles of incidence $\alpha$ greater than $\alpha _{M}$ cannot after all be realized. We shall return to these questions after we have considered in $\S 3$ the general conditions for the existence of three shocks together with a vortex sheet to be in equilibrium.

3. The conditions for the Stationary Existence of Three Shocks

Fig. 6

Fig. 6

Consider a configuration of 3 shock waves (OB, OC, OE) and a vortex sheet (OD) as shown in Figure 6. We shall consider the phenomenon in a frame of reference in which the line of intersection of the shock waves and the vortex sheet is at rest. Finally, let OA define the direction of motion of the gas in region 1 in the frame of reference chosen.

Fig. 5

Fig. 5

Let the shock OB be of a given intensity $\zeta _{1,2}$. Then according to the Rankine-Hugoniot equations in the forms (1) and (2) the velocity of the gas in region 1 normal to the shock front OB in units of the velocity of sound in this region is given by equation (3) and accordingly

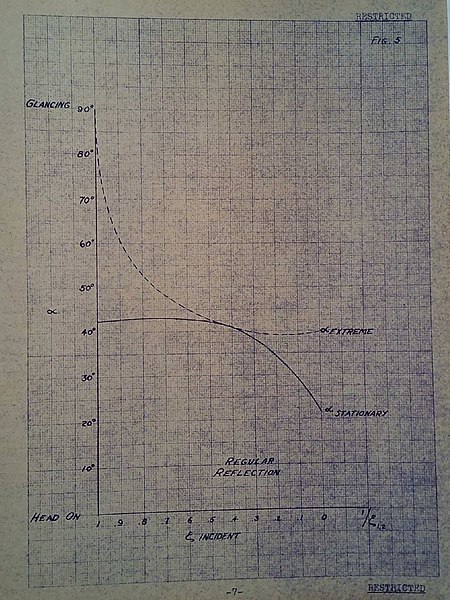
$\sigma _{\parallel }^{(1,2)}=\sigma _{\perp }^{(1,2)}\cot \alpha .$

(8)

The velocity of the gas in the region 2 both in magnitude and in direction can therefore be readily determined through the equations (1) and (2). For crossing the shock OC inclined at an angle $\beta$ to the direction of OB we can again use the Rankine-Hugoniot equations with

$\left.{\begin{array}{lll}\sigma _{\perp }^{(2,3)}&={\frac {1}{c_{2}}}\left(\tau _{\perp }^{(1,2)}\cos \beta +\sigma _{\parallel }^{(1,2)}\sin \beta \right)\\\sigma _{\parallel }^{(2,3)}&={\frac {1}{c_{2}}}\left(\tau _{\perp }^{(1,2)}\sin \beta -\sigma _{\parallel }^{(1,2)}\cos \beta \right).\end{array}}\right.$

(9)

Thus with the foregoing values for $\sigma _{\perp }$ and $\sigma _{\parallel }$ we can deduce the conditions behind OC. In particular we shall arrive in region 3 with a definite direction for the motion of the gas in this region. Moreover

$\zeta _{2,3}={\frac {P_{3}}{P_{2}}}={\frac {1}{\gamma +1}}\left\{2\gamma \left[\sigma _{\perp }^{(2,3)}\right]^{2}-(\gamma -1)\right\}.$

(10)

Now the shock OE must be so inclined to the direction of motion OA in region 1 that the pressure behind the shock OE is the same as in region 3. In other words the equation determining the angle Having determined $\gamma$ by this relation we can cross the shock (now of a known intensity) OB and arrive in region 4 with a definite direction for the motion of the gas. For an arbitrarily initially assigned value of $\beta$ the direction of motion derived for region 3 after crossing the two shocks OB and OC will not in general agree with that derived for region 4 after crossing the single shock OE. By trial and error we can adjust the angle $\beta$ till the directions of motion in the regions 3 and 4 agree.^[2] In this manner we can determine the direction of the vortex sheet which will be in equilibrium with a shock OB of given intensity and with a specified direction of motion in region 1.

The method described in the preceding paragraph is suitable for the purpose of isolating numerically configurations of three shocks in equilibrium, particularly if tables of solutions of the appropriate Rankine-Hugoniot equations are available. Tables of the Rankine-Hugoniot function for $\gamma =1.4$ are provided in the Appendix. Using these tables the three shock solutions depicted in Figs. 7, 8 and 9 were obtained.

4. Discussion of the Results of Figs. 7, 8 and 9.

Considering first the case of a strong incident shock we find that for $\zeta =7.0225$ (Fig.7) the stationary Mach reflection occurs for an angle of incidence $\alpha =31.25^{\circ }$. This angle is less than the angle at which regular reflection ceases for shocks of intensity, namely $42^{\circ }$. Moreover this stationary Mach reflection occurs when the reflected shock corresponds to a "stable" reflection. For increasing angles of incidence we get the three shock configurations of Fig. 7. It is to be particularly noticed that these solutions terminate for an angle of incidence $\alpha \sim 63^{\circ }$. At this angle the "Mach" shock becomes a continuation of the original shock, while the reflected shock and the vortex sheet disappear. We should, however, note in this connection that for an angle of incidence of $50^{\circ }$ the vortex sheet is inclined to the horizontal by about $20^{\circ }$. Consequently the non-satisfaction of the boundary condition on the reflecting surface in the region behind the Mach front will make the situation actually realized in practice to deviate considerably from those derived here on the basis of the stationary interaction of three shocks. On the other hand, for angles of incidence $\alpha$ which are only slightly greater than $\alpha _{M}$ the inclination of the vortex sheet to the horizontal is only very slight: accordingly under these circumstances the three shock solutions may be expected to represent on a first approximation the situations actually realized in the Mach effect.

In contrast to the relatively simple case presented by the strong shocks the weak shocks present a case which is more difficult to interpret. Thus considering the case of a relatively weak shock we find that for incident shocks of intensity $\zeta =1.111$ we have the sequence of three shock configurations depicted in Fig. 9. Here the stationary Mach reflection occurs for an angle of incidence $\alpha _{M}=42.5^{\circ }$. The corresponding angle of reflection is $85^{\circ }$. In other words the solution to the problem of regular reflection to which the present stationary Mach solution corresponds is the "unstable" one. So that from one point of view we may suppose that the stationary Mach reflection realized in this manner may not in fact occur in practice. On the other hand if we formally continue the three shock solutions beyond the angle $\alpha _{M}$ we are led to configurations of shocks which are in striking agreement with what have sometimes been observed in the photographs of shocks issuing from a bullet of the type shown in Fig. 10.

Fig. 10

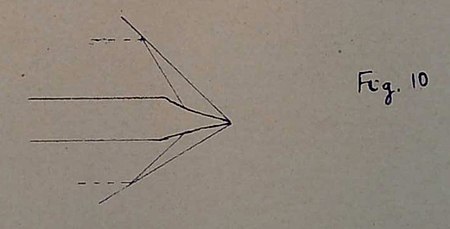
Fig. 10

On the strength of this evidence we are tempted to conclude that when two shocks (at least one of which is of weak intensity) intersect at a relatively small angle we would in fact be led to configurations of shocks and vortex sheet of the kind shown in Fig. 7 (see particularly the cases for $\alpha =50^{\circ }$ and $52.5^{\circ }$). We may therefore even expect that the stationary Mach reflection occurring on the "unstable" branch of the regular reflection may indeed be realized under suitable circumstances. If we should accept this, the question as to what happens when the angle of incidence of a relatively weak shock be gradually increased raises some peculiarly delicate considerations. Specifically, what may be expected to happen if a shock of intensity $\zeta =1.111$ be allowed to be incident on rigid surface at an angle of $47.5^{\circ }$. Will a stable reflection with $\alpha '\simeq 47.5^{\circ }$ or the unstable reflection with $\alpha '\simeq 84^{\circ }$ or a Mach effect with $\alpha '\simeq 96.5^{\circ }$ occur? The situation corresponding to the first and the last of the three alternatives enumerated can apparently be realized under suitable circumstances. This places the so called "unstable" reflections in a very peculiar position. It is not impossible that laboratory experiments may settle these questions more effectively than theoretical discussions.

Finally in Fig. * we have an intermediate case. Here we have considered three shock solutions for an incident shock with $\zeta =2$. For this case the stationary Mach reflection also occurs on the unstable branch of the regular reflection but in this case the two solutions for the reflection doe not differ very appreciably.

S. Chandrasekhar

Page:Threeshockwaves.pdf/12 Page:Threeshockwaves.pdf/13 Page:Threeshockwaves.pdf/14 Page:Threeshockwaves.pdf/15 Page:Threeshockwaves.pdf/16 Page:Threeshockwaves.pdf/17 Page:Threeshockwaves.pdf/18 Page:Threeshockwaves.pdf/19 Page:Threeshockwaves.pdf/20

APPENDIX

The Rankine-Hugoniot functions $(\gamma =1.4)$, namely Page:Threeshockwaves.pdf/22 Page:Threeshockwaves.pdf/23 Page:Threeshockwaves.pdf/24 Page:Threeshockwaves.pdf/25 Page:Threeshockwaves.pdf/26

1. We may note here that what von Neumann calls $\zeta '$ is our $\zeta _{2,3}$ while his $\zeta$ is our $1/\zeta _{1,2}$.
2. It is clear that after the adjustments have been made for the directions of motion in regions 3 and 4 to agree we shall still be left in general with a difference in the magnitude of velocity on either side of the common direction of motion; in other words, we have a vortex sheet in this region.