On the Determination of the Velocity of a Projectile from the Beat Waves Produced by Interference with the Waves of Modified Frequency Reflected from the Projectile
This page does not provide license information. Pages with no license information may be nominated for deletion. If you'd like to help, see Help:Copyright tags or comment. |
Ballistic Research
Laboratory Report No. 395
Chandrasekhar/mel
Aberdeen Proving Ground, Md.
31 August 1943
ON THE DETERMINATION OF THE VELOCITY OF A PROECJECTILE FROM THE BEAT WAVES PRODUCED BY INTERFERENCE WITH THE WAVES OF MODIFIED FREQUENCY REFLECTED FROM THE PROJECTILE
Abstract
In this report we examine as to what the basic information is which is provided by following a projectile in motion by radio waves of high frequency and using the beats produced by interference with the reflected waves of modified frequency. It is known that by counting the number of beat waves in a specified interval of time we are in principle able only to infer the position of the projectile at the end of the interval considered from a knowledge of its position at the beginning of the interval. On the basis of this fact, a practical method is outlined for determining the approximate velocities of the projectile along its trajectory.
1. A method has recently been developed by the Westinghouse Co. in collaboration with this laboratory in which the radio Doppler effect is used to determine the velocities and the drag coefficients for the various projectiles. The principle of this method is quite simple: We allow the micro waves of a given frequency emitted by a transmitter to be reflected from a projectile in motion. On account of the Doppler effect these reflected waves have frequencies slightly different from that of the incident waves (see equation [1] below). Consequently, if we now superpose the reflected wave trains on a wave train having the same frequency as the incident waves we shall obtain a beat phenomenon. It is evident that quantitative measures based on the existence of this beat phenomenon should enable us to determine the dynamical characteristics of the trajectory. It is the object of this report to analyse as to what can be inferred directly from a record of the "beat-wave" and indicate how the velocity of the projectile along its trajectory can be derived.
2. The wave train reflected from a moving projectile has the form
(1)
where is the incident frequency (with respect to a stationary observer) and
(2)
where denotes the velocity of light, the velocity of the projectile, and unit vectors in the directions pointing from the receiver, respectively, transmitter, to the instantaneous position of the projectile.
Let us first consider the result of combining the reflected wave train with an incident wave train of the form
(3)
The result will be a beat phenomenon which can be represented (apart from additive factors) by
(4)
If had been a constant then the constant beat frequency can be determined by counting the number of waves in a specified interval of time . For, then
(5)
However, in practice will be a function of time. This dependence of on time arises principally from the geometry of the situation which makes and vary with time during the intervals considered. To a lesser extent the variation of may also result from the variation of along the path of the projectile. The question now arises as to how best we can interpret the number of waves counted during a specified interval of time. As we shall see presently the obvious way of regarding as an "average" frequency does not provide the most satisfactory or indeed, even the most convenient one for the practical reduction of the observations.
3. Before proceeding further with the interpretation of when is a function of time we should perhaps remark that in order that the procedure may at all have an unambiguous meaning it is necessary that two conditions be satisfied. First that does not change appreciably during a time of the order and second that the interval be large compared to . We shall assume in our further discussions that these conditions are in fact satisfied. Accordingly we can subdivide the interval into a large number of subintervals such that each of these intervals are large compared to but small compared to . Under these circumstances, the number of waves counted during the interval can be written as
(6)
where denotes a value of included in the interval . One further remark should be made concerning equation (6) to avoid possible misunderstandings: During the interval must always remain of the same sign: otherwise the conditions we have stated will not be met. Hence, under the conditions of the problem equation (6) can be replaced by
(7)
Moreover, it is also clear that to a sufficient approximation we can replace the summation in the foregoing formula by an integral and obtain
(8)
Substituting for from equation (2) we finally have
(9)
4. We shall now consider the explicit evaluation of the formula established in 3.
Considering the first of the two integrals in equation (9), let the receiver be located on the -axis at a height (see Fig. 1) and let the path of the projectile be confined to -plane and further be represented by
(10)
Finally, let denote the position of the projectile at time .

Fig. 1
The direction cosines of the instantaneous line of sight are seen to be
(11)
while the direction cosines of the path of the projectile are Accordingly
(12)
Hence,
(13)
On the other hand, since
(14)
equation (13) becomes
(15)
We can express the result more simply as
(16)
where and are the distances of the projectile from the receiver at the beginning and at the end of the interval .
The second integral in equation (9) can be similarly evaluated. We have
(17)
where and are the distances of the projectile from the transmitter at the times and respectively.
Finally, combining equations (9), (16) and (17) we have
(18)
From this equation we see at once how the counted number of waves is directly related only to the positions of the projectiles at the beginning and at the end of the interval. Further this relation is exact.
According to equation (18), we can derive in a straightforward manner the position of the projectile at the end of any specified interval of time from a knowledge of the initial position of the projectile (i.e., and ), the geometry of the arrangement and the counted number of beats during the interval.
5. Now, in practice the number of beat waves in (4) are not directly counted. Instead, this beat wave is again combined with another wave train of the form
(19)
where is some constant frequency and which is very close to the frequencies ordinarily encountered. It is however necessary that in any given interval during which the beats are counted, does not change sign.
The superposition of the wave trains (4) and (19) will again result in a beat phenomenon which can be represented by a wave train of the form
(20)
The number of waves which will be counted in this wave train (20) in an interval will now be given by (cf. eq. [8])
(21)
or, since is a constant , we have
(22)
This equation can be expressed alternatively in the form
(23)
an equation which can be treated in exactly the same way as equation (18).
6. In view of our formula for the number of waves counted during a given interval of time, it appears that the most convenient arrangement for the purposes of the practical reduction of the observations is that indicated in Figure 2. Specifically, we arrange the receiver, the transmitter and the gun in such a way that the path of the projectile is confined to a plane which bisects the line joining the centers of the receiver and the transmitter orthogonally. For under these circumstances
(23)
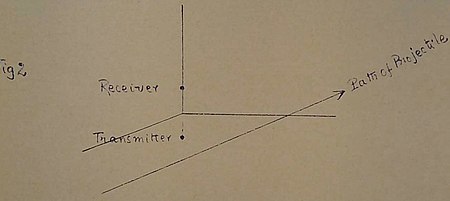
Fig. 2
for all points on the trajectory and equation (23) now reduces to
(24)
7. We have seen how the number of waves counted on a record of the beat phenomenon during a certain interval of time enables us to derive only the position of the projectile at the time from a knowledge of its position at the time . Since the position of the projectile at the instant of firing can be assumed known we should in principle be able to follow the projectile in its trajectory. This is precisely the basic information which is provided by the observations. It is to be particularly noted that in this statement as to what exactly the observations provide us we have had no occasion to take any reference to an "average" velocity. This may sound paradoxical since the Doppler principle utilized in the method is related to the velocity of the projectile during its motion. But the origin of the general belief that this method (based as it is on the Doppler principle) must be expected to yield velocities directly can be readily traced:
Suppose that the projectile is fired along the line joining the transmitter and the receiver. Then the counted number of waves during will give us . If it is now further supposed that the projectile moves with a constant velocity during the interval under consideration then . Accordingly in this case is directly related to . However, the situation in general is not as simple and as we have seen we can in principle derive only . The question now arises as to how from a knowledge of this quantity we can derive an average velocity for relatively small intervals .
Considering now for the sake of simplicity, the geometrical disposition of the apparatus as indicated in Fig. 2, the quantity directly deduced from the observations is
(25)
where we have used to denote the shortest distance from the mid point joining the centers of the receiver and the transmitter to the path of the projectile. We shall now suppose that is small compared to either or . Then, since
(26)
we have to a sufficient approximation
(27)
Setting
(28)
![{\displaystyle a\cos \left[2\pi (\nu _{o}+\delta \nu _{t})t+\varepsilon \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f51782f6fc7dd33e489b8c1acdb8c39e39dcc7)







![{\displaystyle a'\cos[2\pi \nu _{o}t+\varepsilon ']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e92e0f9793153f98ab7e1f600b3df3633c4285c)
![{\displaystyle A\cos[2\pi \delta \nu _{t}t+\varepsilon _{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4a1c6e5cada03d6f205a3737d0156267480963f)







































![{\displaystyle N={\frac {\nu _{o}}{c}}\left|\left[r_{2}^{\mathrm {(rec)} }+r_{2}^{\mathrm {(trans)} }-r_{1}^{\mathrm {(rec)} }-r_{1}^{\mathrm {(trans)} }\right]\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f9b4f801e6652203036e619ae328b5cd601352c)



![{\displaystyle C\cos \left[2\pi (\delta \nu _{o}-|\delta \nu _{t}|)t+\varepsilon _{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc8254e95ff3372c92dda89cb5f82ae7c745374)


![{\displaystyle N=\left|\left\{\delta \nu _{o}(t_{2}-t_{1})-{\frac {\nu _{o}}{c}}\left|\left[r_{2}^{\mathrm {(rec)} }+r_{2}^{\mathrm {(trans)} }-r_{1}^{\mathrm {(rec)} }-r_{1}^{\mathrm {(trans)} }\right]\right|\right\}\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc4c9318cd256f826e48fe70eb52c15f30b93)
![{\displaystyle N\pm \delta \nu _{o}(t_{2}-t_{1})={\frac {\nu _{o}}{c}}\left|\left[r_{2}^{\mathrm {(rec)} }+r_{2}^{\mathrm {(trans)} }-r_{1}^{\mathrm {(rec)} }-r_{1}^{\mathrm {(trans)} }\right]\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f81daeadc3eb44e7d9cdc1e3b9d97efe8321e58)

![{\displaystyle N\pm \delta \nu _{o}(t_{2}-t_{1})=2{\frac {\nu _{o}}{c}}|[r_{2}-r_{1}]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15fe0bde98042a1ba6641139cd592dc4a2044a78)



![{\displaystyle \left[r_{2}^{\mathrm {(rec)} }+r_{2}^{\mathrm {(trans)} }-r_{1}^{\mathrm {(rec)} }-r_{1}^{\mathrm {(trans)} }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2830bd406ef6731c9fc5cf043debd0811e6fa8)




![{\displaystyle \Delta r=(x_{2}-x_{1})\left[1-{\frac {r_{o}^{2}}{2x_{2}x_{1}}}+O(r_{o}^{4})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7469c22c612f830518258cad5338c27c01cfca)


