Optimum height for the bursting of a 105mm shell

by Subrahmanyan Chandrasekhar

BALLISTIC RESEARCH LABORATORY
MEMORANDUM REPORT NO. 139

SC/mo
Aberdeen Proving Ground, Md.
April 15, 1943

OPTIMUM HEIGHT FOR THE BURSTING OF A 105MM SHELL

 

1. The statement of the problem and its solution: It is required to find the height at which it is most advantageous to have a 105mm shell burst in order that the maximum injury may be inflicted on personnel.

It is found (as a result of the calculations to be presented) that the height at which it it most advantageous to have the shell burst is 75 feet.

2. Basis for the calculations: The experimental data on which the calculations were based are those of Mr. Tolch who has analyzed both the angular distribution of the fragments when a 105mm shell bursts and the distribution in weight of these fragments.

Regarding the angular distribution it appears that the greater proportion of the fragments in the lateral spray is confined to an annular cone with semi-angle of 7-1/2$^{\circ }$. We shall see later that the precise value of this semi-angle defining the angular width of the spray has no special influence on our results.

Optimum height for the bursting of a 105mm shell fig1

Regarding the distribution with mass of the fragments, Mr. Tolch's results can be relied upon for the heavier fragments ($m\gtrapprox 0.01\,\mathrm {lbs}$), while for the smaller fragments the reliability becomes steadily less on account of the necessary incompleteness in the recovery of these fragments. In order, therefore, to obtain a reasonable extrapolation of the distribution for the smaller masses, the total mass contributed by the fragments in the various mass groups was plotted against the mass of the fragment and from a smooth curve drawn through these points, a distribution was derived which formed the basis of further calculations. The observed and the derived distributions are compared in Table I. From this table, Table II giving the number of fragments in the downward lateral spray with masses greater than a given value was derived.

TABLE I

Distribution with Mass of the Fragments

m in lbs.	Observed	Derived
0.005	250	484
0.007		340
0.009	200	260
0.015	146	146
0.025	79	80
0.035	51	52
0.045	45	36
0.055	27	27
0.065	16	20
0.075	10	16
0.085	9	13
0.095	8	11
0.105	13	9
0.115	23	8
0.125		6
0.135		6
0.145		5
0.155		4
0.165		3
0.175		2
0.185		1

 

TABLE II

Number of fragments in the downward lateral spray with masses greater than m

 

m	$\int _{m}^{\infty }N(m)\,dm$
0.003	1176
0.005	765
0.007	523
0.009	353
0.015	223
0.025	150
0.035	110
0.045	88
0.055	66
0.065	52
0.075	42
0.085	34
0.095	27
0.105	22
0.115	18
0.125	13
0.135	10
0.145	7
0.155	5
0.165	3

3. The effectiveness and the ranges of the fragments of different masses: Another factor which it is necessary to decide on before we can estimate the height at which it it most advantageous to have the shell burst is concerned with the range and the effectiveness of a fragment of a given mass.

We shall suppose that a fragment is effective if it has a sufficient velocity to penetrate an inch of wood. Using a formula due to Welch (who has experimented on the penetration of wood by fragments of various masses) we find that a fragment of mass $m$ (in lbs.) will be effective if it has a velocity greater than $v_{*}(m)$ where

(1)$v_{*}(m)=210\,m^{-1/3}$

where $m$ is expressed in lbs. and $v$ in ft/sec.

Now the velocity with which the fragments are shot off from a 105mm shell is of the order of 3500 ft/sec. Consequently, a fragment of this shell which has a given mass $m$ will be effective only if it has traversed a range less than a certain value $r(m).$ To determine this maximum range as a function of the mass of the fragment the following formulae (again based on Welch) were used:

$r(m)=s_{1},\,\,v_{*}(m)=3500\,\,e^{-s_{1}/776\,m^{1/3}},$(2)

${\text{if}}\,\,v_{*}(m)\geq 1100\,\,$

and

$r(m)=s_{1}+s_{2},\,\,$(3)

$v_{*}(m)=3500\,\,e^{-(s_{1}+s_{2}/3)/776\,m^{1/3}},\,\,$

$1100=3500\,\,e^{-s_{1}/776\,m^{1/3}}\,\,{\text{if}}\,\,v_{*}(m)<1100.$

Using the foregoing formulae the following table was derived.

TABLE III

The Maximum Range for the Effectiveness of Fragments of Various Masses

m in lbs.	range in ft.	m in lbs.	range in ft.
0.0005	17	0.025	551
0.001	40	0.030	630
0.002	73	0.040	769
0.004	119	0.050	895
0.006	156	0.060	1006
0.008	209	0.080	1202
0.010	253	0.100	1376
0.015	368	0.200	2046
0.020	466	0.400	2801

 

In deriving Table III, we have, as we have already stated, used the British results on the retardation in air and the penetration into wood of fragments. However, it is now held that Welch's formula underestimates (possibly by a factor $2/3$) the retardation in air. On the other hand it appears that using Welch's results both for the penetration in air and in wood we are led to consistent results. Thus Inglis using a different criterion for effectiveness (namely that a fragment to be effective must have 150 ft. lbs. of energy) and using a retardation factor in air which is two thirds of Welch's finds ranges of the order of 70, 110 and 280 ft. for masses 0.0023, 0.0040 and 0.0095 lbs., respectively. These ranges of Inglis should be compared with the values we have derived namely 80, 120 and 250 ft., respectively. The agreement is satisfactory.

4. The estimate of the optimum height. The estimate of the optimum height was made on the basis of the following model.

Optimum height for the bursting of a 105mm shell fig 2

Let the shell explode at a height $h$ from the ground. We shall suppose further the lateral spray is symmetrical with respect to the $yz$ plane. Then the surface density of the fragments which arrive at the point $(x,y)$ and which are effective is given by

(4)$\rho (x,y)={\frac {1}{4\theta }}\int _{m_{*}}^{\infty }N(m)\,dm\,\,\cdot {\frac {h}{(h^{2}+x^{2}+y^{2})^{3/2}}},$

where $\theta$ (expressed in radians) is half the angular width of the spray and $m_{*}$ the smallest mass which arrives at $(x,y)$ and which is still effective i.e., $m_{*}$ is the mass which has the maximum effective range equal to $(h^{2}+x^{2}+y^{2})^{1/2}$.

Now let $A$ denote the effective area of a target. Then the area on the ground sprayed by fragments can be divided, in general, into two regions: An inner region I in which $\rho$ is greater than $A^{-1}$ and an outer region II in which $\rho$ is less than $A^{-1}$. Under these circumstances it is clear that in region I where $\rho \geq A^{-1}$ we are super effective in the sense that the entire personnel in this region may be expected to be seriously affected. In the other region the probability of hitting a particular target is proportional to $\rho$. Thus the number of casualties is given by

(5)$N=EA\sigma$

where $\sigma$ denotes the number of targets per unit area and

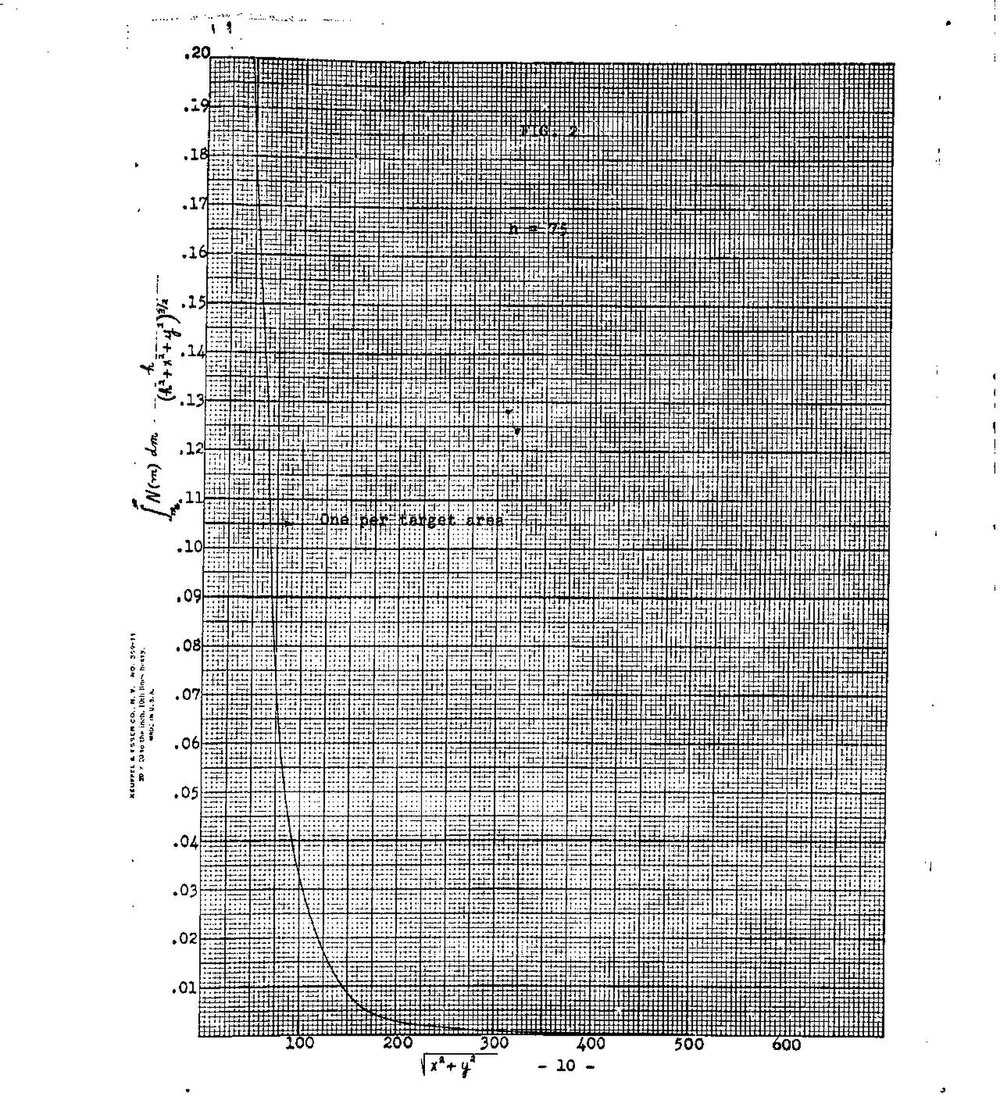
(6)$E=A^{-1}\iint _{\mathrm {region} \,I}dxdy+\iint _{\mathrm {region} \,II}\rho (x,y)\,dxdy.$

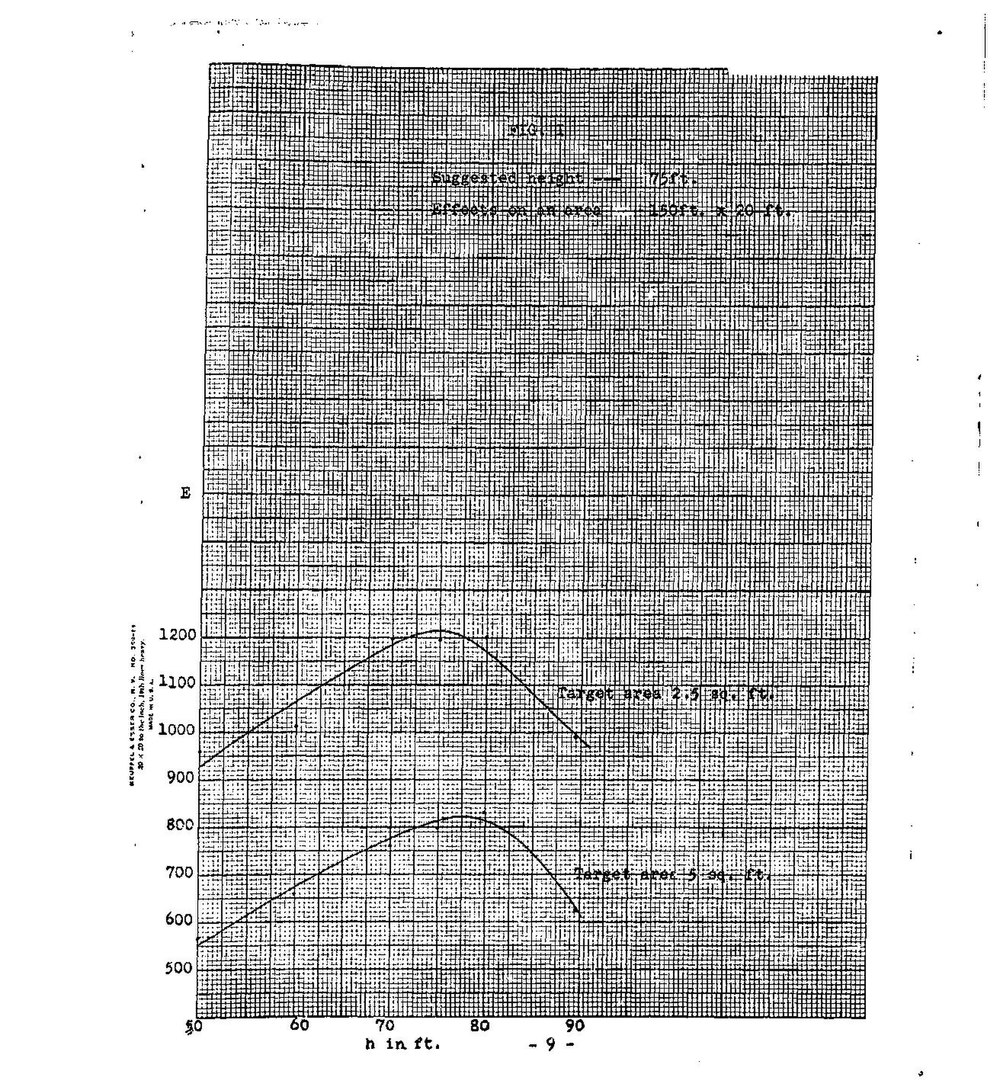
In Table IV the density (apart from the factor $1/4\theta$) is tabulated for various values of $h$. Finally the values of $E$ derived on the basis of the results of Table IV are plotted in Fig. 1. It is seen that within the uncertainties of the problem the optimum height is about 75 ft. for a wide range of target areas.

TABLE IV

$\int _{m_{*}}^{\infty }{\frac {N(m)h}{r^{3}}}\,dm\qquad r=(h^{2}+x^{2}+y^{2})^{1/2}$

$(x^{2}+y^{2})^{1/2}$	h=50	h=60	h=70	h=75	h=80	h=90	h=120
25	-	-	-	-	-	0.1380	0.0586
50	-	-	-	-	-	0.0955	0.0459
75	-	0.0874	0.0745	0.0722	0.0673	0.0559	0.0318
100	0.0376	0.0378	0.0338	0.0334	0.0324	0.0330	0.0189
125	0.0166	0.0169	0.0176	0.0174	0.0176	0.0168	0.0127
150	0.0076	0.0084	0.0089	0.0091	0.0093	0.0089	0.0079
175	0.0041	0.0047	0.0051	0.0050	0.0052	0.0052	0.0050
200	0.0023	0.0027	0.0029	0.0030	0.0030	0.0031	0.0033
250	0.0010	0.0011	0.0013	0.0014	0.0014	0.0015	0.0017
300	0.00049	0.00057	0.00065	0.00069	0.00072	0.00078	0.00092
400	0.00016	0.00018	0.00021	0.00022	0.00024	0.00026	0.00033
500	0.00007	0.00008	0.00009	0.00010	0.00010	0.00011	0.00014
600	0.00003	0.00004	0.00004	0.00005	0.00005	0.00005	0.00007
700	0.00002	0.00002	0.00002	0.00002	0.00003	0.00003	0.00004
800	0.00001	0.00001	0.00001	0.00001	0.00001	0.00002	0.00002

5. Some General Remarks: We have seen that the height at which it is most advantageous to have a 105mm shell burst is about 75 ft. for wide limits in the effective area of the target involved. The reason for this rough independence can be understood in terms of the following considerations:

Essentially the existence of an optimum height for burst depends on the extent to which the area on the ground where we are super-efficient (region I of §4) can be reduced. It cannot however be concluded that the optimum height corresponds to reducing this area to zero. For the fragments which are most numerous are those with small masses and these have ranges of the order of $h$ itself. Thus, when $h=75$, the fragments which are effective (i.e., with velocities greater than $v_{*}$ [Cf. eq. 1]) and which arrive on the ground directly below the point of burst must have masses greater than 0.0021 lb. (cf. Table III). Fragments with $m$ in this neighborhood are the most numerous, but their effect is confined to a very small area. Accordingly we must go to somewhat larger masses (with correspondingly longer ranges) to be really efficient. In other words, at the optimum height we must necessarily be super efficient in the regions directly below the point of burst. In other words the area over which we are super efficient must be reduced as much as is compatible with the circumstances of the problem.

The considerations of the preceding paragraph account also for relative insensitiveness of the optimum height with the target area within limits. For while a reduction in the effective target area requires a greater surface density of fragments this can be achieved by even a slight reduction in $h$ since by so doing we bring into range the smaller fragments which increase in number very rapidly with decreasing mass.

Again, it it clear that since a change in the half angle $\theta$ of the spray can be formally incorporated into the calculations as a change in target area, the optimum height is relatively insensitive also to changes in $\theta$. For a given total number of fragments, the surface density varies inversely as $\theta$. Hence, other things being equal a change in $\theta$ alters the surface densities by a constant factor and the final efficiency will be clearly the same if $\theta$ were kept unaltered but the target area increased by the same factor.

In our calculations we have assumed that the spray is symmetrical with respect to the $yz$ plane. A tilt of this spray with the vertical by a small angle $\phi$ can be taken into account by using for the optimum height the value

$75\,\cos \phi \qquad (\phi$ the angle of tilt of the spray with the vertical).

Considering all the uncertainties of the problem we may suggest as the optimum height for burst a value of 75 ft. In doubtful cases it might be safer to go down to as much as 70 ft. and in any event greater heights should be avoided as far as possible.

We may finally remark that if the shell bursts at 75 ft above the ground, the area which is effectively sprayed by the fragments is

$160\,{\text{ft by}}\,20\,{\text{ft}}\qquad ({\text{target area}}=5\,{\text{sq ft}})$

and

$130\,{\text{ft by}}\,20\,{\text{ft}}\qquad ({\text{target area}}=2-1/2\,{\text{sq ft}})$

Accordingly, when firing, it would be advantageous to have the shells burst at about 150 ft apart sideways and 20 ft. apart depth-wise (See Fig. 2)

Summary

This paper is devoted to determining the height at which it is most advantageous to have 105mm shell burst in order that the maximum injury may be inflicted on personnel. On the basis of the experimental data of Tolch on the fragmentation of the 105mm shell it is concluded that the optimum height is about 75 ft. Also when the shell does burst at this height, it effectively covers an area of 150 ft by 20 ft.

S. Chandrasekhar

Fig. 1

Fig. 2

COMMENTS ON THE RELATION OF THE PRECEDING REPORT TO RECENT OBSERVATIONS AT FORT BRAGG.

Recent experiments on the effect of ricochet and time fire of 105mm H.E. Shells against personnel, conducted by the Field Artillery Board at Fort Bragg, indicate an optimum altitude of burst as 45 feet instead of the 75 feet suggested by the computations of Dr. Chandrasekhar. This brings up the question of the reason for this experimental discrepancy.

The main reason appears to be that the computations of Dr. Chandrasekhar were presumably based on a tacit assumption of more deeply entrenched personnel, protected against fragments coming in at oblique angles, whereas the dummies used in the experiments at Fort Bragg came to within a few inches of the surface. This assumption would affect the computed optimum altitude of burst in two ways. First, obviously a very low burst could only injure personnel in a very small area. Thus whereas in the experiments at Fort Bragg, a burst at an altitude of 15-30 feet is found effective over a rather wide area, deeply entrenched horizontal personnel would be exposed to such a burst over a region perhaps 8 feet in diameter. And also, oblique hits have longer trajectories, and hence less striking velocity. This would explain the apparent decrease in striking velocity of small fragments from altitudes above 40 feet observed at Fort Bragg. It is usually supposed that this deceleration becomes important only for ranges of 70-100 feet; these would be consistent for fragments travelling obliquely at angles of 30°-45° with the horizontal.

Thus Dr. Chandrasekhar's conclusions should apply to entrenched personnel, screened against oblique hits.

Garrett Birkhoff