APPENDIX III.
Proof that, if any one Proposition of Table II be granted as an Axiom, the rest can be deduced from it. (See pp. 34, 40.)
"… and so we make it quite a merry-go-rounder." I was obliged to consider a little before I understood what Mr. Peggotty meant by this figure, expressive of a complete circle of intelligence.
It is to be proved that, if any one of the Propositions of Table II be granted, the rest can be proved.
It is assumed that the lesser of two unequal finite magnitudes of the same kind may be multiplied so as to exceed the greater.
Euclid I, 1 to 28, is assumed as proved.
It is assumed that, where two Propositions are Contranominals, so that each can be proved from the other, it is not necessary to include both in the series of proofs.
Lemma 1.
A Pair of Lines, of which one contains two points equidistant from the other, have a common perpendicular.
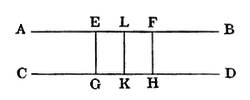
Let AB contain 2 points E, F, equidistant from CD. From E, F, draw EG, FH, ⊥ CD; bisect GH in K, and EF in L, and join KL.
