is also , as we see by considering the introduction (through a fine tube) of one body into the interior of the other. A comparison with another method of generating the interface, similar to that previously employed when but one body was in question, will now allow us to evaluate .
The work required to cleave asunder the parts of the first fluid which lie on the two sides of an ideal plane passing through the interior, is per unit of area , and the free surface produced is two units in area. So for the second fluid the corresponding work is . This having been effected, let us now suppose that each of the units of area of free surface of fluid (1) is allowed to approach normally a unit area of (2) until contact is established. In this process work is gained which we may denote by for each pair. On the whole, then, the work expended in producing two units of interface is , and this, as we have seen, may be equated to . Hence
| (47) |
If the two bodies are similar,
and , as it should do.
Laplace does not treat systematically the question of interfacial tension, but he gives incidentally in terms of his quantity H a relation analogous to (47).
If , would be negative, so that the interface would of itself tend to increase. In this case the fluids must mix. Conversely, if two fluids mix, it would seem that must exceed the mean of and ; otherwise work would have to be expended to effect a close alternate stratification of the two bodies, such as we may suppose to constitute a first step in the process of mixture (Dupré, Théorie mécanique de la chaleur, p. 372; Kelvin, Popular Lectures, p. 53).
The value of has already been calculated (32). We may write
| (48) |
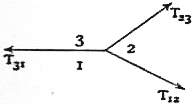
and in general the functions , or , must be regarded as capable of assuming different forms. Under these circumstances there is no limitation upon the values of the interfacial tensions for three fluids, which we may denote by , , . If the three fluids can remain in contact with one another, the sum of any two of the quantities must exceed the third, and by Neumann’s rule the directions of the interfaces at the common edge must be parallel to the sides of a triangle, taken proportional to , , . If the above-mentioned condition be not satisfied, the triangle is imaginary, and the three fluids cannot rest in contact, the two weaker tensions, even if acting in full concert, being incapable of balancing the strongest. For instance, if , the second fluid spreads itself indefinitely upon the interface of the first and third fluids.
The experimenters who have dealt with this question, C. G. M. Marangoni, van der Mensbrugghe, Quincke, have all arrived at results inconsistent with the reality of Neumann’s triangle. Thus Marangoni says (Pogg. Annalen, cxliii. p. 348, 1871):—“Die gemeinschaftliche Oberfläche zweier Flüssigkeiten hat eine geringere Oberflächenspannung als die Differenz der Oberflächenspannung der Flüssigkeiten selbst (mit Ausnahme des Quecksilbers).” Three pure bodies (of which one may be air) cannot accordingly remain in contact. If a drop of oil stands in lenticular form upon a surface of water, it is because the water-surface is already contaminated with a greasy film.
On the theoretical side the question is open until we introduce some limitation upon the generality of the functions. By far the simplest supposition open to us is that the functions are the same in all cases, the attractions differing merely by coefficients analogous to densities in the theory of gravitation. This hypothesis was suggested by Laplace, and may conveniently be named after him. It was also tacitly adopted by Young, in connexion with the still more special hypothesis which Young probably had in view, namely that the force in each case was constant within a limited range, the same in all cases, and vanished outside that range.
As an immediate consequence of this hypothesis we have from (28)
| (49) |
| (50) |
where , are the same for all bodies.
But the most interesting results are those which Young (Works, vol. i. p. 463) deduced relative to the interfacial tensions of three bodies. By (37), (48),
| (51) |
so that by (47), (50),
| (52) |
According to (52), the interfacial tension between any two bodies is proportional to the square of the difference of their densities. The densities , , being in descending order of magnitude, we may write
so that necessarily exceeds the sum of the other two interfacial tensions. We are thus led to the important conclusion that according to this hypothesis Neumann’s triangle is necessarily imaginary, that one of three fluids will always spread upon the interface of the other two.
Another point of importance may be easily illustrated by this theory, viz. the dependency of capillarity upon abruptness of transition. “The reason why the capillary force should disappear when the transition between two liquids is sufficiently gradual will now be evident. Suppose that the transition from to is made in two equal steps, the thickness of the intermediate layer of density being large compared to the range of the molecular forces, but small in comparison with the radius of curvature. At each step the difference of capillary pressure is only one-quarter of that due to the sudden transition from to , and thus altogether half the effect is lost by the interposition of the layer. If there were three equal steps, the effect would be reduced to one-third, and so on. When the number of steps is infinite, the capillary pressure disappears altogether.” (“Laplace’s Theory of Capillarity,” Rayleigh, Phil. Mag., 1883, p. 315.)
According to Laplace’s hypothesis the whole energy of any number of contiguous strata of liquids is least when they are arranged in order of density, so that this is the disposition favoured by the attractive forces. The problem is to make the sum of the interfacial tensions a minimum, each tension being proportional to the square of the difference of densities of the two contiguous liquids in question. If the order of stratification differ from that of densities, we can show that each step of approximation to this order lowers the sum of tensions. To this end consider the effect of the abolition of a stratum , contiguous to and . Before the change we have , and afterwards (. The second minus the first, or the increase in the sum of tensions, is thus
Hence, if be intermediate in magnitude between and , the sum of tensions is increased by the abolition of the stratum; but, if be not intermediate, the sum is decreased. We see, then, that the removal of a stratum from between neighbours where it is out of order and its introduction between neighbours where it will be in order is doubly favourable to the reduction of the sum of tensions; and since by a succession of such steps we may arrive at the order of magnitude throughout, we conclude that this is the disposition of minimum tensions and energy.
So far the results of Laplace’s hypothesis are in marked accordance with experiment; but if we follow it out further, discordances begin to manifest themselves. According to (52)
| (53) |
a relation not verified by experiment. What is more, (52) shows that according to the hypothesis is necessarily positive;