where h is the difference of level of the head and tail water, and may be termed the effective head producing flow.
 |
| Fig. 42. |
Case where the Pressures are different on the Free Surface and at the Orifice.—Let the fluid flow from a vessel in which the pressure is p0 into a vessel in which the pressure is p, fig. 42. The pressure p0 will produce the same effect as a layer of fluid of thickness p0/G added to the head water; and the pressure p, will produce the same effect as a layer of thickness p/G added to the tail water. Hence the effective difference of level, or effective head producing flow, will be
and the velocity of discharge will be
We may express this result by saying that differences of pressure at the free surface and at the orifice are to be reckoned as part of the effective head.
Hence in all cases thus far treated the velocity of the jet is the velocity due to the effective head, and the discharge, allowing for contraction of the jet, is
where ω is the area of the orifice, cω the area of the contracted section of the jet, and h the effective head measured to the centre of the orifice. If h and ω are taken in feet, Q is in cubic feet per second.
It is obvious, however, that this formula assumes that all the filaments have sensibly the same velocity. That will be true for horizontal orifices, and very approximately true in other cases, if the dimensions of the orifice are not large compared with the head h. In large orifices in say a vertical surface, the value of h is different for different filaments, and then the velocity of different filaments is not sensibly the same.
Simple Orifices—Head Constant
 |
| Fig. 43. |
§ 39. Large Rectangular Jets from Orifices in Vertical Plane Surfaces.—Let an orifice in a vertical plane surface be so formed that it produces a jet having a rectangular contracted section with vertical and horizontal sides. Let b (fig. 43) be the breadth of the jet, h1 and h2 the depths below the free surface of its upper and lower surfaces. Consider a lamina of the jet between the depths h and h + dh. Its normal section is bdh, and the velocity of discharge √2gh. The discharge per second in this lamina is therefore b√2gh dh, and that of the whole jet is therefore
where the first factor on the right is a coefficient depending on the form of the orifice.
Now an orifice producing a rectangular jet must itself be very approximately rectangular. Let B be the breadth, H1, H2, the depths to the upper and lower edges of the orifice. Put
Then the discharge, in terms of the dimensions of the orifice, instead of those of the jet, is
the formula commonly given for the discharge of rectangular orifices. The coefficient c is not, however, simply the coefficient of contraction, the value of which is
and not that given in (7). It cannot be assumed, therefore, that c in equation (8) is constant, and in fact it is found to vary for different values of B/H2 and B/H1, and must be ascertained experimentally.
Relation between the Expressions (5) and (8).—For a rectangular orifice the area of the orifice is ω = B(H2 − H1), and the depth measured to its centre is 12 (H2 + H1). Putting these values in (5),
From (8) the discharge is
Hence, for the same value of c in the two cases,
Let H1/H2 = σ, then
If H1 varies from 0 to ∞, σ( = H1/H2) varies from 0 to 1. The following table gives values of the two estimates of the discharge for different values of σ:—
| H1/H2 = σ. | Q2/Q1. | H1/H2 = σ. | Q2/Q1. |
| 0.0 | .943 | 0.8 | .999 |
| 0.2 | .979 | 0.9 | .999 |
| 0.5 | .995 | 1.0 | 1.000 |
| 0.7 | .998 |
Hence it is obvious that, except for very small values of σ, the simpler equation (5) gives values sensibly identical with those of (8). When σ < 0.5 it is better to use equation (8) with values of c determined experimentally for the particular proportions of orifice which are in question.
 |
| Fig. 44. |
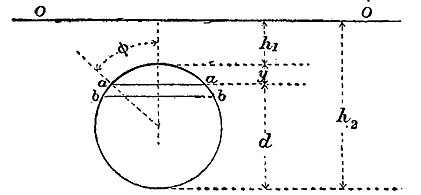
§ 40. Large Jets having a Circular Section from Orifices in a Vertical Plane Surface.—Let fig. 44 represent the section of the jet, OO being the free surface level in the reservoir. The discharge through the horizontal strip aabb, of breadth aa = b, between the depths h1 + y and h1 + y + dy, is
The whole discharge of the jet is
But b = d sin φ; y = 12d (1 − cos φ); dy = 12d sin φ dφ. Let ε = d/(2h1 + d), then
From eq. (5), putting ω = πd 2/4, h = h1 + d/2, c = 1 when d is the diameter of the jet and not that of the orifice,
For
and for
So that in this case also the difference between the simple formula (5) and the formula above, in which the variation of head at different parts of the orifice is taken into account, is very small.
Notches and Weirs
§ 41. Notches, Weirs and Byewashes.—A notch is an orifice extending up to the free surface level in the reservoir from which the discharge takes place. A weir is a structure over which the water flows, the discharge being in the same conditions as for a notch. The formula of discharge for an orifice of this kind is ordinarily deduced by putting H1 = 0 in the formula for the corresponding orifice, obtained as in the preceding section. Thus for a rectangular notch, put H1 = 0 in (8). Then
where H is put for the depth to the crest of the weir or the bottom of the notch. Fig. 45 shows the mode in which the discharge occurs in the case of a rectangular notch or weir with a level crest. As, the free surface level falls very sensibly near the notch, the head H should be measured at some distance back from the notch, at a point where the velocity of the water is very small.
Since the area of the notch opening is BH, the above formula is of the form
where k is a factor depending on the form of the notch and expressing the ratio of the mean velocity of discharge to the velocity due to the depth H.
§ 42. Francis’s Formula for Rectangular Notches.—The jet discharged through a rectangular notch has a section smaller than BH, (a) because of the fall of the water surface from the point where H




