to flow away down the original stream channel, or is stored in separate reservoirs and used as compensation water. To accomplish the separation of the flood and ordinary water, advantage is taken of the different horizontal range of the parabolic path of the water falling over a weir, as the depth on the weir and, consequently, the velocity change. Fig. 55 shows one of these separating weirs in the form in which they were first introduced on the Manchester Waterworks; fig. 56 a more modern weir of the same kind designed by Sir A. Binnie for the Bradford Waterworks. When the quantity of water coming down the stream is not excessive, it drops over the weir into a transverse channel leading to the reservoirs. In flood, the water springs over the mouth of this channel and is led into a waste channel.
 |
| Fig. 56. |
It may be assumed, probably with accuracy enough for practical purposes, that the particles describe the parabolas due to the mean velocity of the water passing over the weir, that is, to a velocity
where h is the head above the crest of the weir.
Let cb = x be the width of the orifice and ac = y the difference of level of its edges (fig. 57). Then, if a particle passes from a to b in t seconds,
which gives the width x for any given difference of level y and head h, which the jet will just pass over the orifice. Set off ad vertically and equal to 12g on any scale; af horizontally and equal to 23 √(gh). Divide af, fe into an equal number of equal parts. Join a with the divisions on ef. The intersections of these lines with verticals from the divisions on af give the parabolic path of the jet.
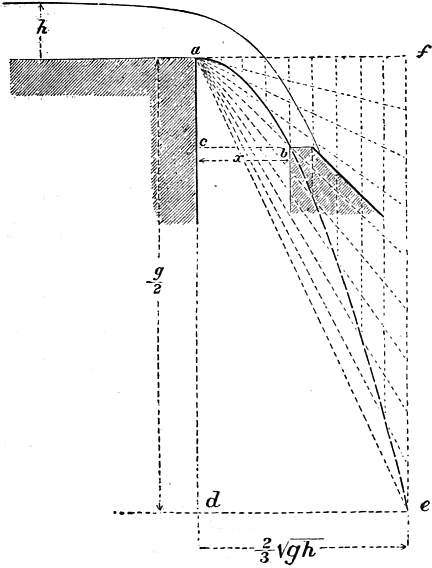 |
| Fig. 57. |
Mouthpieces—Head Constant
§ 49. Cylindrical Mouthpieces.—When water issues from a short cylindrical pipe or mouthpiece of a length at least equal to 112 times its smallest transverse dimension, the stream, after contraction within the mouthpiece, expands to fill it and issues full bore, or without contraction, at the point of discharge. The discharge is found to be about one-third greater than that from a simple orifice of the same size. On the other hand, the energy of the fluid per unit of weight is less than that of the stream from a simple orifice with the same head, because part of the energy is wasted in eddies produced at the point where the stream expands to fill the mouthpiece, the action being something like that which occurs at an abrupt change of section.
Let fig. 58 represent a vessel discharging through a cylindrical mouthpiece at the depth h from the free surface, and let the axis of the jet XX be taken as the datum with reference to which the head is estimated. Let Ω be the area of the mouthpiece, ω the area of the stream at the contracted section EF. Let v, p be the velocity and pressure at EF, and v1, p1 the same quantities at GH. If the discharge is into the air, p1 is equal to the atmospheric pressure pa.
The total head of any filament which goes to form the jet, taken at a point where its velocity is sensibly zero, is h + pa/G; at EF the total head is v2/2g + p/G; at GH it is v12/2g + p1/G.
Between EF and GH there is a loss of head due to abrupt change of velocity, which from eq. (3), § 36, may have the value
Adding this head lost to the head at GH, before equating it to the heads at EF and at the point where the filaments start into motion,—
But ωv = Ωv1, and ω = ccΩ, if cc is the coefficient of contraction within the mouthpiece. Hence
Supposing the discharge into the air, so that p1 = pa,
 |
| Fig. 58. |
where the coefficient on the right is evidently the coefficient of velocity for the cylindrical mouthpiece in terms of the coefficient of contraction at EF. Let cc = 0.64, the value for simple orifices, then the coefficient of velocity is
The actual value of cv, found by experiment is 0.82, which does not differ more from the theoretical value than might be expected if the friction of the mouthpiece is allowed for. Hence, for mouthpieces of this kind, and for the section at GH,
It is easy to see from the equations that the pressure p at EF is less than atmospheric pressure. Eliminating v1, we get
or
If a pipe connected with a reservoir on a lower level is introduced into the mouthpiece at the part where the contraction is formed (fig. 59), the water will rise in this pipe to a height
If the distance X is less than this, the water from the lower reservoir will be forced continuously into the jet by the atmospheric pressure, and discharged with it. This is the crudest form of a kind of pump known as the jet pump.
§ 50. Convergent Mouthpieces.—With convergent mouthpieces there is a contraction within the mouthpiece causing a loss of head, and a diminution of the velocity of discharge, as with cylindrical mouthpieces. There is also a second contraction of the stream outside the mouthpiece. Hence the discharge is given by an equation of the form
where Ω is the area of the external end of the mouthpiece, and ccΩ the section of the contracted jet beyond the mouthpiece.
Convergent Mouthpieces (Castel’s Experiments).—Smallest diameter of
orifice = 0.05085 ft. Length of mouthpiece = 2.6 Diameters.
| Angle of Convergence. | Coefficient of Contraction, cc | Coefficient of Velocity, cv | Coefficient of Discharge, c |
| 0° 0′ | .999 | .830 | .829 |
| 1° 36′ | 1.000 | .866 | .866 |
| 3° 10′ | 1.001 | .894 | .895 |
| 4° 10′ | 1.002 | .910 | .912 |
| 5° 26′ | 1.004 | .920 | .924 |
| 7° 52′ | .998 | .931 | .929 |
| 8° 58′ | .992 | .942 | .934 |
| 10° 20′ | .987 | .950 | .938 |
| 12° 4′ | .986 | .955 | .942 |
| 13° 24′ | .983 | .962 | .946 |
| 14° 28′ | .979 | .966 | .941 |
| 16° 36′ | .969 | .971 | .938 |
| 19° 28′ | .953 | .970 | .924 |
| 21° 0′ | .945 | .971 | .918 |
| 23° 0′ | .937 | .974 | .913 |
| 29° 58′ | .919 | .975 | .896 |
| 40° 20′ | .887 | .980 | .869 |
| 48° 50′ | .861 | .984 | .847 |
The maximum coefficient of discharge is that for a mouthpiece with a convergence of 13°24′.
