angular velocities of a pair of connected circular pulleys or drums are inversely as the effective radii.
A crossed belt, as in fig. 108, A, reverses the direction of the rotation communicated; an uncrossed belt, as in fig. 108, B, preserves that direction.
The length L of an endless belt connecting a pair of pulleys whose effective radii are r1, r2, with parallel axes whose distance apart is c, is given by the following formulae, in each of which the first term, containing the radical, expresses the length of the straight parts of the belt, and the remainder of the formula the length of the curved parts.
For a crossed belt:—
| L = 2 √{c2 − (r1 + r2)2} + (r1 + r2) π − 2 sin−1 | r1 + r2 | ; |
| c |
and for an uncrossed belt:—
| L = 2 √{c2 − (r1 − r2)2 } + π (r1 + r2 + 2 (r1 − r2) sin−1 | r1 − r2 | ; |
| c |
in which r1 is the greater radius, and r2 the less.
When the axes of a pair of pulleys are not parallel, the pulleys should be so placed that the part of the belt which is approaching each pulley shall be in the plane of the pulley.
§ 60. Speed-Cones.—A pair of speed-cones (fig. 109) is a contrivance for varying and adjusting the velocity ratio communicated between a pair of parallel shafts by means of a belt. The speed-cones are either continuous cones or conoids, as A, B, whose velocity ratio can be varied gradually while they are in motion by shifting the belt, or sets of pulleys whose radii vary by steps, as C, D, in which case the velocity ratio can be changed by shifting the belt from one pair of pulleys to another.
 |
| Fig. 109. |
In order that the belt may fit accurately in every possible position on a pair of speed-cones, the quantity L must be constant, in equations (32 A) or (32 B), according as the belt is crossed or uncrossed.
For a crossed belt, as in A and C, fig. 109, L depends solely on c and on r1 + r2. Now c is constant because the axes are parallel; therefore the sum of the radii of the pitch-circles connected in every position of the belt is to be constant. That condition is fulfilled by a pair of continuous cones generated by the revolution of two straight lines inclined opposite ways to their respective axes at equal angles.
For an uncrossed belt, the quantity L in equation (32 B) is to be made constant. The exact fulfilment of this condition requires the solution of a transcendental equation; but it may be fulfilled with accuracy sufficient for practical purposes by using, instead of (32 B) the following approximate equation:—
The following is the most convenient practical rule for the application of this equation:—
Let the speed-cones be equal and similar conoids, as in B, fig. 109, but with their large and small ends turned opposite ways. Let r1 be the radius of the large end of each, r2 that of the small end, r0 that of the middle; and let v be the sagitta, measured perpendicular to the axes, of the arc by whose revolution each of the conoids is generated, or, in other words, the bulging of the conoids in the middle of their length. Then
2π = 6.2832; but 6 may be used in most practical cases without sensible error.
The radii at the middle and end being thus determined, make the generating curve an arc either of a circle or of a parabola.
§ 61. Linkwork in General.—The pieces which are connected by linkwork, if they rotate or oscillate, are usually called cranks, beams and levers. The link by which they are connected is a rigid rod or bar, which may be straight or of any other figure; the straight figure being the most favourable to strength, is always used when there is no special reason to the contrary. The link is known by various names in various circumstances, such as coupling-rod, connecting-rod, crank-rod, eccentric-rod, &c. It is attached to the pieces which it connects by two pins, about which it is free to turn. The effect of the link is to maintain the distance between the axes of those pins invariable; hence the common perpendicular of the axes of the pins is the line of connexion, and its extremities may be called the connected points. In a turning piece, the perpendicular let fall from its connected point upon its axis of rotation is the arm or crank-arm.
The axes of rotation of a pair of turning pieces connected by a link are almost always parallel, and perpendicular to the line of connexion in which case the angular velocity ratio at any instant is the reciprocal of the ratio of the common perpendiculars let fall from the line of connexion upon the respective axes of rotation.
If at any instant the direction of one of the crank-arms coincides with the line of connexion, the common perpendicular of the line of connexion and the axis of that crank-arm vanishes, and the directional relation of the motions becomes indeterminate. The position of the connected point of the crank-arm in question at such an instant is called a dead-point. The velocity of the other connected point at such an instant is null, unless it also reaches a dead-point at the same instant, so that the line of connexion is in the plane of the two axes of rotation, in which case the velocity ratio is indeterminate. Examples of dead-points, and of the means of preventing the inconvenience which they tend to occasion, will appear in the sequel.
§ 62. Coupling of Parallel Axes.—Two or more parallel shafts (such as those of a locomotive engine, with two or more pairs of driving wheels) are made to rotate with constantly equal angular velocities by having equal cranks, which are maintained parallel by a coupling-rod of such a length that the line of connexion is equal to the distance between the axes. The cranks pass their dead-points simultaneously. To obviate the unsteadiness of motion which this tends to cause, the shafts are provided with a second set of cranks at right angles to the first, connected by means of a similar coupling-rod, so that one set of cranks pass their dead points at the instant when the other set are farthest from theirs.
§ 63. Comparative Motion of Connected Points.—As the link is a rigid body, it is obvious that its action in communicating motion may be determined by finding the comparative motion of the connected points, and this is often the most convenient method of proceeding.
If a connected point belongs to a turning piece, the direction of its motion at a given instant is perpendicular to the plane containing the axis and crank-arm of the piece. If a connected point belongs to a shifting piece, the direction of its motion at any instant is given, and a plane can be drawn perpendicular to that direction.
The line of intersection of the planes perpendicular to the paths of the two connected points at a given instant is the instantaneous axis of the link at that instant; and the velocities of the connected points are directly as their distances from that axis.
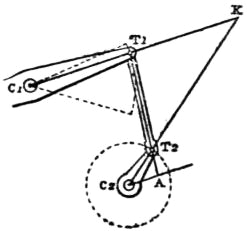 |
| Fig. 110. |
In drawing on a plane surface, the two planes perpendicular to the paths of the connected points are represented by two lines (being their sections by a plane normal to them), and the instantaneous axis by a point (fig. 110); and, should the length of the two lines render it impracticable to produce them until they actually intersect, the velocity ratio of the connected points may be found by the principle that it is equal to the ratio of the segments which a line parallel to the line of connexion cuts off from any two lines drawn from a given point, perpendicular respectively to the paths of the connected points.
To illustrate this by one example. Let C1 be the axis, and T1 the connected point of the beam of a steam-engine; T1T2 the connecting or crank-rod; T2 the other connected point, and the centre of the crank-pin; C2 the axis of the crank and its shaft. Let v1 denote the velocity of T1 at any given instant; v2 that of T2. To find the ratio of these velocities, produce C1T1, C2T2 till they intersect in K; K is the instantaneous axis of the connecting rod, and the velocity ratio is
Should K be inconveniently far off, draw any triangle with its sides respectively parallel to C1T1, C2T2 and T1T2; the ratio of the two sides first mentioned will be the velocity ratio required. For example, draw C2A parallel to C1T1, cutting T1T2 in A; then
§ 64. Eccentric.—An eccentric circular disk fixed on a shaft, and used to give a reciprocating motion to a rod, is in effect a crank-pin of sufficiently large diameter to surround the shaft, and so to avoid the weakening of the shaft which would arise from bending it so as to form an ordinary crank. The centre of the eccentric is its connected point; and its eccentricity, or the distance from that centre to the axis of the shaft, is its crank-arm.
An eccentric may be made capable of having its eccentricity altered by means of an adjusting screw, so as to vary the extent of the reciprocating motion which it communicates.
§ 65. Reciprocating Pieces—Stroke—Dead-Points.—The distance between the extremities of the path of the connected point in a reciprocating piece (such as the piston of a steam-engine) is called the stroke or length of stroke of that piece. When it is connected with a continuously turning piece (such as the crank of a steam-engine) the ends of the stroke of the reciprocating piece correspond to the


