new bars meeting there, is called a simple frame; it is obviously
just rigid. The stresses produced by extraneous forces in a
simple frame can be found by considering the equilibrium of the
various joints in a proper succession; and if the graphical method
be employed the various polygons of force can be combined into
a single force-diagram. This procedure was introduced by
W. J. M. Rankine and J. Clerk Maxwell (1864). It may be
noticed that if we take an arbitrary pole in the force-diagram,
and draw a corresponding funicular in the skeleton diagram
which represents the frame together with the lines of action
of the extraneous forces, we obtain two complete reciprocal
figures, in Maxwell’s sense. It is accordingly convenient to
use Bow’s notation (§ 5), and to distinguish the several compartments
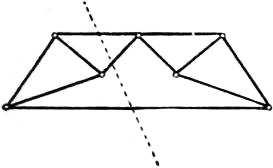
of the frame-diagram by letters. See fig. 33, where the
successive triangles in the diagram of forces may be constructed
in the order XYZ, ZXA, AZB. The class of “simple” frames
includes many of the frameworks used in the construction of
roofs, lattice girders and suspension bridges; a number of examples
will be found in the article Bridges. By examining the
senses in which the respective forces act at each joint we can ascertain
which members are in tension and which are in thrust; in
fig. 33 this is indicated by the directions of the arrowheads.
 |
| Fig. 33. |
 |
| Fig. 34. |
When a frame, though just rigid, is not “simple” in the above sense, the preceding method must be replaced, or supplemented, by one or other of various artifices. In some cases the method of sections is sufficient for the purpose. If an ideal section be drawn across the frame, the extraneous forces on either side must be in equilibrium with the forces in the bars cut across; and if the section can be drawn so as to cut only three bars, the forces in these can be found, since the problem reduces to that of resolving a given force into three components acting in three given lines (§ 4). The “critical case” where the directions of the three bars are concurrent is of course excluded. Another method, always available, will be explained under “Work” (§ 9).
When extraneous forces act on the bars themselves the stress in each bar no longer consists of a simple longitudinal tension or thrust. To find the reactions at the joints we may proceed as follows. Each extraneous force W acting on a bar may be replaced (in an infinite number of ways) by two components P, Q in lines through the centres of the pins at the extremities. In practice the forces W are usually vertical, and the components P, Q are then conveniently taken to be vertical also. We first alter the problem by transferring the forces P, Q to the pins. The stresses in the bars, in the problem as thus modified, may be supposed found by the preceding methods; it remains to infer from the results thus obtained the reactions in the original form of the problem. To find the pressure exerted by a bar AB on the pin A we compound with the force in AB given by the diagram a force equal to P. Conversely, to find the pressure of the pin A on the bar AB we must compound with the force given by the diagram a force equal and opposite to P. This question arises in practice in the theory of “three-jointed” structures; for the purpose in hand such a structure is sufficiently represented by two bars AB, BC. The right-hand figure represents a portion of the force-diagram; in particular ZX→ represents the pressure of AB on B in the modified problem where the loads W1 and W2 on the two bars are replaced by loads P1, Q1, and P2, Q2 respectively, acting on the pins. Compounding with this XV→, which represents Q1, we get the actual pressure ZV→ exerted by AB on B. The directions and magnitudes of the reactions at A and C are then easily ascertained. On account of its practical importance several other graphical solutions of this problem have been devised.
 |
| Fig. 35. |
§ 7. Three-dimensional Kinematics of a Rigid Body.—The position of a rigid body is determined when we know the positions of three points A, B, C of it which are not collinear, for the position of any other point P is then determined by the three distances PA, PB, PC. The nine co-ordinates (Cartesian or other) of A, B, C are subject to the three relations which express the invariability of the distances BC, CA, AB, and are therefore equivalent to six independent quantities. Hence a rigid body not constrained in any way is said to have six degrees of freedom. Conversely, any six geometrical relations restrict the body in general to one or other of a series of definite positions, none of which can be departed from without violating the conditions in question. For instance, the position of a theodolite is fixed by the fact that its rounded feet rest in contact with six given plane surfaces. Again, a rigid three-dimensional frame can be rigidly fixed relatively to the earth by means of six links.
 | |
| Fig. 36. | Fig. 37. |
The six independent quantities, or “co-ordinates,” which serve to specify the position of a rigid body in space may of course be chosen in an endless variety of ways. We may, for instance, employ the three Cartesian co-ordinates of a particular point O of the body, and three angular co-ordinates which express the orientation of the body with respect to O. Thus in fig. 36, if OA, OB, OC be three mutually perpendicular lines in the solid, we may denote by θ the angle which OC makes with a fixed direction OZ, by ψ the azimuth of the plane ZOC measured from some fixed plane through OZ, and by φ the inclination of the plane COA to the plane ZOC. In fig. 36 these various lines and planes are represented by their intersections with a unit sphere having O as centre. This very useful, although unsymmetrical, system of angular co-ordinates was introduced by L. Euler. It is exemplified in “Cardan’s suspension,” as used in connexion with a compass-bowl or a gyroscope. Thus in the gyroscope the “flywheel” (represented by the globe in fig. 37) can turn about a diameter OC of a ring which is itself free to turn about a diametral axis OX at right angles to the former; this axis is carried by a second ring which is free to turn about a fixed diameter OZ, which is at right angles to OX.
We proceed to sketch the theory of the finite displacements of a rigid body. It was shown by Euler (1776) that any displacement
