§ 5. In support of an affirmative answer to the former of these two questions, several different kinds of proof are, or might be, offered.
(I.) For one plan we may make a direct appeal to experience, by collecting sets of statistics and observing what is their law of distribution. As remarked above, this has been done in a great variety of cases, and in some instances to a very considerable extent, by Quetelet and others. His researches have made it abundantly convincing that many classes of things and processes, differing widely in their nature and origin, do nevertheless appear to conform with a considerable degree of accuracy to one and the same[1] law. At least this is made plain for the more
- ↑ Commonly called the exponential law; its equation being of the form The curve corresponding to it cuts the axis of at right angles (expressing the fact that near the mean there are a large number of values approximately equal; after a time it begins to slope away rapidly towards the axis of ; (expressing the fact that the results soon begin to grow less common as we recede from the mean); and the axis of is an asymptote in both directions (expressing the fact that no magnitude, however remote from the mean, is strictly impossible; that is, every deviation, however excessive, will have to be encountered at length within the range of a sufficiently long experience). The curve is obviously symmetrical, expressing the fact that equal deviations from the mean, in excess and in defect, tend to occur equally often in the long run.
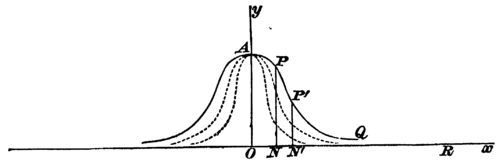
Illustration from Logic of Chance A rough graphic representation of the curve is given above. For the benefit of those unfamiliar with mathematics one or two brief remarks may be here appended concerning some of its properties. (1) It must




