lelogram of Fig. 4 the diagonal A C is the sum of A B and B C; or, since A D is geometrically equivalent to B C, A C is the geometrical sum of A B and A D.
| Fig. 3. | Fig. 4. |
All this is purely conventional. It simply amounts to this: that we choose to call paths having the relations I have described equal or added. But, though it is a convention, it is a convention with a good reason. The rule for geometrical addition may be applied not only to paths, but to any other things which can be represented by paths. Now, as a path is determined by the varying direction and distance of the point which moves over it from the starting-point, it follows that anything which from its beginning to its end is determined by a varying direction and a varying magnitude is capable of being represented by a line. Accordingly, velocities may be represented by lines, for they have only directions and rates. The same thing is true of accelerations, or changes of velocities. This is evident enough in the case of velocities; and it becomes evident for accelerations if we consider that precisely what velocities are to positions—namely, states of change of them—that accelerations are to velocities.
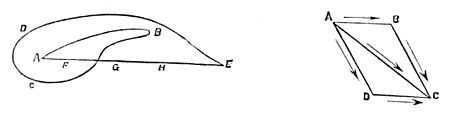
The so-called "parallelogram of forces" is simply a rule for compounding accelerations. The rule is, to represent the accelerations by paths, and then to geometrically add the paths. The geometers, however, not only use the "parallelogram of forces" to compound different accelerations, but also to resolve one acceleration into a sum of several. Let A B (Fig. 5) be the path which represents a certain  Fig. 5. acceleration—say, such a change in the motion of a body that at the end of one second the body will, under the influence of that change, be in a position different from what it would have had if its motion had continued unchanged such that a path equivalent to A B would lead from the latter position to the former. This acceleration may be considered as the sum of the accelerations represented by A C and C B. It may also be considered as the sum of the very different accelerations represented by A D and D B, where A B is almost the opposite of A C. And it is clear that there is an immense variety of
Fig. 5. acceleration—say, such a change in the motion of a body that at the end of one second the body will, under the influence of that change, be in a position different from what it would have had if its motion had continued unchanged such that a path equivalent to A B would lead from the latter position to the former. This acceleration may be considered as the sum of the accelerations represented by A C and C B. It may also be considered as the sum of the very different accelerations represented by A D and D B, where A B is almost the opposite of A C. And it is clear that there is an immense variety of
