tions in apparent size and distance of the binocular image are very striking, while the perspective in the picture remains clear but also variable. If the stereograph be that of a reversed cone, this becomes apparently shallow, small, and near, or deep, large, and remote, according
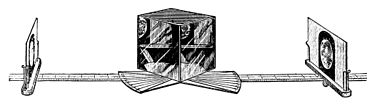
Fig. 12.—The Graduated Reflecting Stereoscope.
as the excess of strain is upon the internal or the external rectus muscles. This instrument, indeed, is useful in quite a variety of binocular experiments. The visual effects are the same as those from an adjustable stereoscope with semi-lenses, but the limits of variation are far wider, and it is a decided advantage to obtain direct measurement of the optic angle.
Such experiments show very conclusively that the current theory of visual triangulation, whatever may be its application to normal binocular vision, has to be entirely discarded as an explanation of stereoscopic vision. As a theory it is beautifully simple, and at first glance appears eminently satisfactory; the only objection to it in relation to the stereoscope consists in the fact that it is untrue. Its expression may be found in most of our text-books of physics, and the diagram usually employed in explaining the stereoscope is that of Fig. 13, which is taken from Helmholtz's "Physiological Optics," the only change being in the avoidance of Greek lettering. This slight change also is made in the following translation from the French edition of this work, which received the last corrections of the distinguished author, who is universally recognized as the highest living authority on the subject of which it treats. After describing the arrangement of the prism-like semi-lenses, he writes: "The two drawings are placed, side by side, upon the same sheet. The right eye, R, looks upon the drawing, a b, through the prism, p; the left eye, L, looks upon the drawing. a' b', through the prism, p'; the partition, g, prevents each eye from seeing the drawing intended for the other. The rays, c p and c' p', sent forth by the drawings, are refracted by the prisms, following the directions p R and p' L, the prolongations of which cut each other at C. The convexity of the surfaces of the prisms has the effect of diminishing at the same time the divergence of the sheafs of rays, so that each eye sees at A B an image of the drawing that is presented to it. The object appears in relief at A B."
This explanation is distinctly geometric, the locality of each point of the image perceived being determined by intersection of visual lines,
