Popular Science Monthly/Volume 4/April 1874/Images and Shadows
| IMAGES AND SHADOWS. |
By W. J. YOUMANS, M. D.
SO much has been said lately of the wonders of spectrum analysis, that we are very apt to forget the other and equally marvelous properties of the agent by which it is produced. Spectrum analysis is a rare and curious experiment, but the more familiar effects of light which we daily experience are really just as wonderful, if we will but pause to reflect upon them. Science means knowledge, and the science of optics embodies our knowledge of light; but how much, after all, do we know of it? A great deal, undoubtedly, of its modes of action, but very little, if any thing, of its nature. We have an hypothesis or supposition about it, and work out ingenious conclusions, logically and experimentally, and say that they are proved; but how far are we from comprehending them.
That light moves at an amazing velocity, is shown in several ways; and all the methods bring us to about the same results which are expressed in numbers and are demonstrably true; but what finite mind can enter into the meaning of the statement that the luminous ray moves forward at the rate of 185,000 miles in a second of time? Between the two ticks of a second's pendulum, we are told that light
Fig. 1.

Rectilinear Propagation of Light.
would pass round our globe seven and a half times. But who has a notion even of the dimensions of our globe? The number of thousands of miles through it and around it have been calculated, and the calculations harmonize with the whole body of astronomical knowledge; but we can form no adequate conception of such magnitudes. We patch together different shreds of our mental experience of large things, and construct a symbolic idea which represents our planet, but we never grasp the reality in the immensity of its proportions.
Light is a force, and science holds that it is made up of impulses. Nature has been shown to conform all kinds of dynâmical effects to rhythmical pulsing, or wave-like action and the impulses of light are held to be of the same kind. There are, at any rate, measurable effects which are unequal in the different colored lights, and the scale has been determined. In an inch of violet light it is shown that there are no less than 57,000 waves, a statement in which there is nothing extraordinary or impossible, as Nobert, the German optician, is in the habit of ruling his microscopical test-glasses at rates all the way from 100,000 to 200,000 per inch. But, when we are told that the ray enters the eye at the rate of 185,000 miles per second, and—as each inch contains 57,000 waves—that when we are looking at a violet object there are 699,000,000,000,000 beats upon the retina each second, the statement baffles all imagination: we may accept, but cannot understand it. In the attempt to penetrate the nature of light we are lost in the mysteries of the infinite. Yet the modes of its action have been determined, and they furnish the most splendid example we know of the inflexibleness and exactitude of what are called the laws of Nature.
Fig. 2.

Image formed by a Hole in a Card.
Man is placed in the midst of the universe, and is designed to have knowledge of it. He is impressible to outward agencies, and possesses a grand cerebral treasury-house for storing up these external impressions. Touch, taste, smell, and hearing, are the senses by which he becomes acquainted with many properties of things immediately around him; but the universe is reported to him through the sense of vision and by the agency of light. Somehow, in their mysterious nature, the luminous rays from all sources, distant and remote, effect a change in the nerve-structure of the eye by which impressions are transmitted to the brain. Into that mode of action we cannot now enter, but will confine our attention at present to the property of light by which luminous images are produced. For it is, after all, the images of things we have to deal with. We know the external world in its distances, forms, and colors, because its visible objects are all duplicated in the eye. The cloud, the landscape, the cathedral, that excites our thought and kindles our feeling, is, in each case, but a picture recreated from the external object by the agency of light.
Fig. 3.

Inverted Image of Landscape.
The first property, or law, of light, upon which the production of images depends, is simply that it moves in straight lines through any uniform medium that it can traverse. We are all familiar with the general fact that the path of light is rectilinear, but it may be accurately proved by a very simple experiment.
Two screens, A, B (Fig. 1), each pierced with a minute hole, are so arranged that the apertures are in a line with the flame of a candle, C. An eye, placed in this line behind the screens, is then able to see the flame; but, if the eye, the candle, or either screen, be slightly displaced to the right or left, the ray is interrupted, and the flame becomes invisible.
This propagation of light in straight lines, though the first condition of the production of images, is not the only condition; for, in that case, the images of illuminated objects would be repeated everywhere, and, when the blinds were opened, a picture of the landscape might be thrown, through the window, upon the opposite wall of a room. For the formation of an image, the rays of an object must be collected and passed through an aperture. This is shown by a simple experiment illustrated in Fig. 2. A card is pierced with a large pin-hole and held between a candle and screen, when an image of the candle will be formed upon the screen in an inverted position. That the image must be upside-down is evident, if the rays take a straight course. A line from the top of the candle-flame through the puncture is prolonged to the bottom of the image, and another, from the bottom of the flame, crosses the first at the aperture, and strikes the top of the
Fig. 4.

Image of Sun upon the Floor.
image. A line from the centre of the candle passes straight through and strikes the centre of the image, while lines from the two sides of the flame cross again, and are prolonged to the opposite sides of the image. Thus, as each point upon the screen receives only the light from a corresponding point of the flame, the image repeats the object in outline, color, and brightness, though in a reversed position.
This principle may be applied on a larger scale. Let a room be made quite dark, and a white screen be placed opposite a small hole in the shutter. There will then be formed upon the white surface an inverted picture of the external objects, as shown in Fig. 3. They will appear of the natural colors, and the outlines will be sharper in proportion as the hole is smaller.
When the sun shines through a small orifice into a darkened room, a cone of rays is produced, as everybody has observed, by lighting up the particles of dust which are scattered in its course; for, if the air were quite clear, the track of the rays would be invisible. In this case an image of the sun is formed upon the floor or opposite wall by
Fig. 5.

Images of Sun formed by Foliage.
the crossing of the rays through the aperture, exactly in the manner of the production of the candle-image and the landscape-picture just described. The best condition for the formation of such an image is when the sun is low, and there is a white wall opposite to receive it; the image is then perfectly circular. But if the light falls upon the floor, as represented in Fig. 4, the cone of rays produces an oblong or elliptical image; the deviation from an exact circle depends upon the angle which the cone of rays makes with the floor. Such an image may often be made instructive in observing solar phenomena. By closely examining it, it is sometimes possible to detect the presence of spots on the solar surface. Solar eclipses may be watched in the same way. As the moon gradually encroaches upon the sun's disk its progress can be traced by a corresponding change in the form of the image, which resembles that of the uneclipsed portion of the solar surface. In such observations, however, it will be remembered that the course of the movement is always reversed. It was in this way that the transit of Venus was first observed by Jeremiah Horrocks, November 24, 1639. He had calculated the time, which fell upon Sunday morning. He arranged his room for the observation, and then went to church, as he did not wish any secular interests to interfere with religious devotion. It is very probable, however, that Venus was mixed up with his devout meditations, for he hurried back from service, and was delighted to find that his calculations were verified, as the planet was already far advanced in its passage across the sun's face.
We are all familiar with similar images of the sun, of a round or oval outline, formed upon the ground where his rays shine through small openings in the foliage of trees, as illustrated in Fig. 5.
Fig. 6.

Formation of a Shadow.
The same property, that is, the rectilinear propagation of light, gives rise to a reverse effect, or a sort of dark image or shadow, although a shadow depending upon the absence of light is of course not properly an image. "Let the source of light be a luminous point, and let an opaque body be placed so as to intercept a portion of its rays (Fig. 6). If we construct a conical surface touching the body all round, and having its vertex at the luminous point, it is evident that all the space within this surface on the farther side of the opaque body is completely screened from the rays. The cone thus constructed is called the shadow-cone, and its intersection with any surface behind the opaque body defines the shadow cast upon that surface. In the case which we have been supposing—that of a luminous point—the shadow-cone and the shadow itself will be sharply defined."
Actual sources of light are not, however, mere points; they have finite and variable dimensions, and this complicates the effect in the geometry of shadows. These effects are well illustrated by the diagram (Fig. 7). Let the central sphere represent a source of light placed between two opaque spheres, one larger and the other smaller than itself. We shall then have two kinds of shadow, the total shadow or umbra, and the partial shadow or penumbra. If the opaque sphere, seen at the right in the diagram, be smaller than the luminous body, the umbra terminates at a finite distance depending upon the relative magnitudes and the proximity of the two bodies. If the opaque body is larger than the source of illumination, as illustrated in the left portion of the diagram, the cone of the umbra is projected to an infinite distance. The penumbral cones represented
Fig. 7.
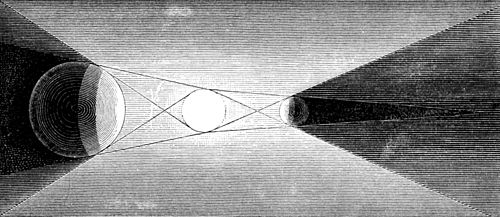
Umbra and Penumbra.
by a lighter shading, it is seen, are wider than the cones of total shadow, and include them. It will be noticed that all points lying within the penumbral cones are excluded from the view of some portion of the luminous body, and are thus partially shaded by the opaque bodies. Points that are very near the outer boundaries are very slightly darkened, if near the total shadow they are almost completely shaded. The penumbra is, therefore, not a uniform shadow, but gradually fades into darkness from its outer limit to the total obscuration of the umbra. It follows from this that the shadow of an opaque body falling upon a screen will not have a sharply-defined edge, but will show a transition from total shadow to the complete absence of shadow. To have the shadow clean and sharp at its edge, it would be necessary to have the source of illumination a mere point. Of course the effect of such abrupt transitions from perfect illumination to total darkness, if it were the plan of Nature, would be most inconvenient and painful, if not destructive to the eyes. We are protected from this by the phenomena of double shadows, and the gradual passage from darkness to light, although each luminous ray moves undeviatingly in its straight line. Light cannot turn corners like sound. This is explained by the excessive shortness of the luminous as compared with sonorous waves. Sound-waves are so large that they flow around objects in the air, and consequently cast but feeble shadows, although Deschanel (from whose admirable work on "Natural Philosophy" our cuts are borrowed) states that Collodon, in his experiments on the transmission of sound through the water of the Lake of Geneva, established the presence of a very sharply-defined sound-shadow in the water behind the end of a projecting wall.
It is necessary to say, however, that the foregoing statement that light cannot turn corners is only true in the common and general experience of it. If we carry our experiments with light down to so fine a point that we reach the dimensions of its waves, it is then found that they are capable of bending round obstacles. If sunlight be allowed to pass through an exceedingly fine slit, and then to fall on a screen of white paper, colored bands appear, called diffraction fringes; that is, the white light, in its passage through the minute opening, has been interfered with and broken up into its component colors. We have here, however, a new order of effects which will require to be separately considered.