The Elements of Euclid for the Use of Schools and Colleges/Book XI
BOOK XI.
DEFINITIONS.
1. A solid is that which has length, breadth, and thickness.
2. That which bounds a solid is a superficies.
3. A straight line is perpendicular, or at right angles, to a plane, when it makes right angles with every straight line meeting it in that plane.
4. A plane is perpendicular to a plane, when the straight lines drawn in one of the planes perpendicular to the common section of the two planes, are perpendicular to the other plane.
5. The inclination of a straight line to a plane is the acute angle contained by that straight line, and another drawn from the point at which the first line meets the plane to the point at which a perpendicular to the plane drawn from any point of the first line above the plane, meets the same plane.
6. The inclination of a plane to a plane is the acute angle contained by two straight lines drawn from any the same point of their common section at right angles to it, one in one plane, and the other in the other plane.
7. Two planes are said to have the same or a like inclination to one another, which two other planes have, when the said angles of inclination are equal to one another.
8. Parallel planes are such as do not meet one another though produced. 9. A solid angle is that which is made by more than two plane angles, which are not in the same plane, meeting at one point.
10. Equal and similar solid figures are such as are contained by similar planes equal in number and magnitude. [See the Notes.]
11. Similar solid figures are such as have all their solid angles equal, each to each, and are contained by the same number of similar planes.
12. A pyramid is a solid figure contained by planes which are constructed between one plane and one point above it at which they meet.
13. A prism is a solid figure contained by plane figures, of which two that are opposite are equal, similar, and parallel to one another; and the others are parallelograms.
14. A sphere is a solid figure described by the revolution of a semicircle about its diameter, which remains fixed.
15. The axis of a sphere is the fixed straight line about which the semicircle revolves.
16. The centre of a sphere is the same with that of the semicircle.
17. The diameter of a sphere is any straight line which passes through the centre, and is terminated both ways by the superficies of the sphere.
18. A cone is a solid figure described by the revolution of a right-angled triangle about one of the sides containing the right angle, which side remains fixed.
If the fixed side be equal to the other side containing the right angle, the cone is called a right-angled cone; if it be less than the other side, an obtuse-angled cone; and if greater, an acute-angled cone.
19. The axis of a cone is the fixed straight line about which the triangle revolves. 20. The base of a cone is the circle described by that side containing the right angle which revolves.
21. A cylinder is a solid figure described by the revolution of a right-angled parallelogram about one of its sides which remains fixed.
22. The axis of a cylinder is the fixed straight line about which the parallelogram revolves.
23. The bases of a cylinder are the circles described by the two revolving opposite sides of the parallelogram.
24. Similar cones and cylinders are those which have their axes and the diameters of their bases proportionals.
25. A cube is a solid figure contained by six equal squares.
26. A tetrahedron is a solid figure contained by four equal and equilateral triangles.
27. An octahedron is a solid figure contained by eight equal and equilateral triangles.
28. A dodecahedron is a solid figure contained by twelve equal pentagons which are equilateral and equiangular.
29. An icosahedron is a solid figure contained by twenty equal and equilateral triangles.
A. A parallelepiped is a solid figure contained by six quadrilateral figures, of which every opposite two arc parallel.
PROPOSITION 1. THEOREM.
One part of a straight line cannot he in a plane, and another other part without it.
If it be possible, let AB, part of the straight line ABC, be in a plane, and the part BC without it.
 Then since the straight line AB is in the plane, it can be produced in that plane; let it be produced to D; and let any plane pass through the straight line,and be turned about until it pass through the point C.
Then since the straight line AB is in the plane, it can be produced in that plane; let it be produced to D; and let any plane pass through the straight line,and be turned about until it pass through the point C.
Then, because the points B and C are in this plane, the straight line BC is in it. [I. Definition 7.
Therefore there are two straight lines ABC, ABD in the same plane, that have a common segment AB;
but this is impossible. [I. 11, Corollary.
Wherefore, one part of a straight line &c. q.e.d.
PROPOSITION 2. THEOREM.
Two straight lines which cut one another are in one plane; and three straight lines which meet one another are in one plane.
Let the two straight lines AB, CD cut one another at E: AB and CD shall be in one plane; and the three straight lines EC, CB, BE which meet one another, shall be in one plane.
 Let any plane pass through the straight line EB, and let the plane be turned about EB, produced if necessary, until it pass through the point C.
Let any plane pass through the straight line EB, and let the plane be turned about EB, produced if necessary, until it pass through the point C.
Then, because the points E and C are in this plane, the straight line EC is in it; [I. Definition 7.
for the same reason, the straight line BC is in the same plane;
and, by hypothesis, EB is in it.
Therefore the three straight lines EC, CB, BE are in one plane.
But AB and CD are in the plane in which EB and EC are; [XI. 1.
therefore AB and CD are in one plane.
PROPOSITION 3. THEOREM.
If two planes cut one another their common section is a straight line.
Let two planes AB, BC cut one another, and let BD be their common section: BD shall be a straight line.
 If it be not, from B to D, draw in the plane AB the straight line BED, and in the plane BC the straight line BFD. [Postulate 1.
If it be not, from B to D, draw in the plane AB the straight line BED, and in the plane BC the straight line BFD. [Postulate 1.
Then the two straight lines BED, BFD have the same extremities, and therefore include a space between them;
but this is impossible. [Axiom 10.
Therefore BD, the common section of the planes AB and BC cannot but be a straight line.
Wherefore, if two planes &c. q.e.d.
PROPOSITION 4. THEOREM.
If a straight line stand at right angles to each of two straight lines at the point of their intersection, it shall also he at right angles to the plane which passes through them, that is, to the plane in which they are.
 Let the straight line EF stand at right angles to each of the straight lines AB, CD, at E, the point of their intersection: EF shall also be at right angles to the plane passing through AB, CD.
Let the straight line EF stand at right angles to each of the straight lines AB, CD, at E, the point of their intersection: EF shall also be at right angles to the plane passing through AB, CD.
Take the straight lines AE, EB, CE, ED, all equal to one another; join AD, CB; through E draw in the plane in which are AB, CD, any straight line cutting AD at G, and CB at H: and from any point F in EF draw FA, FG, FD, FC, FH, FB. Then, because the two sides AE, ED are equal to the two sides BE,EC, each to each, [Construction.
and that they contain equal angles AED, BEC; [I. 15.
therefore the base AD is equal to the base BC, and the angle DAE is equal to the angle EBC. [I. 4.
And the angle AEG is equal to the angle BEH; [I. 15.
therefore the triangles AEG, BEH have two angles of the one equal to two angles of the other, each to each;
and the sides EA, EB adjacent to the equal angles are equal to one another; [Construction.
therefore EG is equal to EH, and AG is equal to BH. [I. 26.
And because EA is equal to EB, [Construction.
and EF is common and at right angles to them, [Hypothesis.
therefore the base AF is equal to the base BF. [I. 4.
For the same reason CF is equal to DF.
And since it has been shewn that the two sides DA, AF are equal to the two sides CB, BF, each to each,
and that the base DF is equal to the base CF;
therefore the angle DAF is equal to the angle CBF. [I. 8.
Again, since it has been shewn that the two sides FA, AG are equal to the two sides FB, BH, each to each,
and that the angle FAG is equal to the angle FBH;
therefore the base FG is equal to the base FH. [I. 4.
Lastly, since it has been shewn that GE is equal to HE, and EF is common to the two triangles FEG, FEH;
and the base FG has been shewn equal to the base FH;
therefore the angle FEG is equal to the angle FEH. [I. 8.
Therefore each of these angles is a right angle. [I, Defn. 10.
In like manner it may be shewn that EF makes right angles with every straight line which meets it in the plane passing through AB, CD.
Therefore EF is at right angles to the plane in which are AB, CD. [XI. Definition 3.
PROPOSITION 5. THEOREM.
If three straight lines meet all at one point, and a straight line stand at right angles to each of them at that point, the three straight lines shall he in one and the same plane.
Let the straight line AB stand at right angles to each of the straight lines BC, BD, BE, at B the point where they meet: BC, BD, BE shall be in one and the same plane.
 For, if not, let, if possible, BD and BE be in one plane, and BC without it; let a plane pass through AB and BC; the common section of this plane with the plane in which are BD and BE is a straight line; [XI. 3.
For, if not, let, if possible, BD and BE be in one plane, and BC without it; let a plane pass through AB and BC; the common section of this plane with the plane in which are BD and BE is a straight line; [XI. 3.
let this straight line be BF.
Then the three straight lines AB, BC, BF are all in one plane, namely, the plane which passes through AB and BC.
And because AB stands at right angles to each of the straight lines BD, BE, [Hypothesis.
therefore it is at right angles to the plane passing through them; [XI. 4.
therefore it makes right angles with every straight line meeting it in that plane. [XI. Definition 3.
But BF meets it, and is in that plane;
therefore the angle ABF is a right angle.
But the angle ABC is, by hypothesis, a right angle;
therefore the angle ABC is equal to the angle ABF; [Ax. 11.
and they are in one plane; which is impossible. [Axiom 9.
Therefore the straight line BC is not without the plane in which are BD and BE,
therefore the three straight lines BC, BD, BE are in one and the same plane.
PROPOSITION 6. THEOREM.
If two straight lines be at right angles to the same plane, they shall be parallel to one another.
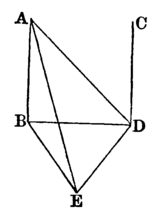 Let the straight lines AB, CD be at right angles to the same plane: AB shall be parallel to CD.
Let the straight lines AB, CD be at right angles to the same plane: AB shall be parallel to CD.
Let them meet the plane at the points B,D; join BD; and in the plane draw DE at right angles to BD; [1. 11.
make DE equal to AB; [I. 3.
and join BE,AE,AD.
Then, because AB is perpendicular to the plane, [Hypothesis.
it makes right angles with every straight line meeting it in that plane. [XI. Def. 3.
But BD and BE meet AB, and are in that plane,
therefore each of the angles ABD, ABE is a right angle. For the same reason each of the angles CDB, CDE is a right angle.
And because AB equal to ED, [Construction.
and BD is common to the two triangles ABD, EDB,
the two sides AB, BD are equal to the two sides ED, DB, each to each;
and the angle ABD is equal to the angle EDB, each of them being a right angle; [Axiom 11.
therefore the base AD is equal to the base EB. [I. 4.
Again, because AB is equal to ED, [Construction.
and it has been shewn that BE is equal to DA;
therefore the two sides AB, BE are equal to the two sides ED, DA, each to each;
and the base AE is common to the two triangles ABE, EDA;
therefore the angle ABE is equal to the angle EDA. [I 8.
But the angle ABE is a right angle,
therefore the angle EDA is a right angle,
that is, ED is at right angles to AD.
 But ED is also at right angles to each of the two BD, CD;
But ED is also at right angles to each of the two BD, CD;
therefore ED is at right angles to each of the three straight lines BD, AD, CD, at the point at which they meet;
therefore these three straight lines are all in the same plane. [XI. 5.
But AB is in the plane in which are BD, DA; [XI. 2.
therefore AB, BD, CD are in one plane.
And each of the angles ABD, CDB is a right angle;
therefore AB is parallel to CD. [I. 28.
Wherefore, if two straight lines &c. q.e.d.
PROPOSITION 7. THEOREM.
If two straight lines he parallel, the straight line drawn from any point in one to any point in the other, is in the same plane with the parallels.
Let AB, CD be parallel straight lines, and take any point E in one and any point F in the other: the straight line which joins E and F shall be in the same plane with the parallels.
 For, if not, let it be, if possible, without the plane, as EGF; and in the plane ABCD, in which the parallels are, draw the straight EGF,EHF from E to F.
For, if not, let it be, if possible, without the plane, as EGF; and in the plane ABCD, in which the parallels are, draw the straight EGF,EHF from E to F.
Then, since EGF is also a straight line, [Hypothesis.
the two straight lines EGF, EHF include a space between them; which is impossible. [Axiom 10.
Therefore the straight line joining the points E and F is not without the plane in which the parallels AB, CD are;
therefore it is in that plane.
PROPOSITION 8. THEOREM.
If two straight lines he parallel, and one of them be at right angles to a plane, the other also shall he at right angles to the same plane.
Let AB, CD be two parallel straight lines; and let one of them AB be at right angles to a plane: the other CD shall be at right angles to the same plane.
 Let AB, CD meet the plane at the points B, D; join BD; therefore AB, CD, BD are in one plane. [XI. 7.
Let AB, CD meet the plane at the points B, D; join BD; therefore AB, CD, BD are in one plane. [XI. 7.
In the plane to which AB is at right angles, draw DE at right angles to BD; [I. 11.
make DE equal to AB; [I 3.
and join BE,AE,AD.
Then, because AB is at right angles to the plane, [Hypothesis.
it makes right angles with every straight line meeting it in that plane; [XI. Definition 3.
therefore each of the angles ABD, ABE is a right angle.
And because the straight line BD meets the parallel straight lines AB, CD,
the angles ABD, CDB are together equal to two right angles, [I. 29.
But the angle ABD is a right angle, [Hypothesis. therefore the angle CDB is a right angle;
that is, CD is at right angles to BD.
And because is equal to ED, [Construction.
and BD is common to the two triangles ABD, EDB;
the two sides AB, BD are equal to the two sides ED, DB, each to each;
and the angle ABD is equal to the angle EDB, each of them being a right angle; [Axiom 11.
therefore the base AD is equal to the base EB. [I. 4.
Again, because AB is equal to ED, [Construction.
and BE has been shewn equal to DA,
the two sides AB, BE are equal to the two sides ED DA, each to each;
 and the base AE is common to the two triangles ABE, EDA;
and the base AE is common to the two triangles ABE, EDA;
therefore the angle ABE is equal to the angle ADE. [I. 8.
But the angle ABE is a right angle;
therefore the angle ADE is a right angle;
that is, ED is at right angles to AD.
But ED is at right angles to BD, [Const.
therefore ED is at right angles to the plane which passes through BD, DA, [XI. 4.
and therefore makes right angles with every straight line meeting it in that plane. [XI. Definition 3.
But CD is in the plane passing through BD, DA, because all three are in the plane in which are the parallels AB, CD;
therefore ED is at right angles to CD,
and therefore CD is at right angles to ED.
But CD was shewn to be at right angles to BD;
therefore CD is at right angles to the two straight lines BD, ED, at the point of their intersection D,
and is therefore at right angles to the plane passing through BD, ED, [XI. 4,
that is, to the plane to which AB is at right angles.
Wherefore, if two straight lines &c. q.e.d.
PROPOSITION 9. THEOREM.
Two straight lines which are each of them parallel to the same straight line, and not in the same plane with it, are parallel to one another.
 Let AB and CD be each of them parallel to EF, and not in the same plane with it: AB shall be parallel to CD.
Let AB and CD be each of them parallel to EF, and not in the same plane with it: AB shall be parallel to CD.
In EF take any point G; in the plane passing through EF and AB, draw from G the straight line GH at right angles to EF;
and in the plane passing through EF and CD, draw from G the straight line GK at right angles to EF. [I. 11.
Then, because EF is at right angles to GH and GK, [Construction.
EF is at right angles to the plane HGK passing through them. [XI. 4.
And EF is parallel to AB; [Hypothesis.
therefore AB is at right angles to the plane HGK. [XI. 8.
For the same reason CD is at right angles to the plane HGK.
Therefore AB and CD are both at right angles to the plane HGK.
Therefore AB is parallel to CD. [XI. 6.
Wherefore, if two straight lines &c. q.e.d.
PROPOSITION 10. THEOREM.
If two straight lines meeting one another he parallel to two others that meet one another, and are not in the same plane with the first two, the first two and the other two shall contain equal angles.
Let the two straight lines AB, BC, which meet one another, be parallel to the two straight lines DE, EF, which meet one another, and are not in the same plane with AB, BC: the angle ABC shall be equal to the angle DEF.
 Take BA, BC, ED, EF equal to one another, and join AD, BE, CF, AC, DF.
Take BA, BC, ED, EF equal to one another, and join AD, BE, CF, AC, DF.
Then, because AB is equal and parallel to DE,
therefore AD is equal and parallel to BE. [1. 33.
For the same reason, CF is equal and parallel to BE.
Therefore AD and CF are each of them equal and parallel to BE.
Therefore AD is parallel to CF, [XI. 9
and AD is also equal to CF, [Axiom 1.

Therefore AC is equal and parallel to DF. [I. 33.
And because AB, BC are equal to DE, EF, each to each,
and the base AC is equal to the base DF,
therefore the angle ABC is equal to the angle DEF. [I. 8.
Wherefore, if two straight lines &c. q.e.d.
PROPOSITION 11. PROBLEM.
To draw a straight line perpendicular to a given plane from a given point without it.
Let A be the given point without the plane BH: it is required to draw from the point A a straight line perpen- dicular to the plane BH.
 Draw any straight line BC in the plane BH, and from the point A draw AD perpendicular to BC. [1. 12.
Draw any straight line BC in the plane BH, and from the point A draw AD perpendicular to BC. [1. 12.
Then if AD be also perpendicular to the plane BH, the thing required is done.
But, if not, from the point D draw, in the plane BH, the straight line DE at right angles to BC, [I. 11.
and from the point A draw AF perpendicular to DE. [1. 12.
AF shall be perpendicular to the plane BH.
Through F draw GH parallel to BC. [I. 31. Then, because BC is at right angles to ED and DA, [Constr.
BC is at right angles to the plane passing through ED and DA. [XI. 4.
And GH is parallel to BC; [Construction.
therefore GH is at right angles to the plane passing through ED and DA; [XI. 8.
therefore GH makes right angles with every straight line meeting it in that plane. [XI. Definition 3.
But AF meets it, and is in the plane passing through ED and DA;
therefore GH is at right angles to AF,
and therefore AF is at right angles to GH.
But is also at right angles to DE; [Construction.
therefore AF is at right angles to each of the straight lines GH and DE at the point of their intersection;
therefore AF is perpendicular to the plane passing through GH and DE, that is, to the plane BH. [XI. 4.
Wherefore, from the given point A, without the plane BH, the straight line AF has been drawn perpendicular to the plane. q.e.f.
PROPOSITION 12. PROBLEM.
To erect a straight line at right angles to a given plane, from a given point in the plane.
Let A be the given point in the given plane: it is required to erect a straight line from the point A, at right angles to the plane.
 From any point B without the plane, draw BC perpendicular to the plane; [XI. 11.
From any point B without the plane, draw BC perpendicular to the plane; [XI. 11.
and from the point A draw AD parallel to BC, [I. 31.
AD shall be the straight line required.
For, because AD and BC are two parallel straight lines, [Constr.
and that one of them BC is at right angles to the given plane, [Construction.
the other AD is also at right angles to the given plane. [XI. 8,
PROPOSITION 13. THEOREM.
From the same point in a given plane, there cannot be two straight lines at right angles to the plane, on the same side of it; and there can he hut one perpendicular to a plane from, a point without the plane.
For, if it be possible, let the two straight lines AB,AC be at right angles to a given plane, from the same point A in the plane, and on the same side of it.
 Let a plane pass through BA, AC;
Let a plane pass through BA, AC;
the common section of this with the given plane is a straight line; [XI. 3.
let this straight line be DAE.
Then the three straight lines AB, AC, DAE are all in one plane.
And because CA is at right angles to the plane, [Hypothesis.
it makes right angles with every straight line meeting it in the plane. [XI. Definition 3.
But DAE meets CA, and is in that plane; therefore the angle CAE is a right angle. For the same reason the angle BAE is a right angle. Therefore the angle CAE is equal to the angle BAE; [Ax.ll.
and they are in one plane; which is impossible. [Axiom 9.
Also, from a point without the plane, there can be but one perpendicular to the plane.
For if there could be two, they would be parallel to one another, [XI. 6.
which is absurd.
PROPOSITION 14. THEOREM.
Planes to which the same straight line is perpendicular are parallel to one another.
Let the straight line AB he perpendicular to each of the planes CD and EF: these planes shall be parallel to one another.
 For, if not, they will meet one Smother when produced; let them meet, then their common section will be a straight line;
For, if not, they will meet one Smother when produced; let them meet, then their common section will be a straight line;
let GH be this straight line; in it take any point K, and join AK, BK.
Then, because AB is perpendicular to the plane EF, [Hyp.
it is perpendicular to the straight line BK which is in that plane; [XI. Definition 8.
therefore the angle ABK is a right angle.
For the same reason the angle BAK is a right angle.
Therefore the two angles ABK, BAK of the triangle ABK are equal to two right angles;
which is impossible. [I. 17
Therefore the planes CD and EF, though produced do not meet one another;
that is, they are parallel. [XI. Definition 8.
Wherefore, planes &c. q.e.d.
PROPOSITION 15. THEOREM.
If two straight lines which meet one another, be parallel to two other straight lines which meet one another, but are not in the same plane with the first two, the plane pass-ing through these is parallel to the plane passing through the others. Let AB,BC, two straight lines which meet one another, be parallel to two other straight lines DE, EF, which meet one another, but are not in the same plane with AB,BC: the plane passing through AB, BC, shall be parallel to the plane passing through DE, EF.
 From the point B draw BG perpendicular to the plane passing through DE, EF, [XI. 11.
From the point B draw BG perpendicular to the plane passing through DE, EF, [XI. 11.
and let it meet that plane at G;
through G draw GH parallel to ED, and G parallel to EF. [1.31.
Then, because BG is perpendicular to the plane passing through DE, EF, [Construction.
it makes right angles with every straight line meeting it in that plane; [XI. Definition 3.
but the straight lines GH and GK meet it, and are in that plane;
therefore each of the angles BGH and BGK is a right angle.
Now because BA is parallel to ED, [Hypothesis.
and GH is parallel to ED, [Construction.
therefore BA is parallel to GH; [XI. 9.
therefore the angles ABG and BGH are together equal to two right angles. [I. 29.
And the angle BGH has been shewn to be a right angle;
therefore the angle ABG is a right angle.
For the same reason the angle CBG is a right angle.
Then, because the straight line GB stands at right angles to the two straight lines BA, BC, at their point of intersection B,
therefore GB is perpendicular to the plane passing through BA,BC. [XI. 4.
And GB is also perpendicular to the plane passing through DE, EF. [Construction.
But planes to which the same straight line is perpendicular are parallel to one another; [XI. 14.
therefore the plane passing through AB, BC is parallel to the plane passing through DE, EF.
Wherefore, if two straight lines &c. q e.f.
PROPOSITION 16. THEOREM.
If two parallel planes be cut by another plane, their common sections with it are parallel.
Let the parallel planes AB, CD be cut by the plane EFHG, and let their common sections with it be EF, GH: EF shall be parallel to GH.
For if not, EF and GH, being produced, will meet either towards F, H, or towards E, G. Let them be produced and meet towards F, H at the point K.
 Then, since EFK is in the plane AB, every point in EFK is in that plane; [XI. 1.
Then, since EFK is in the plane AB, every point in EFK is in that plane; [XI. 1.
therefore K is in the plane AB.
For the same reason K is in the plane CD.
Therefore the planes AB, CD, being produced, meet one another.
But they do not meet, since they are parallel by hypothesis.
Therefore EF and GH, being produced, do not meet towards F, H.
In the same manner it may be shewn that they do not meet towards E, G.
But straight lines which are in the same plane, and which being produced ever so far both ways do not meet are parallel;
therefore EF is parallel to GH.
PROPOSITION 17. THEOREM.
If two straight lines be cut by parallel planes, they shall be cut in the same ratio.
Let the straight lines AB and CD be cut by the parallel planes GH, KL, MN, at the points A, E, B, and C,F,D: AE shall be to EB as CF is to FD.
 Join AC,BD,AD; let AD meet the plane KL at the point X; and join EX, XF.
Join AC,BD,AD; let AD meet the plane KL at the point X; and join EX, XF.
Then, because the two parallel planes KL, MN are cut by the plane EBDX, the common sections EX, BD are parallel; [XI. 16.
and because the two parallel planes GH, KL are cut by the plane AXFC, the common sections AC, XF are parallel. [XI. 16.
And, because EX is parallel to BD, a side of the triangle ABD,
therefore AE is to EB as AX is to XD. [VI. 2.
Again, because XF is parallel to AC, a side of the triangle ADC,
therefore AX is to XD as CF is to FD. [VI. 2.
And it was shewn that AX is to XD as AE is to EB;
therefore AE is to EB as CF is to FD. [V. 11.
Wherefore, if two straight lines &c. q.e.d.
PROPOSITION 18. THEOREM.
If a straight line be at right angles to a plane, every plane which passes through it shall be at right angles to that plane.
Let the straight line AB be at right angles to the plane CK: every plane which passes through AB shall be at right angles to the plane CK.
 Let any plane DE pass through AB and let CE be the common section of the planes DE, CK; [XI 3.
Let any plane DE pass through AB and let CE be the common section of the planes DE, CK; [XI 3.
take any point F in CE, from which draw FG, in the plane DE, at right angles to CE. [I. 11.
Then, because AB is, at right angles to the plane CK, [Hypothesis. therefore it makes right angles with every straight line meeting it in that plane; [XI. Definition 3. but CB meets it, and is in that plane; therefore the angle ABF is a right angle. But the angle GFB is also a right angle; [Construction, therefore FG is parallel to AB. [I. 28. And AB is at right angles to the plane CK; [Hypothesis. therefore FG is also at right angles to the same plane. [XI. 8.
But one plane is at right angles to another plane, when the straight lines drawn in one of the planes at right angles to their common section, are also at right angles to the other plane; [XI. Definition 4.
and it has been shewn that any straight line FG drawn in the plane DE, at right angles to CE, the common section of the planes, is at right angles to the other plane CK;
therefore the plane DE is at right angles to the plane CK.
In the same manner it may be shewn that any other plane which passes through AB is at right angles to the plane CK
Wherefore, if a straight line &c., q.e.d.
PROPOSITION 19. THEOREM.
If two planes which cut one another be each of them perpendicular to a third plane, their common section shall be perpendicular to the same plane. Let the two planes BA, BC be each of them perpendicular to a third plane, and let BD be the common section of the planes BA, BC: BD shall be perpendicular to the third plane.
 For, if not, from the point D, draw in the plane BA, the straight line DE at right angles to AD, the common section of the plane BA with the third plane; [I. 11.
For, if not, from the point D, draw in the plane BA, the straight line DE at right angles to AD, the common section of the plane BA with the third plane; [I. 11.
and from the point D, draw in the plane BC, the straight line DF at right angles to CD, the common section of the plane BC with the third plane. [I. 11.
Then, because the plane BA is perpendicular to the third plane, [Hypothesis.
and DE is drawn in the plane BA at right angles to AD their common section; [Construction.
therefore DE is perpendicular to the third plane. [XI. Def. 4.
In the same manner it may be shewn that DE is perpendicular to the third plane.
Therefore from the point D two straight lines are at right angles to the third plane, on the same side of it; which is impossible. [XI. 13.
Therefore from the point D, there cannot be any straight line at right angles to the third plane, except BD the common section of the planes BA, BC;
therefore BD is perpendicular to the third plane.
Wherefore, if two planes &c. q.e.d.
PROPOSITION 20. THEOREM.
If a solid angle be contained by three plane angles, any two of them are together greater than the third.
Let the solid angle at A be contained by the three plane angles BAC, CAD, DAB: any two of them shall be together greater than the third.
If the angles BAC, CAD, DAB be all equal, it is evident that any two of them are greater than the third.
 If they are not all equal, let BAC be that angle which is not less than either of the other two, and is greater than one of them, BAD.
If they are not all equal, let BAC be that angle which is not less than either of the other two, and is greater than one of them, BAD.
At the point A in the straight line BA, make, in the plane which passes
through BA, AC, the angle BAE equal to the angle BAD; [I.23. make AE equal to AD; [I. 3.
through E draw BEC cutting AB,AC at the points B,C; and join DB,DC.
Then, because AD is equal to AE, [Construction. and AB is. common to the two triangles BAD, BAE, the two sides BA, AD are equal to the two sides BA, AE, each to each;
and the angle BAD is equal to the angle BAE; [Constr.
therefore the base BD is equal to the base BE. [I. 4.
And because BD, DC are together greater than BC, [1. 20.
and one of them BD has been shewn equal to BE a part of EC.
therefore the other DC is greater than the remaining part EC.
And because AD is equal to AE, [Construction. and AC is common to the two triangles DAC, EAC, but the base DC is greater than the base EC;
therefore the angle DAC is greater than the angle EAC. [I. 25.
And, by construction, the angle BAD is equal to the angle BAE;
therefore the angles BAD, DAC are together greater than the angles BAE, EAC, that is, than the angle BAC.
But the angle BAC is not less than either of the angles BAD, DAC;
therefore the angle BAC together with either of the other angles is greater than the third.
Wherefore, if a solid angle &c. q.e.d. PROPOSITION 21. THEOREM.
Every solid angle is contained by plane angles, which are together less than four right angles.
First let the solid angle at A be contained by three plane angles BAC, CAD, DAB: these three shall be together less than four right angles.
 In the straight lines AB,AC,AD take any points B, C,D, and join BC, CD, DB.
In the straight lines AB,AC,AD take any points B, C,D, and join BC, CD, DB.
Then, because the solid angle at B is contained by the three plane angles CBA, ABD, DBC, any two of them are together greater than the third, [XI. 20.
therefore the angles CBA, ABD are together greater than the angle DBC.
For the same reason, the angles BCA, ACD are together greater than the angle DCB,
and the angles CDA, ADB are together greater than the angle BDC.
Therefore the six angles CBA, ABD, BCA, ACD, CDA, ADB are together greater than the three angles DBC, DCB, BDC;
but the three angles DBC, DCB, BDC are together equal to two right angles. [I. 32.
Therefore the six angles CBA, ABD, BCA, ACD, CDA, ADB are together greater than two right angles.
And, because the three angles of each of the triangles ABC, ACD, ADB are together equal to two right angles, [1. 32.
therefore the nine angles of these triangles, namely, the angles CBA, BAC, ACB, ACD,CDA, CAD, ADD, DBA, DAB are equal to six right angles;
and of these, the six angles CBA, ACB, ACD, CDA, ADB, DBA are greater than two right angles,
therefore the remaining three angles BAC, CAD, DAB, which contain the solid angle at A, are together less than four right angles.
Next, let the solid angle at A be contained by any number of plane angles BAC, CAD, DAE, EAF, FAB: these shall be together less than four right angles.
 Let the planes in which the angles are, be cut by a plane, and let the common sections of it with those planes be BC, CD, DE, EF, FB.
Let the planes in which the angles are, be cut by a plane, and let the common sections of it with those planes be BC, CD, DE, EF, FB.
Then, because the solid angle at B is contained by the three plane angles CBA, ABF, FBC, any two of them are together greater than the third, [XL 20.
therefore the angles CBA, ABF are together greater than the angle FBC.
For the same reason, at each of the points C, D, E, F, the two plane angles which are at the bases of the triangles having the common vertex A, are together greater than the third angle at the same point, which is one of the angles of the polygon BCDEF.
Therefore all the angles at the bases of the triangles are together greater than all the angles of the polygon.
Now all the angles of the triangles are together equal to twice as many right angles as there are triangles, that is, as there are sides in the polygon BCDEF; [I. 32.
and all the angles of the polygon, together with four right angles, are also equal to twice as many right angles as there are sides in the polygon; [I. 32, Corollary 1.
therefore all the angles of the triangles are equal to all the angles of the polygon, together with four right angles. [Ax. 1.
But it has been shewn that all the angles at the bases of the triangles are together greater than all the angles of the polygon;
therefore the remaining angles of the triangles, namely, those at the vertex, which contain the solid angle at A, are together less than four right angles.
Wherefore, every solid angle &c. q.e.d.