Translation:The Sagnac Effect: An Experimentum Crucis in Favor of the Aether?
The Sagnac Effect:
An Experimentum Crucis in Favor of the Aether?
by Hans Witte.
(Received January 19, 1914.)
1. The common fundamental idea of the optical experiments aimed at bringing a decision to the question of the existence or non-existence of the aether, and which were actually executed or imagined as executed, is as follows:
If there is an aether, then the optical processes in all systems moving relative to the aether, must proceed in a deviating way; especially, a different value of the speed of light than the standard value must be measured in all such systems.
The amount of change to be expected is determined (besides the direction of motion) by the magnitude of the relative velocity of the system relative to the aether (or when viewed oppositely, by the velocity of the relative "aether stream" or "aether wind").
The largest relative velocities, which had been accounted for by now, are of order of magnitude 30 km/sec, thus the expected result is given by the ratio = ca. .
Yet, until now we were of the conviction, that an effect of this order of magnitude, i.e., of the first order, cannot be measured mainly due to the fact, that it would require observations at two different points of the system.
Thus the decision was relegated to effects of second order (thus in the best case = ca. ). Already Maxwell showed, that terms of second order should be demonstrated by measurement at one and the same point; the experiment of Michelson became the experimentum crucis.
It was mainly the negative result of this experiment, which finally led many physicists, especially the proponents of the recent relativity principle, to the abandonment of the aether.
2. Now, Sagnac[1] has recently provided a new optical effect for deciding the aether question.
Remarkably, this effect is of first order; nevertheless all measurements take place in one and the same point of the system.
The Effect can very well be observed also at small translatory velocities by means of interference phenomena, which was actually done by Sagnac.

The effect was demonstrated indeed. Order of magnitude and sense of displacement were in agreement, and additionally, the observed fringe displacements were even in terms of numbers in noticeable good agreement with the calculated ones.
Sagnac thus concludes from theory and experiment:[2] The fringe displacement measures the relative velocity of the system with respect to the aether (or the relative aether wind, vent relatif de l’éther), thus is proves the existence of the aether.
3. The work of Sagnac is therefore of very great importance.
Now, I'm not in the least thinking about casting doubt on the experimental part of the work, on the contrary, I consider the method itself of being capable to be further developed in different directions.
On the other hand, the theoretical foundations and consequently also the conclusions, not necessarily require the interpretation given by Sagnac.
4. I allow myself, to reproduce the basic idea of the experimental arrangement in a somewhat schematic form, with the note that the state of matter itself is not changed by that.
A sphere of radius shall be given (Fig. 1), which is reflecting at the interior side.
At one point of the rim, a light ray is split; part is circulating clockwise, the other part counter-clockwise.
 |
 |
Both parts follow the same polygon which is closed by one circulation (an octagon in Fig. 1)
If denotes the circumference of the polygon, then the same is thus the light path for both rays; the circulating time is:
,
both rays simultaneously arrive in again.
Now we think of observation point as having the translatory velocity ; namely this shall happen by rotating the circle with rotating number , thus it shall be:
Equally well[3], one also can think of point and the whole circle as being held at rest, then at every location as well as at any boundary point of the circle there is a oppositely directed aether wind (vent relatif de l’éther) of same absolute amount
| 1) |
of relative aether velocity.
The imagined rotation of the system shall happen counter-clockwise ()
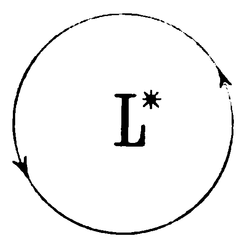
thus the relative aether circulates clockwise () in relation to the system imagined as being at rest.

Of the two light rays denoted by and , which are circulating clockwise and counter-clockwise, one (namely ray ) at first travels faster away from , then in the same measure faster around the whole circle, and also faster back to point ; the other one, , is held back in the same way. –
When any wave is transmitted faster or held back by a relative stream of the wave-carrying medium, then it's known that (in first approximation), the time of earliness or delay is defined – with respect to normal time employed at standard velocity – by
,
in case the directions of and coincide or are precisely opposite; instead of time one can also introduce the (apparent) path-contraction or -elongations , then is defined – with respect to the normal path ("real" path) – by
| 2) |
and the phase change at wavelength , is given by:
| 3) |
This formula is also to be applied in our case, it must only be considered that the direction of the translatory velocity (tangent)

and that of light (polygon side) do not coincide, it is thus (as it follows from Fig. 2) substituted instead of :
where denotes the polygon side of the corresponding central-angle.
If one substitutes this value, than the phase difference , mutually experienced by rays and due to the relative aether stream, is:
| 4) |
Finally one can substitute value 1) for velocity of the relative aether stream with rotating number and circle radius , then it is given:
| 5) |
Due to reasons of measurement, Sagnac causes the apparatus to turn in one sense first, then in the other sense, thus he measures , and his end formula[4] therefore reads:
| 6) |
By this formula 6), Sagnac calculates the fringe displacement to be expected; that the effect is indeed of first order shows variation 4) of the same formula.
As it was said, then the observed value agrees quite satisfactorily with the calculated one.
The circle diameter amounts to 50 cm; the rotating number is of order of magnitude 1 or 2 rotations per second; the interference images are made in a photographic way; the photographic plate, the light source, etc., share the rotation.
5. It is now the question, whether Sagnac's conclusion that the effect is deciding the alternative "aether or relativity principle", namely that it decides against the relativity principle and in favor of the aether, is necessary.[5]
The following representation seems possible to me:
a) That the effect comes about, doesn't follow from the translatory velocity of observing point , but from the rotational motion of the whole system (and by that of course also point ).
Yet, because the effect is caused by rotation, its occurrence is a necessary postulate not only from the standpoint of the aether theories, but equally well also from the anti-aether standpoint.
c) Thus this effect doesn't prove the aether.
6. The correctness of assertion a) follows without further ado, by thinking of the system as having a rectilinear uniform translation instead of the rotation process.[6] Then the effect is missing.
I omit the prove (which is in general easily given) because a remark by Sagnac himself in an older work[7] seems to speak for the fact, that his view doesn't contradict that of mine in this point.

7. Also with respect to assertion b), a schematizing sketch shall suffice:
First it is easily given: The occurrence of the effect is also then a necessary postulate, when one considers the process during the rotation, not in the way of § 4 (rotating disc thought as at rest, relative aether wind all around), but from the standpoint of the previously resting system (aether "at rest", while the disc is rotating).
Fig. 3 serves to illustrate this: The polygon shall be (in the stationary process) a closed square, for light ray and for light ray ; be the arc followed by point during the normal light circulation , when the apparatus is rotating as above (arrow direction ). In this view, a real contraction occurs for light path , and for light path a real elongation, since the light paths are in the same approximation as above and . If one computes the phase displacement, then the same amount is given as above (formula 6).
Furthermore, the same is given in a familiar way from the standpoint of the anti-aether theory (relativity principle)[8], one only has to replace the word aether by the word "one inertial system".
Thus this effect must be demanded also from the standpoint of the relativity principle, namely the cause for its realization is, that the apparatus is rotating relative to an "inertial system", and that (seen from an inertial system) an objective contraction or elongation of first order arise in the total light paths.
The same conclusions then naturally also hold (from the standpoint of relativity) for any inertial system.[9]
8. Consequently, also assertion c) is correct: The effect doesn't prove the aether.
The rotating relative aether wind of § 4 shall not be used at all from the anti-aether standpoint; the rotating system is, in the sense of the terminology of relativity, no "valid" system at all, i.e., nobody can of course be prohibited to illustrate the actually arising effect by a "relative aether wind", but this is only an image from the standpoint of relativity, like "the sun is rising".
For the decision "aether or non-aether?", all rotating systems are failing according to the relativity-theoretical view. The existence of the aether is proven, as soon as the following is proven: an inertial system is preferred over another inertial system; thus as soon as one – in the comparison of inertial frames among each other – finds an "effect" of the discussed or of similar kind. On the other hand, every inertial system is preferred over rotating systems from the relativity standpoint, and vice versa; when inertial- are compared with rotational systems, or rotational system are mutually compared, one therefore must always find some "effects".
Braunschweig, Technische Hochschule, January 1914.
- ↑ G. Sagnac, L’éther lumineux démontré par l’effet du vent relatif d’éther, C. R. 157, 708, 27. October 1913; Sur la preuve de la réalité de l’éther lumineux, same place p. 1410, 22. December 1913.
- ↑ A. a. 0., S. 710 u. 1413.
- ↑ G. Sagnac, l.c., p. 709 u. 1411.
- ↑ A. a. O., S. 710 u. 1412.
- ↑ Only this alternative is discussed by me in the following. Regarding another important alternative, namely "emission- or non-emission theory", this effect very much seems to me as capable of being used as an experimentum crucis (against the emission theories), then it is a very valuable terrestrial counterpart of the known astronomical verifications.
- ↑ For example that one (changing continuously), which is approximately executed by point individually at every moment (in the direction of the circle tangent, the velocity is as given above).
- ↑ G. Sagnac, Congrès International de Radiologie et d’Électricité, p. 221, Brussels 1911.
- ↑ It is to be considered, that the relevant translatory velocity of the mirrors lies in the mirror plane. A potential influence of a possible temporal duration of the reflection process itself, is of course neglected (as it was also done by Sagnac). My conclusions are also based on the assumption, that the often disputed process of rotation of a rigid system as such, constitutes no problem for the relativity principle.
- ↑ For example, also for that one (changing continuously), in which point is present at every moment (in the direction of the circle tangent, the velocity relative to the "rest"-inertial system is as given above).
![]()
![]() This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
| Original: |
This work is in the public domain in the United States because it was published before January 1, 1929. The longest-living author of this work died in 1925, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 98 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
Public domainPublic domainfalsefalse |
|---|---|
| Translation: |
This work is released under the Creative Commons Attribution-ShareAlike 3.0 Unported license, which allows free use, distribution, and creation of derivatives, so long as the license is unchanged and clearly noted, and the original author is attributed.
Public domainPublic domainfalsefalse |















































