A Dictionary of Music and Musicians/Tuning
TUNING (To tune; Fr. accorder; Ital. accordare; Germ, stimmeri). The adjustment to a recognised scale of any musical instrument capable of alteration in the pitch of the notes composing it. The violin family, the harp, piano, organ, and harmonium, are examples of instruments capable of being tuned. The accordance of the violin, viola, and violoncello, as is well known, is in fifths which are tuned by the player.[1] The harpist also tunes his harp. But the tuning of the piano, organ, and harmonium, is effected by tuners who acquire their art, in the piano especially, by long practice, and adopt tuning, particularly in this country, as an independent calling, having little to do with the mechanical processes of making the instrument. At Antwerp, as early as the first half of the 17th century, there were harpsichord-tuners who were employed in that vocation only; for instance, in De Liggeren der Antwerpsche Sint Lucasgilde, p. 24, edited by Rombouts and Van Lerius (the Hague) we find named as a master Michiel Colyns, Claversingelstelder Wynmeester, i.e. harpsichord-tuner and son of a master (in modern Flemish Clavecimbel-steller).
In all keyboard instruments the chief difficulty has been found in what is known as 'laying the scale, bearings, or groundwork,' of the tuning; an adjustment of a portion of the compass, at most equal in extent to the stave with the Alto clefFor the Naturals (das gelbe Clavier).

For the Sharps (Obertasten).
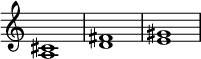
must be Major Thirds (mussen grosse Terzen sein).

are Minor Thirds (tiefer erklingen).
There is not a word about temperament!
By the stave for the naturals we may restore the tuning of the Guido scale of the earliest organs and clavichords which had only the B♭ as an upper key in two octaves. These would be provided for either by tuning up from the G (a minor third) or down from the F (a fifth), all the intervals employed being approximately just. We may also suppose that from the introduction of the full chromatic scale in organs before 1426, to the date of Schlick's publication 1511, and indeed afterwards, such a groundwork as Ammerbach's may have sufficed. There was a difference in clavichords arising from the fretting, to which we will refer later. Now, in 1511, Arnolt Schlick, a blind organist alluded to by Virdung, in his 'Spiegel der Orgelmacher' (Mirror of Organbuilders)—a work which the present writer, aided by its republication in Berlin in 1869, has brought under the notice of writers on music—came out as a reformer of tuning. He had combatted the utter subordination of the sharps or upper keys to the natural notes, and by the invention of a system of tuning of fifths and octaves had introduced a groundwork which afforded a kind of rough-and-ready unequal temperament and gave the sharps a quasi independence. This is his scale which he gives out for organs, clavicymbals, clavichords, lutes, harps, intending it for wherever it could be applied.

He gives directions that ascending fifths should be made flat to accommodate the major thirds, particularly F—A, G—B♮, and C—E,—excepting G♯, which should be so tuned to E♭, as to get a tolerable cadence or dominant chord, the common chord of E, to A. The G♯ to the E♭, he calls the 'wolf,' and says it is not used as a dominant chord to cadence C♯. Indeed, from the dissonance attending the use of C♯ and A♭, they being also out of tune with each other, he recommends the player to avoid using them as keynotes, by the artifice of transposition.
The fact of Ammerbach's publication of the older groundwork 60 years later proves that Schlick's was slow to commend itself to practice. However, we find Schlick's principle adopted and published by Mersenne (Hannonie Universelle, Paris, 1636) and it was doubtless by that time established to the exclusion of the earlier system. With this groundwork Mersenne adopted, at least in theory, Equal Temperament [see Temperament], of which in Liv. 2, Prop. xi. p. 132, of the before-named work, he gives the correct figures, and in the next volume, Prop. xii, goes on to say that equal temperament is the most used and the most convenient, and that all practical musicians allow that the division of the octave into twelve half-tones is the easiest for performance. Mr. Ellis, in his exhaustive Lecture on the History of Musical Pitch (Journal of the Society of Arts, Appendix of April 2, 1880), considers corroboration of this statement necessary. We certainly do not find it in Mersenne's notation of the tuning scale which we here transpose from the baritone clef.

Les Feintes. The Sharps and Flats.

For the tuner's guidance the ascending fifths are marked as flat, the descending as sharp, but the last fifth, G♯—E♭, is excepted as being the 'defect of the accord.' With this recognition of the 'wolf' it is clear that Mersenne was not thinking of equal temperament. But Schlick's principle of fifths and octaves had become paramount.
We will now go back to the interesting 'gebunden' or fretted clavichord. [See Clavichord and Tangent.] The octave open scale of this instrument is F G A B♭ C D E♭ F, or C D E♭ F G A B♭ C, according to the note which may be accepted as the starting-point. Both of these are analogous to church modes, but may be taken as favourite popular scales, before harmony had fixed the present major and minor, and the feeling had arisen for the leading note. We derive the fretted clavichord tuning from Ammerbach thus:

Later on, no doubt, four fifths up, F C G D A and two fifths down F B♭ E♭, would be used with octaves inserted to keep the tuning for the groundwork, in the best part of the keyboard for hearing. We have found the fretted or stopped semitones which included the natural B and E, adjusted by a kind of rough temperament, intended to give equal semi mean-tones and resembling the lute and guitar semitones.
When J. Sebastian Bach had under his hands the 'bundfrei' or fret-free clavichord, each key having its own strings, he could adopt the tuning by which he might compose in all the twenty-four keys, from which we have the 48 Preludes and Fugues.[2]
Emanuel Bach ('Versuch,' etc., Berlin 1753) gives, p. 10, very clear testimony as to his own preference for equal temperament tuning. He says we can go farther with this new kind of tuning although the old kind had chords better than could be found in musical instruments generally. He does not allude to his father, but brings in a hitherto unused interval in keyboard instrument tuning—the Fourth. Not, it is true, in place of the Fifth; but as one of the trials to test the accuracy of the tuning. At the present time beginners in tuning find the Fourth a difficult interval when struck simultaneously with the note to which it makes the interval: there is a feeling of dissonance not at all perceptible in the Fifth. It is therefore not strange that for centuries we do not find it used for instruments capable of more or less sustained harmony. The introduction of a short groundwork for the piano, confined to the simple chromatic scale between
—the wolf being, as of old, at the meeting of G♯ and E♭. The advantages of the short system were in the greater resemblance of vibration between notes so near, and the facilities offered for using common chords as trials. It will be observed that the pitch-note has changed from F to the treble C; possibly from the introduction of the Tuning-fork in 1711. In Great Britain and Italy a C-fork has been nearly always adhered to since that date for keyboard instruments; but for the violins, A (on account of the violin open string), which in France and Germany has been also adopted as the keyboard tuning-note. But the pitchpipe may have also had to do with the change of pitch-note.
The long tuning scale did not at once go out of use; it was adhered to for organs, and for pianos by tuners of the old school. It went out in Messrs. Broadwood's establishment with the last tuner who used it, about the year 1869. The change to intentional equal temperament in pianos in 1846, in England, which preceded by some years the change in the organ, was ushered in by an inclination to sharper major thirds: examples differing as different tuners were inclined to more or less 'sweet' common chords of C, G, and F. The wolf ceasing to howl so loudly, another short groundwork, which went through the chain of fourths and fifths without break, became by degrees more general with the piano until it prevailed entirely. It is as follows:

and is also the groundwork for tuning the harmonium.
The organ no longer remains with the groundwork of fifths and octaves; the modern tuners use fourths and fifths in the treble C—C, of the Principal; entirely disregarding the thirds. Like the harmonium the organ is tuned entirely by beats. Organ pipes are tuned by cutting them down shorter, or piecing them out longer, when much alteration has to be made. When they are nearly of the right pitch, (1) metal pipes are 'coned in' by putting on and pressing down the 'tuning horn,' to turn the edges in for flattening, or 'coned out' by inserting and pressing down the tuning horn to turn the edges out for sharpening; (2) stopped pipes, wooden or metal, are sharpened by screwing or pushing the stopper down, or flattened by pulling it up; (3) reed pipes by a tuning wire which lengthens or shortens the vibrating portion of the tongue. Harmoniums are tuned by scraping the metal tongue of the reed near the free end to sharpen the tone, and near the attached end to flatten it.
The old way of tuning pianos by the Tuning Hammer (or a Tuning Lever) remains in vogue, notwithstanding the ever-recurring attempts to introduce mechanical contrivances of screws etc., which profess to make tuning easy and to bring it more or less within the immediate control of the player. Feasible as such an improvement appears to be, it has not yet come into the domain of the practical. The co-ordination of hand and ear, possessed by a skilled tuner, still prevails, and the difficulty of getting the wire to pass over the bridge, continuously and equally without the governed strain of the tuner's hand, is still to be overcome before a mechanical system can rival a tuner's dexterity.
In considering practical tuning we must at once dismiss the idea that the ear of a musician is capable of distinguishing small fractions of a complete vibration in a second. Professor Preyer of Jena limits the power of perception of the difference of pitch of two notes heard in succession by the best ears to about one third of a double vibration in a second in any part of the scale. By the phenomena of beats between two notes heard at the same time we can make much finer distinctions, which are of great use in tuning the organ and harmonium; but with the piano we may not entirely depend upon them, and a good musical ear for melodic succession has the advantage. In fact the rapid beats of the upper partial tones frequently prevent the recognition of the slower beats of the fundamental tones of the notes themselves until they become too faint to count by. The tuner also finds difficulty in tuning the treble of a piano by beats only.
Still, to tune the groundwork of a piano to a carefully measured set of chromatic tuning forks, such as Scheibler formerly provided, would ensure a nearer approach to a perfect equal temperament than the existing system of fourths and fifths, with the slight flattening upwards of fifths and downwards of fourths, to bring all within the perfect octave. But to achieve this, a normal pitch admitting of no variation is a sine quâ non, because no tuner would or could give the time to work by a set of forks making beats with the pitch wanted.
The wind and fretted stringed instruments, although seemingly of fixed tones, are yet capable of modification by the player, and their exact scale relation cannot be defined without him. In Asiatic countries, as India, Persia, and Arabia, and sometimes in European, this play of interval is used as a melodic grace, and from the ancient Greeks to the present day, the quarter-tone has been a recognised means of expression. Georges Sand, writing in her delightful novel 'La Mare au Diable' about the Musette (a kind of Bagpipe) of her country people, says—'La note finale de chaque phrase, tenue et tremblée avec une longueur et une puissance d'haleine incroyable, monte d'un quart de ton en faussant systématiquement.' Whitley Stokes (Life of Dr. Petrie, p. 339) has noticed such a licence in his native Irish music. But we are led away here from Harmonic Scales.[ A. J. H. ]
- ↑ The accordances of the guitar, lute, theorbo, and similar instruments tuned by fifths, fourths, and thirds will be found in the descriptions of them.
- ↑ He did not get this tuning on the organ, It would appear, although his preference for it is shown in Mr. Ellis's 'History of Musical Pitch' already referred to. (See the 'Journal of the Society of Arts,' March 5, 1860).