A Treatise on Electricity and Magnetism/Part IV/Chapter III
CHAPTER III.
ON THE INDUCTION OF ELECTRIC CURRENTS.
528.] The discovery by Örsted of the magnetic action of an electric current led by a direct process of reasoning to that of magnetization by electric currents, and of the mechanical action between electric currents. It was not, however, till 1831 that Faraday, who had been for some time endeavouring to produce electric currents by magnetic or electric action, discovered the conditions of magneto-electric induction. The method which Faraday employed in his researches consisted in a constant appeal to experiment as a means of testing the truth of his ideas, and a constant cultivation of ideas under the direct influence of experiment. In his published researches we find these ideas expressed in language which is all the better fitted for a nascent science, because it is somewhat alien from the style of physicists who have been accustomed to established mathematical forms of thought.
The experimental investigation by which Ampère established the laws of the mechanical action between electric currents is one of the most brilliant achievements in science.
The whole, theory and experiment, seems as if it had leaped, full grown and full armed, from the brain of the 'Newton of electricity. It is perfect in form, and unassailable in accuracy, and it is summed up in a formula from which all the phenomena may be deduced, and which must always remain the cardinal formula of electro-dynamics.
The method of Ampère, however, though cast into an inductive form, does not allow us to trace the formation of the ideas which guided it. We can scarcely believe that Ampère really discovered the law of action by means of the experiments which he describes. We are led to suspect, what, indeed, he tells us himself[1], that he discovered the law by some process which he has not shewn us, and that when he had afterwards built up a perfect demonstration he removed all traces of the scaffolding by which he had raised it.
Faraday, on the other hand, shews us his unsuccessful as well as his successful experiments, and his crude ideas as well as his developed ones, and the reader, however inferior to him in inductive power, feels sympathy even more than admiration, and is tempted to believe that, if he had the opportunity, he too would be a discoverer. Every student therefore should read Ampère's research as a splendid example of scientific style in the statement of a discovery, but he should also study Faraday for the cultivation of a scientific spirit, by means of the action and reaction which will take place between newly discovered facts and nascent ideas in his own mind.
It was perhaps for the advantage of science that Faraday, though thoroughly conscious of the fundamental forms of space, time, and force, was not a professed mathematician. He was not tempted to enter into the many interesting researches in pure mathematics which his discoveries would have suggested if they had been exhibited in a mathematical form, and he did not feel called upon either to force his results into a shape acceptable to the mathematical taste of the time, or to express them in a form which mathematicians might attack. He was thus left at leisure to do his proper work, to coordinate his ideas with his facts, and to express them in natural, untechnical language.
It is mainly with the hope of making these ideas the basis of a mathematical method that I have undertaken this treatise.
529.] We are accustomed to consider the universe as made up of parts, and mathematicians usually begin by considering a single particle, and then conceiving its relation to another particle, and so on. This has generally been supposed the most natural method. To conceive of a particle, however, requires a process of abstraction, since all our perceptions are related to extended bodies, so that the idea of the all that is in our consciousness at a given instant is perhaps as primitive an idea as that of any individual thing. Hence there may be a mathematical method in which we proceed from the whole to the parts instead of from the parts to the whole. For example, Euclid, in his first book, conceives a line as traced out by a point, a surface as swept out by a line, and a solid as generated by a surface. But he also defines a surface as the boundary of a solid, a line as the edge of a surface, and a point as the extremity of a line.
In like manner we may conceive the potential of a material system as a function found by a certain process of integration with respect to the masses of the bodies in the field, or we may suppose these masses themselves to have no other mathematical meaning than the volume-integrals of where is the potential.
In electrical investigations we may use formulae in which the quantities involved are the distances of certain bodies, and the electrifications or currents in these bodies, or we may use formulae which involve other quantities, each of which is continuous through all space.
The mathematical process employed in the first method is integration along lines, over surfaces, and throughout finite spaces, those employed in the second method are partial differential equations and integrations throughout all space.
The method of Faraday seems to be intimately related to the second of these modes of treatment. He never considers bodies as existing with nothing between them but their distance, and acting on one another according to some function of that distance. He conceives all space as a field of force, the lines of force being in general curved, and those due to any body extending from it on all sides, their directions being modified by the presence of other bodies. He even speaks[2] of the lines of force belonging to a body as in some sense part of itself, so that in its action on distant bodies it cannot be said to act where it is not. This, however, is not a dominant idea with Faraday. I think he would rather have said that the field of space is full of lines of force, whose arrangement depends on that of the bodies in the field, and that the mechanical and electrical action on each body is determined by the lines which abut on it.
PHENOMENA OF MAGNETO-ELECTRIC INDUCTION[3].
Let there be two conducting circuits, the Primary and the Secondary circuit. The primary circuit is connected with a voltaic battery by which the primary current may be produced, maintained, stopped, or reversed. The secondary circuit includes a galvanometer to indicate any currents which may be formed in it. This galvanometer is placed at such a distance from all parts of the primary circuit that the primary current has no sensible direct influence on its indications.
Let part of the primary circuit consist of a straight wire, and part of the secondary circuit of a straight wire near, and parallel to the first, the other parts of the circuits being at a greater distance from each other.
It is found that at the instant of sending a current through the straight wire of the primary circuit the galvanometer of the secondary circuit indicates a current in the secondary straight wire in the opposite direction. This is called the induced current. If the primary current is maintained constant, the induced current soon disappears, and the primary current appears to produce no effect on the secondary circuit. If now the primary current is stopped, a secondary current is observed, which is in the same direction as the primary current. Every variation of the primary current produces electromotive force in the secondary circuit. When the primary current increases, the electromotive force is in the opposite direction to the current. When it diminishes, the electromotive force is in the same direction as the current. When the primary current is constant, there is no electromotive force.
These effects of induction are increased by bringing the two wires nearer together. They are also increased by forming them into two circular or spiral coils placed close together, and still more by placing an iron rod or a bundle of iron wires inside the coils.
2. Induction by Motion of the Primary Circuit.
We have seen that when the primary current is maintained constant and at rest the secondary current rapidly disappears.
Now let the primary current be maintained constant, but let the primary straight wire be made to approach the secondary straight wire. During the approach there will be a secondary current in the opposite direction from the primary.
If the primary circuit be moved away from the secondary, there will be a secondary current in the same direction as the primary.
3. Induction by Motion of the Secondary Circuit.
If the secondary circuit be moved, the secondary current is opposite to the primary when the secondary wire is approaching the primary wire, and in the same direction when it is receding from it.
In all cases the direction of the secondary current is such that the mechanical action between the two conductors is opposite to the direction of motion, being a repulsion when the wires are approaching, and an attraction when they are receding. This very important fact was established by Lenz[4].
4. Induction by the Relative Motion of a Magnet and the Secondary Circuit.
If we substitute for the primary circuit a magnetic shell, whose edge coincides with the circuit, whose strength is numerically equal to that of the current in the circuit, and whose austral face corresponds to the positive face of the circuit, then the phenomena produced by the relative motion of this shell and the secondary circuit are the same as those observed in the case of the primary circuit.
531.] The whole of these phenomena may be summed up in one law. When the number of lines of magnetic induction which pass through the secondary circuit in the positive direction is altered, an electromotive force acts round the circuit, which is measured by the rate of decrease of the magnetic induction through the circuit.
532.] For instance, let the rails of a railway be insulated from the earth, but connected at one terminus through a galvanometer, and let the circuit be completed by the wheels and axle of a railway carriage at a distance from the terminus. Neglecting the height of the axle above the level of the rails, the induction through the secondary circuit is due to the vertical component of the earth's magnetic force, which in northern latitudes is directed downwards. Hence, if is the gauge of the railway, the horizontal area of the circuit is , and the surface-integral of the magnetic induction through it is , where is the vertical component of the magnetic force of the earth. Since is downwards, the lower face of the circuit is to be reckoned positive, and the positive direction of the circuit itself is north, east, south, west, that is, in the direction of the sun's apparent diurnal course.
Now let the carriage be set in motion, then will vary, and there will be an electromotive force in the circuit whose value .
If is increasing, that is, if the carriage is moving away from the terminus, this electromotive force is in the negative direction, or north, west, south, east. Hence the direction of this force through the axle is from right to left. If were diminishing, the absolute direction of the force would be reversed, but since the direction of the motion of the carriage is also reversed, the electromotive force on the axle is still from right to left, the observer in the carriage being always supposed to move face forwards. In southern latitudes, where the south end of the needle dips, the electromotive force on a moving body is from left to right.
Hence we have the following rule for determining the electromotive force on a wire moving through a field of magnetic force. Place, in imagination, your head and feet in the position occupied by the ends of a compass needle which point north and south respectively; turn your face in the forward direction of motion, then the electromotive force due to the motion will be from left to right.
533.] As these directional relations are important, let us take another illustration. Suppose a metal girdle laid round the earth at the equator, and a metal wire laid along the meridian of Greenwich from the equator to the north pole.

Fig. 31.
Let a great quadrantal arch of metal be constructed, of which one extremity is pivoted on the north pole, while the other is carried round the equator, sliding on the great girdle of the earth, and following the sun in his daily course. There will then be an electromotive force along the moving quadrant, acting from the pole towards the equator.
The electromotive force will be the same whether we suppose the earth at rest and the quadrant moved from east to west, or whether we suppose the quadrant at rest and the earth turned from west to east. If we suppose the earth to rotate, the electromotive force will be the same whatever be the form of the part of the circuit fixed in space of which one end touches one of the poles and the other the equator. The current in this part of the circuit is from the pole to the equator.
The other part of the circuit, which is fixed with respect to the earth, may also be of any form, and either within or without the earth. In this part the current is from the equator to either pole.
534.] The intensity of the electromotive force of magneto-electric induction is entirely independent of the nature of the substance of the conductor in which it acts, and also of the nature of the conductor which carries the inducing current.
To shew this, Faraday[5] made a conductor of two wires of different metals insulated from one another by a silk covering, but twisted together, and soldered together at one end. The other ends of the wires were connected with a galvanometer. In this way the wires were similarly situated with respect to the primary circuit, but if the electromotive force were stronger in the one wire than in the other it would produce a current which would be indicated by the galvanometer. He found, however, that such a combination may be exposed to the most powerful electromotive forces due to induction without the galvanometer being affected. He also found that whether the two branches of the compound conductor consisted of two metals, or of a metal and an electrolyte, the galvanometer was not affected[6].
Hence the electromotive force on any conductor depends only on the form and the motion of that conductor, together with the strength, form, and motion of the electric currents in the field.
535.] Another negative property of electromotive force is that it has of itself no tendency to cause the mechanical motion of any body, but only to cause a current of electricity within it.
If it actually produces a current in the body, there will be mechanical action due to that current, but if we prevent the current from being formed, there will be no mechanical action on the body itself. If the body is electrified, however, the electromotive force will move the body, as we have described in Electrostatics.
536.] The experimental investigation of the laws of the induction of electric currents in fixed circuits may be conducted with considerable accuracy by methods in which the electromotive force, and therefore the current, in the galvanometer circuit is rendered zero.
For instance, if we wish to shew that the induction of the coil on the coil is equal to that of upon , we place the first pair of coils and at a sufficient distance from the second pair
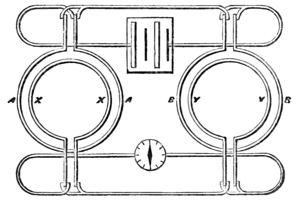
Fig. 32.
and . We then connect and with a voltaic battery, so that we can make the same primary current flow through in the positive direction and then through in the negative direction. We also connect and with a galvanometer, so that the secondary current, if it exists, shall flow in the same direction through and in series.
Then, if the induction of on is equal to that of on , the galvanometer will indicate no induction current when the battery circuit is closed or broken.
The accuracy of this method increases with the strength of the primary current and the sensitiveness of the galvanometer to instantaneous currents, and the experiments are much more easily performed than those relating to electromagnetic attractions, where the conductor itself has to be delicately suspended.
A very instructive series of well devised experiments of this kind is described by Professor Felici of Pisa[7].
I shall only indicate briefly some of the laws which may be proved in this way.
(1) The electromotive force of the induction of one circuit on another is independent of the area of the section of the conductors and of the material of which they are made.
For we can exchange any one of the circuits in the experiment for another of a different section and material, but of the same form, without altering the result.
(2) The induction of the circuit on the circuit is equal to that of upon .
For if we put in the galvanometer circuit, and in the battery circuit, the equilibrium of electromotive force is not disturbed.
(3) The induction is proportional to the inducing current.
For if we have ascertained that the induction of on is equal to that of on , and also to that of on , we may make the battery current first flow through , and then divide itself in any proportion between and . Then if we connect reversed, and direct, all in series, with the galvanometer, the electromotive force in will balance the sum of the electromotive forces in and .
(4) In pairs of circuits forming systems geometrically similar the induction is proportional to their linear dimensions.
For if the three pairs of circuits above mentioned are all similar, but if the linear dimension of the first pair is the sum of the corresponding linear dimensions of the second and third pairs, then, if , , and are connected in series with the battery, and reversed, and also in series with the galvanometer, there will be equilibrium.
(5) The electromotive force produced in a coil of windings by a current in a coil of windings is proportional to the product .
537.] For experiments of the kind we have been considering the galvanometer should be as sensitive as possible, and its needle as light as possible, so as to give a sensible indication of a very small transient current. The experiments on induction due to motion require the needle to have a somewhat longer period of vibration, so that there may be time to effect certain motions of the conductors while the needle is not far from its position of equilibrium. In the former experiments, the electromotive forces in the galvanometer circuit were in equilibrium during the whole time, so that no current passed through the galvanometer coil. In those now to be described, the electromotive forces act first in one direction and then in the other, so as to produce in succession two currents in opposite directions through the galvanometer, and we have to shew that the impulses on the galvanometer needle due to these successive currents are in certain cases equal and opposite.
The theory of the application of the galvanometer to the measurement of transient currents will be considered more at length in Art. 748. At present it is sufficient for our purpose to observe that as long as the galvanometer needle is near its position of equilibrium the deflecting- force of the current is proportional to the current itself, and if the whole time of action of the current is small compared with the period of vibration of the needle, the final velocity of the magnet will be proportional to the total quantity of electricity in the current. Hence, if two currents pass in rapid succession, conveying equal quantities of electricity in opposite directions, the needle will be left without any final velocity.
Thus, to shew that the induction-currents in the secondary circuit, due to the closing and the breaking of the primary circuit, are equal in total quantity but opposite in direction, we may arrange the primary circuit in connexion with the battery, so that by touching a key the current may be sent through the primary circuit, or by removing the finger the contact may be broken at pleasure. If the key is pressed down for some tune, the galvanometer in the secondary circuit indicates, at the time of making contact, a transient current in the opposite direction to the primary current. If contact be maintained, the induction current simply passes and disappears. If we now break contact, another transient current passes in the opposite direction through the secondary circuit, and the galvanometer needle receives an impulse in the opposite direction.
But if we make contact only for an instant, and then break contact, the two induced currents pass through the galvanometer in such rapid succession that the needle, when acted on by the first current, has not time to move a sensible distance from its position of equilibrium before it is stopped by the second, and, on account of the exact equality between the quantities of these transient currents, the needle is stopped dead.
If the needle is watched carefully, it appears to be jerked suddenly from one position of rest to another position of rest very near the first.
In this way we prove that the quantity of electricity in the induction current, when contact is broken, is exactly equal and opposite to that in the induction current when contact is made.
538.] Another application of this method is the following, which is given by Felici in the second series of his Researches.
It is always possible to find many different positions of the secondary coil , such that the making or the breaking of contact in the primary coil produces no induction current in . The positions of the two coils are in such cases said to be conjugate to each other.
Let and be two of these positions. If the coil be suddenly moved from the position to the position , the algebraical sum of the transient currents in the coil is exactly zero, so that the galvanometer needle is left at rest when the motion of is completed.
This is true in whatever way the coil is moved from to , and also whether the current in the primary coil be continued constant, or made to vary during the motion.
Again, let be any other position of not conjugate to , so that the making or breaking of contact in produces an induction current when is in the position .
Let the contact be made when is in the conjugate position , there will be no induction current. Move to , there will be an induction current due to the motion, but if is moved rapidly to , and the primary contact then broken, the induction current due to breaking contact will exactly annul the effect of that due to the motion, so that the galvanometer needle will be left at rest. Hence the current due to the motion from a conjugate position to any other position is equal and opposite to the current due to breaking contact in the latter position.
Since the effect of making contact is equal and opposite to that of breaking it, it follows that the effect of making contact when the coil is in any position is equal to that of bringing the coil from any conjugate position to while the current is flowing through .
If the change of the relative position of the coils is made by moving the primary circuit instead of the secondary, the result is found to be the same.
539.] It follows from these experiments that the total induction current in during the simultaneous motion of from to , and of from to , while the current in changes from to , depends only on the initial state , , , and the final state , , , and not at all on the nature of the intermediate states through which the system may pass.
Hence the value of the total induction current must be of the formWith respect to the form of this function, we know, by Art. 536, that when there is no motion, and therefore and , the induction current is proportional to the primary current. Hence enters simply as a factor, the other factor being a function of the form and position of the circuits and .
We also know that the value of this function depends on the relative and not on the absolute positions of and , so that it must be capable of being expressed as a function of the distances of the different elements of which the circuits are composed, and of the angles which these elements make with each other.
Let be this function, then the total induction current may be writtenThese experiments, therefore, shew that the total current of induction depends on the change which takes place in a certain quantity, , and that this change may arise either from variation of the primary current , or from any motion of the primary or secondary circuit which alters .
540.] The conception of such a quantity, on the changes of which, and not on its absolute magnitude, the induction current depends, occurred to Faraday at an early stage of his researches[8]. He observed that the secondary circuit, when at rest in an electromagnetic field which remains of constant intensity, does not shew any electrical effect, whereas, if the same state of the field had been suddenly produced, there would have been a current. Again, if the primary circuit is removed from the field, or the magnetic forces abolished, there is a current of the opposite kind. He therefore recognised in the secondary circuit, when in the electromagnetic field, a 'peculiar electrical condition of matter,' to which he gave the name of the Electrotonic State. He afterwards found that he could dispense with this idea by means of considerations founded on the lines of magnetic force[9], but even in his latest researches[10], he says, 'Again and again the idea of an electrotonic state[11] has been forced upon my mind.'
The whole history of this idea in the mind of Faraday, as shewn in his published researches, is well worthy of study. By a course of experiments, guided by intense application of thought, but without the aid of mathematical calculations, he was led to recognise the existence of something which we now know to be a mathematical quantity, and which may even be called the fundamental quantity in the theory of electromagnetism. But as he was led up to this conception by a purely experimental path, he ascribed to it a physical existence, and supposed it to be a peculiar condition of matter, though he was ready to abandon this theory as soon as he could explain the phenomena by any more familiar forms of thought.
Other investigators were long afterwards led up to the same idea by a purely mathematical path, but, so far as I know, none of them recognised, in the refined mathematical idea of the potential of two circuits, Faraday's bold hypothesis of an electrotonic state. Those, therefore, who have approached this subject in the way pointed out by those eminent investigators who first reduced its laws to a mathematical form, have sometimes found it difficult to appreciate the scientific accuracy of the statements of laws which Faraday, in the first two series of his Researches, has given with such wonderful completeness.
The scientific value of Faraday's conception of an electrotonic state consists in its directing the mind to lay hold of a certain quantity, on the changes of which the actual phenomena depend. Without a much greater degree of development than Faraday gave it, this conception does not easily lend itself to the explanation of the phenomena. We shall return to this subject again in Art. 584.
541.] A method which, in Faraday's hands, was far more powerful is that in which he makes use of those lines of magnetic force which were always in his mind's eye when contemplating his magnets or electric currents, and the delineation of which by means of iron filings he rightly regarded[12] as a most valuable aid to the experimentalist.
Faraday looked on these lines as expressing, not only by their direction that of the magnetic force, but by their number and concentration the intensity of that force, and in his later researches[13] he shews how to conceive of unit lines of force. I have explained in various parts of this treatise the relation between the properties which Faraday recognised in the lines of force and the mathematical conditions of electric and magnetic forces, and how Faraday's notion of unit lines and of the number of lines within certain limits may be made mathematically precise. See Arts. 82, 404, 490.
In the first series of his Researches[14] he shews clearly how the direction of the current in a conducting circuit, part of which is moveable, depends on the mode in which the moving part cuts through the lines of magnetic force.
In the second series[15] he shews how the phenomena produced by variation of the strength of a current or a magnet may be explained, by supposing the system of lines of force to expand from or contract towards the wire or magnet as its power rises or falls.
I am not certain with what degree of clearness he then held the doctrine afterwards so distinctly laid down by him[16], that the moving conductor, as it cuts the lines of force, sums up the action due to an area or section of the lines of force. This, however, appears no new view of the case after the investigations of the second series[17] have been taken into account.
The conception which Faraday had of the continuity of the lines of force precludes the possibility of their suddenly starting into existence in a place where there were none before. If, therefore, the number of lines which pass through a conducting circuit is made to vary, it can only be by the circuit moving across the lines of force, or else by the lines of force moving across the circuit. In either case a current is generated in the circuit.
The number of the lines of force which at any instant pass through the circuit is mathematically equivalent to Faraday's earlier conception of the electrotonic state of that circuit, and it is represented by the quantity .
It is only since the definitions of electromotive force, Arts. 69, 274, and its measurement have been made more precise, that we can enunciate completely the true law of magneto-electric induction in the following terms:—
The total electromotive force acting round a circuit at any instant is measured by the rate of decrease of the number of lines of magnetic force which pass through it.
When integrated with respect to the time this statement becomes:—
The time-integral of the total electromotive force acting round any circuit, together with the number of lines of magnetic force which pass through the circuit, is a constant quantity.
Instead of speaking of the number of lines of magnetic force, we may speak of the magnetic induction through the circuit, or the surface-integral of magnetic induction extended over any surface bounded by the circuit.
We shall return again to this method of Faraday. In the mean time we must enumerate the theories of induction which are founded on other considerations.
Lenz's Law.
542.] In 1834, Lenz[18] enunciated the following remarkable relation between the phenomena of the mechanical action of electric currents, as defined by Ampère's formula, and the induction of electric currents by the relative motion of conductors. An earlier attempt at a statement of such a relation was given by Ritchie in the Philosophical Magazine for January of the same year, but the direction of the induced current was in every case stated wrongly. Lenz's law is as follows.—
If a constant current flows in the primary circuit ; and if, by the motion of , or of the secondary circuit , a current is induced in , the direction of this induced current will be such that, by its electromagnetic action on , it tends to oppose the relative motion of the circuits.
On this law J. Neumann[19] founded his mathematical theory of induction, in which he established the mathematical laws of the induced currents due to the motion of the primary or secondary conductor. He shewed that the quantity , which we have called the potential of the one circuit on the other, is the same as the electromagnetic potential of the one circuit on the other, which we have already investigated in connexion with Ampère's formula. We may regard J. Neumann, therefore, as having completed for the induction of currents the mathematical treatment which Ampère had applied to their mechanical action.
543.] A step of still greater scientific importance was soon after made by Helmholtz in his Essay on the Conservation of Force[20], and by Sir W. Thomson[21], working somewhat later, but independently of Helmholtz. They shewed that the induction of electric currents discovered by Faraday could be mathematically deduced from the electromagnetic actions discovered by Órsted and Ampère by the application of the principle of the Conservation of Energy.
Helmholtz takes the case of a conducting circuit of resistance , in which an electromotive force , arising from a voltaic or thermoelectric arrangement, acts. The current in the circuit at any instant is . He supposes that a magnet is in motion in the neighbourhood of the circuit, and that its potential with respect to the conductor is , so that, during any small interval of time , the energy communicated to the magnet by the electromagnetic action is .
The work done in generating heat in the circuit is, by Joule's law, Art. 242, , and the work spent by the electromotive force , in maintaining the current during the time , is . Hence, since the total work done must be equal to the work spent,In Helmholtz's original investigation he adopted a system of units founded on the measurement of the heat generated in the conductor by the current. Considering the unit of current as arbitrary, the unit of resistance is that of a conductor in which this unit current generates unit of heat in unit of time. The unit of electromotive force in this system is that required to produce the unit of current in the conductor of unit resistance. The adoption of this system of units necessitates the introduction into the equations of a quantity , which is the mechanical equivalent of the unit of heat. As we invariably adopt either the electrostatic or the electromagnetic system of units, this factor does not occur in the equations here given.
544.] Helmholtz also deduces the current of induction when a conducting circuit and a circuit carrying a constant current are made to move relatively to one another.
Let , be the resistances, , the currents, , the external electromotive forces, and the potential of the one circuit on the other due to unit current in each, then we have, as before,This shews that for equal currents the electromotive force of the first circuit on the second is equal to that of the second on the first, whatever be the forms of the circuits.
Helmholtz does not in this memoir discuss the case of induction due to the strengthening or weakening of the primary current, or the induction of a current on itself. Thomson[22] applied the same principle to the determination of the mechanical value of a current, and pointed out that when work is done by the mutual action of two constant currents, their mechanical value is increased by the same amount, so that the battery has to supply double that amount of work, in addition to that required to maintain the currents against the resistance of the circuits[23].
545.] The introduction, by W. Weber, of a system of absolute units for the measurement of electrical quantities is one of the most important steps in the progress of the science. Having already, in conjunction with Gauss, placed the measurement of magnetic quantities in the first rank of methods of precision, Weber proceeded in his Electrodynamic Measurements not only to lay down sound principles for fixing the units to be employed, but to make de terminations of particular electrical quantities in terms of these units, with a degree of accuracy previously unattempted. Both the electromagnetic and the electrostatic systems of units owe their development and practical application to these researches.
Weber has also formed a general theory of electric action from which he deduces both electrostatic and electromagnetic force, and also the induction of electric currents. We shall consider this theory, with some of its more recent developments, in a separate chapter. See Art. 846.
- ↑ Théorie des Phenomènes Electrodynamiques, p. 9.
- ↑ Exp. Res., ii. p. 293; iii. p. 447.
- ↑ Read Faraday's Experimental Researches, series i and ii.
- ↑ Pogg., Ann. xxi. 483 (1834.)
- ↑ Exp. Res., 195.
- ↑ Ib., 200.
- ↑ Annales de Chimie, xxxiv. p. 66 (1852), and Nuovo Cimento, ix. p. 345 (1859).
- ↑ Exp. Res., series i. 60.
- ↑ Ib., series ii. (242).
- ↑ Ib., 3269.
- ↑ Ib., 60, 1114, 1661, 1729, 1733.
- ↑ Exp. Res., 3234.
- ↑ Ib., 3122.
- ↑ Ib., 114.
- ↑ Exp. Res., 238.
- ↑ Ib., 3082, 3087, 3113.
- ↑ Ib., 217. &c.
- ↑ Pogg., Ann. xxxi. 483 (1834).
- ↑ Berlin Acad., 1845 and 1847.
- ↑ Read before the Physical Society of Berlin, July 23, 1847. Translated in Taylor's 'Scientific Memoirs,' part ii. p. 114.
- ↑ Trans. Brit. Ass., 1848, and Phil. Mag., Dec. 1851. See also his paper on Transient Electric Currents, Phil. Mag., 1853.
- ↑ Mechanical Theory of Electrolysis, Phil. Mag., Dec., 1851.
- ↑ Nichol's Cyclopaedia of Physical Science, ed. 1860, Article 'Magnetism, Dynamical Relations of,' and Reprint, § 571
























































