represents one million of such units in nature. The second method is still employed in many cases, and we find thus:—
| 1 | in. | = | 1 | statute mile (of 63,366 in.) | corresponds to | 1 | : | 63,366 | ||||
| 6 | in. | = | 1 | ,, | ,, | ,, | ,, | 1 | : | 10,560 | ||
| 1 | in. | = | 5 chains (of 858 in.) | . | . | ,, | 1 | : | 4,890 | |||
| 1 | in. | = | 1 nautical mile (of 73,037 in.) | . | ,, | 1 | : | 73,037 | ||||
| 1 | in. | = | 1 verst (of 42,000 in.) | . | . | ,, | 1 | : | 42,000 | |||
| 2 Vienna in. = 1 Austrian mile (of 288,000 in.) | ,, | 1 | : | 144,000 | ||||||||
| 1 | cm. | = | 500 metres (of 100 cm.) | . | . | ,, | 1 | : | 50,000 | |||
In cases where the draughtsman has omitted to indicate the scale we can ascertain it by dividing the actual length of a meridian degree by the length of a degree measure upon the map. Thus a degree between 50° and 51° measures 111,226,000 mm.; on the map it is represented by 111 mm. Hence the scale is 1:1,000,000 approximately.
The linear scale of maps can obviously be used only in the case of maps covering a small area, for in the case of maps of greater extension measurements would be vitiated owing to the distortion or exaggeration inherent in all projections, not to mention the expansion or shrinking of the paper in the process of printing. As an extreme instance of the misleading character of the scale given on maps embracing a wide area we may refer to a map of a hemisphere. The scale of that map, as determined by the equator or centre meridian, we will suppose to be 1:125,000,000, while the encircling meridian indicates a scale of 1:80,000,000; and a “mean” scale, equal to the square root of the proportion which the area of the map bears to the actual area of a hemisphere, is 1:112,000,000. In adopting a scale for their maps, cartographers will do well to choose a multiple of 1000 if possible, for such a scale can claim to be international, while in planning an atlas they ought to avoid a needless multiplicity of scales.
Map Projections are dealt with separately below. It will suffice therefore to point out that the ordinary needs of the cartographer can be met by conical projections, and, in the case of maps covering a wide area, by Lambert’s equal area projection. The indiscriminate use of Mercator’s projection, for maps of the world, is to be deprecated owing to the inordinate exaggeration of areas in high latitudes. In the case of topographical maps sheets bounded by meridians and parallels are to be commended.
The meridian of Greenwich has been universally accepted as the initial meridian, but in the case of most topographical maps of foreign countries local meridians are still adhered to—the more important among which are:—
| Paris (Obs. nationale) | . | . | 2° 20′ 14″ E. | of Greenwich. | ||
| Pulkova (St Petersburg) | . | 30° 19′ 39″ E. | ,, | |||
| Stockholm | . | . | . | . | 18°3′ 30″ E. | ,, |
| Rome (Collegio Romano) | . | 12° 28′ 40″ E. | ,, | |||
| Brussels (Old town) | . | . | 4° 22′ 11″ E. | ,, | ||
| Madrid . | . | . | . | . | 3° 41′ 16″ W. | ,, |
| Ferro (assumed) | . | . | . | 20°0′0″ W. | of Paris. | |
The outline includes coast-line, rivers, roads, towns, and in fact all objects capable of being shown on a map, with the exception of the hills and of woods, swamps, deserts and the like, which the draughtsman generally describes as “ornament.” Conventional signs and symbols are universally used in depicting these objects.
Delineation of the Ground.—The mole-hills and serrated ridges of medieval maps were still in almost general use at the close of the 18th century, and are occasionally met with at the present day, being cheaply produced, readily understood by the unlearned, and in reality preferable to the uncouth and misleading hatchings still to be seen on many maps. Far superior are those scenographic representations which enable a person consulting the map to identify prominent landmarks, such as the Pic du Midi, which rises like a pillar to the south of Pau, but is not readily discovered upon an ordinary map. This advantage is still fully recognized, for such views of distant hills are still commonly given on the margin of marine charts for the assistance of navigators; military surveyors are encouraged to introduce sketches of prominent landmarks upon their reconnaissance plans, and the general public is enabled to consult “Picturesque Relief Maps”—such as F. W. Delkeskamp’s Switzerland (1830) or his Panorama of the Rhine. Delineations such as these do not, however, satisfy scientific requirements. All objects on a map are required to be shown as projected horizontally upon a plane. This principle must naturally be adhered to when delineating the features of the ground. This was recognized by J. Picard and other members of the Academy of Science whom Colbert, in 1668, directed to prepare a new map of France, for on David Vivier’s map of the environs of Paris (1674, scale 1:86,400) very crude hachures bounding the rivers have been substituted for the scenographic hills of older maps.
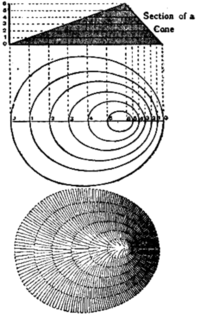
Little progress in the delineation of the ground, however, was made until towards the close of the 18th century, when horizontal contours and hachures regulated according to the angle of inclination of all slopes, were adopted. These contours intersect the ground at a given distance above or below the level of the sea, and thus bound a series of horizontal planes (see fig. 1). Contours of this kind were first utilized by M. S. Cruquius in his chart of the Merwede (1728); Philip Buache (1737) introduced such contours or isobaths (Gr. ἶσος, equal; βαθύς, deep) upon his chart of the Channel, and intended to introduce similar contours or isohypses (ὕψος, height) for a representation of the land. Dupain-Triel, acting upon a suggestion of his friend M. Ducarla, published his La France considérée dans les différentes hauteurs de ses plaines (1791), upon which equidistant contours at intervals of 16 toises found a place. The scientific value of these contoured maps is fully recognized. They not only indicate the height of the land, but also enable us to compute the declivity of the mountain slopes; and if minor features of ground lying between two contours—such as ravines, as also rocky precipices and glaciers—are indicated, as is done on the Siegfried atlas of Switzerland, they fully meet the requirements of the scientific man, the engineer and the mountain-climber. At the same time it cannot be denied that these maps, unless the contours are inserted at short intervals, lack graphic expression. Two methods are employed to attain this: the first distinguishes the strata or layers by colours; the second indicates the varying slopes by shades or hachures. The first of these methods yields a hypsographical, or—if the sea-bottom be included, in which case all contours are referred to a common datum line—a bathy hypsographical map. Carl Ritter, in 1806, employed graduated tints, increasing in lightness on proceeding from the lowlands to the highlands; while General F. von Hauslab, director of the Austrian Surveys, in 1842, advised that the darkest tints should be allotted to the highlands, so that they might not obscure details in the densely peopled plains. The desired effect may be produced by a graduation of the same colour, or by a polychromatic scale—such as white, pale red, pale brown, various shades of green, violet and purple, in ascending order. C. von Sonklar, in his map of the Hohe Tauern (1:144,000; 1864) coloured plains and valleys green; mountain slopes in five shades of brown; glaciers blue or white. E. G. Ravenstein’s map of Ben Nevis (1887) first employed the colours of the spectrum, viz. green to brown, in ascending order for the land; blue, indigo and violet for the sea, increasing in intensity with the height or the depth. At first cartographers chose their colours rather arbitrarily. Thus Horsell, who was the first to introduce tints