the ellipse is to be drawn. When pm is greater than pa the ellipse touches the circle in two points; these points divide the ellipse into two parts, one of which, being on the other side of the meridian plane aqr, is invisible. Fig. 6 shows the complete orthographic projection.
 |
| Fig. 7. |
 |
| Fig. 8. |
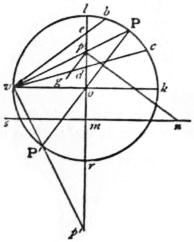
Stereographic Projection.—In this case the point of vision is on the surface, and the projection is made on the plane of the great circle whose pole is V. Let kpl V (fig. 7) be a great circle through the point of vision, and ors the trace of the plane of projection. Let c be the centre of a small circle whose radius is cp = cl; the straight line pl represents this small circle in orthographic projection.
We have first to show that the stereographic projection of the small circle pl is itself a circle; that is to say, a straight line through V, moving along the circumference of pl, traces a circle on the plane of projection ors. This line generates an oblique cone standing on a circular base, its axis being cV (since the angle pVc = angle cVl); this cone is divided symmetrically by the plane of the great circle kpl, and also by the plane which passes through the axis Vc, perpendicular to the plane kpl. Now Vr·Vp, being = Vo sec kVp·Vk cos kVp = Vo·Vk, is equal to Vs·Vl; therefore the triangles Vrs, Vlp are similar, and it follows that the section of the cone by the plane rs is similar to the section by the plane pl. But the latter is a circle, hence also the projection is a circle; and since the representation of every infinitely small circle on the surface is itself a circle, it follows that in this projection the representation of small parts is strictly similar. Another inference is that the angle in which two lines on the sphere intersect is represented by the same angle in the projection. This may otherwise be proved by means of fig. 8, where Vok is the diameter of the sphere passing through the point of vision, fgh the plane of projection, kt a great circle, passing of course through V, and ouv the line of intersection of these two planes. A tangent plane to the surface at t cuts the plane of projection in the line rvs perpendicular to ov; tv is a tangent to the circle kt at t, tr and ts are any two tangents to the surface at t. Now the angle vtu (u being the projection of t) is 90° − otV = 90° − oVt = ouV = tuv, therefore tv is equal to uv; and since tvs and uvs are right angles, it follows that the angles vts and vus are equal. Hence the angle rts also is equal to its projection rus; that is, any angle formed by two intersecting lines on the surface is truly represented in the stereographic projection.
In this projection, therefore, angles are correctly represented and every small triangle is represented by a similar triangle. Projections having this property of similar representation of small parts are called orthomorphic, conform or conformable. The word orthomorphic, which was introduced by Germain[1] and adopted by Craig,[2] is perhaps the best to use.
Since in orthomorphic projections very small figures are correctly represented, it follows that the scale is the same in all directions round a point in its immediate neighbourhood, and orthomorphic projections may be defined as possessing this property. There are many other orthomorphic projections, of which the best known is Mercator’s. These are described below.
We have seen that the stereographic projection of any circle of the sphere is itself a circle. But in the case in which the circle to be projected passes through V, the projection becomes, for a great circle, a line through the centre of the sphere; otherwise, a line anywhere. It follows that meridians and parallels are represented in a projection on the horizon of any place by two systems of orthogonally cutting circles, one system passing through two fixed points, namely, the poles; and the projected meridians as they pass through the poles show the proper differences of longitude.
 |
| Fig. 9. |
 |
| Fig. 10. |
To construct a stereographic projection of the sphere on the horizon of a given place. Draw the circle vlkr (fig. 9) with the diameters kv, lr at right angles; the latter is to represent the central meridian. Take koP equal to the co-latitude of the given place, say u; draw the diameter PoP′, and vP, vP′ cutting lr in pp′: these are the projections of the poles, through which all the circles representing meridians have to pass. All their centres then will be in a line smn which crosses pp′ at right angles through its middle point m. Now to describe the meridian whose west longitude is ω, draw pn making the angle opn = 90° − ω, then n is the centre of the required circle, whose direction as it passes through p will make an angle opg = ω with pp′. The lengths of the several lines are
Again, for the parallels, take Pb = Pc equal to the co-latitude, say c, of the parallel to be projected; join vb, vc cutting lr in e, d. Then ed is the diameter of the circle which is the required projection; its centre is of course the middle point of ed, and the lengths of the lines are
The line sn itself is the projection of a parallel, namely, that of which the co-latitude c = 180° − u, a parallel which passes through the point of vision.
Notwithstanding the facility of construction, the stereographic projection is not much used in map-making. It is sometimes used for maps of the hemispheres in atlases, and for star charts.
External Perspective Projection.—We now come to the general case in which the point of vision has any position outside the sphere. Let abcd (fig. 10) be the great circle section of the sphere by a plane passing through c, the central point of the portion of surface to be represented, and V the point of vision. Let pj perpendicular to Vc be the plane of representation, join mV cutting pj in f, then f is the projection of any point m in the circle abc, and ef is the representation of cm.
Let the angle com = u, Ve = k, Vo = h, ef = ρ; then, since ef: eV = mg : gV, we have ρ = k sin u/(h + cos u), which gives the law connecting a spherical distance u with its rectilinear representation ρ. The relative scale at any point in this system of projection is given by
| σ = dρ / du, σ′ = ρ / sin u, |
| σ = k (1 + h cos u) / (h + cos u)2; σ′ = k / (h + cos u), |
the former applying to measurements made in a direction which passes through the centre of the map, the latter to the transverse direction. The product σσ′ gives the exaggeration of areas. With respect to the alteration of angles we have Σ = (h + cos u) / (l + k cos u), and the greatest alteration of angle is
| sin−1 ( | h − 1 | tan2 | u | ). |
| h + 1 | 2 |
This vanishes when h = 1, that is if the projection be stereographic; or for u = 0, that is at the centre of the map. At a distance of 90° from the centre, the greatest alteration is 90° − 2 cot−1 √h. (See Phil. Mag. 1862.)
Clarke’s Projection.—The constants h and k can be determined, so that the total misrepresentation, viz.:
shall be a minimum, β being the greatest value of u, or the spherical radius of the map. On substituting the expressions for σ and σ′ the integration is effected without difficulty. Put
| λ = (1 − cos β) / (h + cos β); ν = (h − 1) λ, |
| H = ν − (h + 1) loge (λ + 1), H′ = λ (2 − ν + 13ν2) / (h + 1). |
Then the value of M is
When this is a minimum,
∴ kH′ + H = 0; 2 dH / dh + kdhH′ / dh = 0.
Therefore M = 4 sin2 12β − H2/H1, and h must be determined so as to make H2 : H′ a maximum. In any particular case this maximum can only be ascertained by trial, that is to say, log H2 − log H′ must be calculated for certain equidistant values of h, and then the

