The Elements of Euclid for the Use of Schools and Colleges/Book I.

by Isaac Todhunter

 

EUCLID'S ELEMENTS.

BOOK I.

DEFINITIONS.

1. A point is that which has no parts, or which has no magnitude.

2. A line is length without breadth.

3. The extremities of a line are points.

4. A straight line is that which lies evenly between its extreme points.

5. A superficies is that which has only length and breadth.

6. The extremities of a superficies are lines.

7. A plane superficies is that in which any two points being taken, the straight line between them lies wholly in that superficies.

8. A plane angle is the inclination of two lines to one another in a plane, which meet together, but are not in the same direction.

9. A plane rectilineal angle is the inclination of two straight lines to one another, which meet together, but are not in the same straight line.

Note. When several angles are at one point B, any one of them is expressed by three letters, of which the letter which is at the vertex of the angle, that is, at the point at which the straight lines that contain the angle meet one another, is put between the other two letters, and one of these two letters is somewhere on one of those straight lines, and the other letter on the other straight line. Thus, the angle which is contained by the

straight lines AB, CB is named the angle ABC, or CBA; the angle which is contained by the straight lines AB, DB is named the angle ABD, or DBA; and the angle which is contained by the straight lines DB, CB is named the angle DBC, or CBD; but if there be only one angle at a point, it may be expressed by a letter placed at that point; as the angle at E.

10. When a straight line standing on another straight line, makes the adjacent angles equal to one another, each of the angles is called a right angle; and the straight line which stands on the other is called a perpendicular to it.

11. An obtuse angle is that which is greater than a right angle.

12. An acute angle is that which is less than a right angle.

13. A term or boundary is the extremity of any thing.

14. A figure is that which is enclosed by one or more boundaries.

15. A circle is a plane figure contained by one line, which is called the circumference, and is such, that all straight lines drawn from a certain point within the figure to the circumference are equal to one another:

16. And this point is called the centre of the circle.

17. A diameter of a circle is a straight line drawn through the centre, and terminated both ways by the circumference.

[A radius of a circle is a straight line drawn from the centre to the circumference.]

18. A semicircle is the figure contained by a diameter and the part of the circumference cut off by the diameter.

19. A segment of a circle is the figure contained by a straight line and the circumference which it cuts off.

20. Rectilineal figures are those which are contained by straight lines:

21. Trilateral figures, or triangles, by three straight lines:

22. Quadrilateral figures by four straight lines:

23. Multilateral figures, or polygons, by more than four straight lines.

24. Of three-sided figures,

An equilateral triangle is that which has three equal sides:

25. An isosceles triangle is that which has two sides equal:

26. A scalene triangle is that which has three unequal sides:

27. A right-angled triangle is that which has a right angle:

[The side opposite to the right angle in a right-angled triangle is frequently called the hypotenuse.]

28. An obtuse-angled triangle is that which has an obtuse angle:

29. An acute-angled triangle is that which has three acute angles.

Of four-sided figures,

30. A square is that which has all its sides equal, and all its angles right angles:

31. An oblong is that which has all its angles right angles, but not all its sides equal:

32. A rhombus is that which has all its sides equal, but its angles are not right angles:

33. A rhomboid is that which has its opposite sides equal to one another, but all its sides are not equal, nor its angles right angles:

34. All other four-sided figures besides these are called trapeziums.

35. Parallel straight lines are such as are in the same plane, and which being produced ever so far both ways do not meet.

[Note. The terms oblong and rhomboid are not often used. Practically the following definitions are used. Any four-sided figure is called a quadrilateral. A line joining two opposite angles of a quadrilateral is called a diagonal. A quadrilateral which has its opposite sides parallel is called a parallelogram'. The words square and rhombus are used in the sense defined by Euclid; and the word rectangle is used instead of the word oblong.

Some writers propose to restrict the word trapezium to a quadrilateral which has two of its sides parallel; and it would certainly be convenient if this restriction were universally adopted.]

 

POSTULATES.

Let it be granted,

1. That a straight line may be drawn from any one point to any other point:

2. That a terminated straight line may be produced to any length in a straight line:

3. And that a circle may be described from any centre, at any distance from that centre.

AXIOMS.

1. Things which are equal to the same thing are equal to one another.

2. If equals be added to equals the wholes are equal.

3. If equals be taken from equals the remainders are equal.

4. If equals be added to unequals the wholes are unequal.

5. If equals be taken from unequals the remainders are unequal.

6. Things which are double of the same thing are equal to one another.

7. Things which are halves of the same thing are equal to one another.

8. Magnitudes which coincide with one another, that is, which exactly fill the same space, are equal to one another.

9. The whole is greater than its part.

10. Two straight lines cannot enclose a space.

11. All right angles are equal to one another.

12. If a straight line meet two straight lines, so as to make the two interior angles on the same side of it taken together less than two right angles, these straight lines, being continually produced, shall at length meet on that side on which are the angles which are less than two right angles.

PROPOSITION 1. PROBLEM.

To describe an equilateral triangle on a given finite straight line.

Let AB be the given straight line; it is required to describe an equilateral triangle on AB.

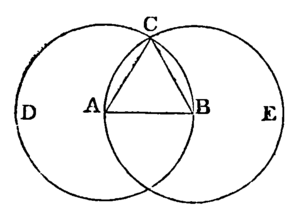
From the centre A at the distance AB describe the circle BCD. [Postulate 3.

From the centre B, at the distance BA, describe the circle ACE. [Postulate 3.

From the point C, at which the circles cut one another, draw the straight lines CA and CB to the points A and B. [Post. 1.

ABC shall be an equilateral triangle.

Because the point A is the centre of the circle BCD, AC is equal to AB. [Definition 15.

And because the point B is the centre of the circle ACE, BC is equal to BA. [Definition 15.

But it has been shewn that CA is equal to AB;

therefore CA and CB are each of them equal to AB.

But things which are equal to the same thing are equal to one another. [Axiom 1.

Therefore CA is equal to CB.

Therefore CA, AB, BC are equal to one another.

Wherefore the triangle ABC is equilateral, [Def. 24. and it is described on the given straight line AB. Q.E.F.

PROPOSITION 2. PROBLEM.

From a given point to draw a straight line equal to a given straight line.

Let A be the given point, and BC the given straight line: it is required to draw from the point A a straight line equal to BC.

From the point A to B draw the straight line AB; [Post. 1.
and on it describe the equilateral triangle DAB, [I. 1.
and produce the straight lines DA, DB to E and F. [Post. 2.
From the centre B, at the distance BC, describe the circle CGH, meeting DF at G. [Post. 3.
From the centre D, at the distance DG, describe the circle GKL, meeting DE at L. [Post. 3.
AL shall be equal to BC.

Because the point B is the centre of the circle CGH, BC is equal to BG. [Definition 15.
And because the point D is the centre of the circle GKL, DL is equal to DG; [Definition 15.
and DA, DB parts of them are equal; [Definition 24.
therefore the remainder AL is equal to the remainder BG. [Axiom 3.
But it has been shewn that BC is equal to BG;
therefore AL and BC are each of them equal to BG.
But things which are equal to the same thing are equal to one another. [Axiom 1.
Therefore AL is equal to BC.

Wherefore from the given point A a straight line AL has been drawn equal to the given straight line BC. q.e.f.

PROPOSITION 3. PROBLEM.

From the greater of two given straight lines to cut off a part equal to the less.

Let AB and C be the two given straight lines, of which AB is the greater: it is required to cut off from AB the greater, a part equal to C the less.

From the point A draw the straight line AD equal to C; [I. 2.
and from the centre A, at the distance AD, describe the circle DEF meeting AB at E. [Postulate 3.
AE shall be equal to C.

Because the point A is the centre of the circle DEF, AE is equal to AD. [Definition 15.
But C is equal to AD. [Construction.
Therefore AE and C are each of them equal to AD.
Therefore AE is equal to C. [Axiom 1.

Wherefore from AB the greater of two given straight lines a part AE has been cut off equal to C the less. q.e.f.

PROPOSITION 4. THEOREM.

If two triangles have two sides of the one equal to two sides of the other, each to each, and have also the angles contained by those sides equal to one another, they shall also have their bases or third sides equal; and the two triangles shall be equal, and their other angles shall be equal, each to each, namely those to which the equal sides are opposite.

Let ABC, DEF be two triangles which have the two sides AB, AC equal to the two sides DE, DF, each to each, namely, AB to DE, and AC to DF, and the angle BAC equal to the angle EDF: the base BC shall be equal to the base EF, and the triangle ABC to the triangle DEF, and the other angles shall be equal, each to each, to which the equal sides are opposite, namely, the angle ABC to the angle DEF, and the angle ACB to the angle DFE.

For if the triangle ABC be applied to the triangle DEF, so that the point A may be on the point D, and the straight line AB on the straight line DE, the point B will coincide with the point E, because AB is equal to DE, [Hyp.

And, AB coinciding with DE, AC will fall on DF, because the angle BAC is equal to the angle EDF. [Hypothesis.

Therefore also the point C will coincide with the point F, because AC is equal to DF. [Hypothesis.

But the point B was shewn to coincide with the point E, therefore the base BC will coincide with the base EF;

because, B coinciding with E and C with F, if the base BC does not coincide with the base EF, two straight lines will enclose a space; which is impossible. [Axiom 10.

Therefore the base BC coincides with the base EF, and is equal to it. [Axiom 8.

Therefore the whole triangle ABC coincides with the whole triangle DEF, and is equal to it. [Axiom 8.

And the other angles of the one coincide with the other angles of the other, and are equal to them, namely, the angle ABC to the angle DEF, and the angle ACB to the angle DFE.

Wherefore, if two triangles &c. q.e.d.

PROPOSITION 5. THEOREM.

The angles at the base of an isosceles triangle are equal to one another; and if the equal sides be produced the angles on the other side of the base shall be equal to one another.

Let ABC be an isosceles triangle, having the side AB equal to the side AC, and let the straight lines AB, AC be produced to D and E: the angle ABC shall be equal to the angle ACB, and the angle CBD to the angle BCE.

In BD take any point F,

and from AE the greater cut off AG equal to AF the less, [I.3.

and join FC, GB.

Because AF is equal to AG [Constr.

and AB to AC, [Hypothesis.

the two sides FA, AC are equal to the two sides GA, AB, each to each; and they contain the angle FAG common to the two triangles AFC, AGB;

therefore the base FC is equal to the base GB, and the triangle AFC to the triangle AGB, and the remaining angles of the one to the remaining angles of the other, each to each, to which the equal sides are opposite, namely the angle ACF to the angle ABG, and the angle AFC to the angle AGB. [I. 4.

And because the whole AF is equal to the whole AG, of which the parts AB, AC are equal, [Hypothesis.

the remainder BF is equal to the remainder CG. [Axiom 3.

And FC was shewn to be equal to GB;

therefore the two sides BF, FC are equal to the two sides CG, GB, each to each;

and the angle BFC was shewn to be equal to the angle CGB; therefore the triangles BFC, CGB are equal, and their other angles are equal, each to each, to which the equal sides are opposite, namely the angle FBC to the angle GCB, and the angle BCF to the angle CBG. [I. 4.

And since it has been shewn that the whole angle ABG is equal to the whole angle ACF,

and that the parts of these, the angles CBG, BCF are also equal;

therefore the remaining angle ABC is equal to the remaining angle ACB, which are the angles at the base of the triangle ABC. [Axiom 3.

And it has also been shewn that the angle FBC is equal to the angle GCB, which are the angles on the other side of the base.

Wherefore, the angles &c. q.e.d.

Corollary. Hence every equilateral triangle is also equiangular.

PROPOSITION 6. THEOREM.

If two angles of a triangle be equal to one another, the sides also which subtend, or are opposite to, the equal angles, shall be equal to one another.

Let ABC be a triangle, having the angle ABC equal to the angle ACB: the side AC shall be equal to the side AB.

For if AC be not equal to AB, one of them must be greater than the other.

Let AB be the greater, and from it cut off DB equal to AC the less, [I. 3.

and join DC.

Then, because in the triangles DBC, ACB, DB is equal to AC, [Construction.

and BC is common to both,

the two sides DB, BC are equal to the two sides AC, CB each to each;

and the angle DBC is equal to the angle ACB; [Hypothesis.

therefore the base DC is equal to the base AB, and the triangle DBC is equal to the triangle ACB, [I. 4.

the less to the greater; which is absurd. [Axiom 9.

Therefore AB is not unequal to AC, that is, it is equal to it.

Wherefore, if two angles &c. q.e.d.

Corollary. Hence every equiangular triangle is also equilateral.

PROPOSITION 7. THEOREM.

On the same base, and on the same side of it, there cannot be two triangles having their sides which are terminated at one extremity of the base equal to one another, and likewise those which are terminated at the other extremity equal to one another.

If it be possible, on the same base AB, and on the same side of it, let there be two triangles ACB, ADB, having their sides CA, DA, which are terminated at the extremity A of the base, equal

to one another, and likewise their sides CB, DB, which are terminated at B equal to one another.

Join CD. In the case in which the vertex of each triangle is without the other triangle;

because AC is equal to AD,[Hypothesis.

the angle ACD is equal to the angle ADC.[I. 5.

But the angle ACD is greater than the angle BCD,[Ax. 9.

therefore the angle ADC is also greater than the angle BCD;

much more then is the angle BDC greater than the angle BCD.

Again, because BC is equal to BD,[Hypothesis.

the angle BDC is equal to the angle BCD.[I. 5.

But it has been shewn to be greater; which is impossible.

float

But if one of the vertices as D, be within the other triangle ACB, produce AC, AD to E, F.

Then because AC is equal to AD, in the triangle ACD, [Hyp.

the angles ECD, FDC, on the other side of the base CD, are equal to one another. [I. 5.

But the angle ECD is greater than the angle BCD, [Axiom 9.

therefore the angle FDC is also greater than the angle BCD;

much more then is the angle BDC greater than the angle BCD.

Again, because BC is equal to BD, [Hypothesis.

the angle BDC is equal to the angle BCD. [I. 5.

But it has been shewn to be greater; which is impossible.

The case in which the vertex of one triangle is on a side of the other needs no demonstration.

Wherefore, on the same base &c. q.e.d.

PROPOSITION 8. THEOREM.

If two triangles have two sides of the one equal to two sides of the other, each to each, and have likewise their bases equal, the angle which is contained by the two sides of the one shall be equal to the angle which is contained by the two sides, equal to them, of the other.

Let ABC, DEF be two triangles, having the two sides AB, AC equal to the two sides DE, DF, each to each, namely AB to DE, and AC to DF, and also the base BC equal to the base EF: the angle BAC shall be equal to the angle EDF.

For if the triangle ABC be applied to the triangle DEF, so that the point B may be on the point E, and the straight line BC on the straight line EF, the point C will also coincide with the point F, because BC is equal to EF. [Hyp.

Therefore, BC coinciding with EF, BA and AC will coincide with ED and DF.

For if the base BC coincides with the base EF, but the sides BA, CA do not coincide with the sides ED, FD, but have a different situation as EG, FG; then on the same base and on the same side of it there will be two triangles having their sides which are terminated at one extremity of the base equal to one another, and likewise their sides which are terminated at the other extremity.

But this is impossible. [I. 7.

Therefore since the base BC coincides with the base EF, the sides BA, AC must coincide with the sides ED, DF. Therefore also the angle BAC coincides with the angle EDF, and is equal to it. [Axiom 8.

Wherefore, if two triangles &c. q.e.d.

PROPOSITION 9. PROBLEM.

To bisect a given rectilineal angle, that is to divide it into two equal angles.

float

Let BAC be the given rectilineal angle: it is required to bisect it.

Take any point D in AB, and from AC cut off AE equal to AD; [I. 3.

join DE, and on DE, on the side remote from A, describe the equilateral triangle DEF. [I. 1.

Join AF. The straight line AF shall bisect the angle BAC.

Because AD is equal to AE, [Construction.

and AF is common to the two triangles DAF, EAF,

the two sides DA, AF are equal to the two sides EA, AF, each to each;

and the base DF is equal to the base EF; [Definition 24.

therefore the angle DAF is equal to the angle EAF. [I. 8.

Wherefore the given rectilineal angle BAC is bisected by the straight line AF. q.e.f.

PROPOSITION 10. PROBLEM.

To bisect a given finite straight line, that is to divide it into two equal parts.

float

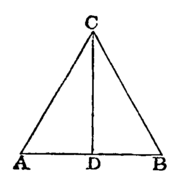
Let AB be the given straight line; it is required to divide it into two equal parts.

Describe on it an equilateral triangle ABC, [I. 1.

and bisect the angle ACB by the straight line CD, meeting AB at D. [I. 9.

AB shall be cut into two equal parts at the point D.

Because AC is equal to CB, [Definition 24.

and CD is common to the two triangles ACD, BCD,

the two sides AC, CD are equal to the two sides BC, CD, each to each;

and the angle ACD is equal to the angle BCD; [Constr.

therefore the base AD is equal to the base DB. [I. 4.

Wherefore the given straight line AB is divided into two equal parts at the point D. q.e.f.

PROPOSITION 11. PROBLEM.

To draw a straight line at right angles to a given straight line, from a given point in the same.

float

Let AB be the given straight line, and C the given point in it: it is required to draw from the point C a straight line at right angles to AB.

Take any point D in AC and make CE equal to CD [I. 3

On DE describe the equilateral triangle DFE, [I. 1

and join CF.

The straight line CF drawn from the given point C shall be at right angles to the given straight line AB.

Because DC is equal to CE, [Construction.

and CF is common to the two triangles DCF, ECF;

the two sides DC, CF are equal to the two sides EC, CF, each to each;

and the base DF is equal to the base EF; [Definition 24.

therefore the angle DCF is equal to the angle ECF; [I. 8.

and they are adjacent angles.

But when a straight line, standing on another straight line, makes the adjacent angles equal to one another, each of the angles is called a right angle; [Definition 10.

therefore each of the angles DCF, ECF is a right angle.

Wherefore from the given point C in the given straight line AB, CF has been drawn at right angles to AB. q.e.f.

Corollary. By the help of this problem it may be shewn that two straight lines cannot have a common segment.

float

If it be possible, let the two straight lines ABC, ABD have the segment AB common to both of them.

From the point B draw BE at right angles to AB.

Then, because ABC is a straight line, [Hypothesis.

the angle CBE is equal to the angle EBA. [Definition 10.

Also, because ABD is a straight line, [Hypothesis.

the angle DBE is equal to the angle EBA.

Therefore the angle DBE is equal to the angle CBE, [Ax. 1.

the less to the greater; which is impossible. [Axiom 9.

Wherefore two straight lines cannot have a common segment.

PROPOSITION 12. PROBLEM.

To draw a straight line perpendicular to a given straight line of an unlimited length, from a given point without it.

Let AB be the given straight line, which may be produced to any length both ways, and let C be the given point without it: it is required to draw from the point C a straight line perpendicular to AB.

float

Take any point D on the other side of AB, and from the centre C, at the distance CD, describe the circle EGF, meeting AB at F and G. [Postulate 3.

Bisect FG at H, [I. 10.

and join CH.

The straight line CH drawn from the given point C shall be perpendicular to the given straight line AB.

Join CF, CG.

Because FH is equal to HG, [Construction.

and HC is common to the two triangles FHC, GHC;

the two sides FH,HC are equal to the two sides GH, HC, each to each;

and the base CF is equal to the base CG; [Definition 15.

therefore the angle CHF is equal to the angle CHG; [I. 8.

and they are adjacent angles.

But when a straight line, standing on another straight line, makes the adjacent angles equal to one another, each of the angles is called a right angle, and the straight line which stands on the other is called a perpendicular to it. [Def. 10.

Wherefore a perpendicular CH has been drawn to the given straight line AB from the given point C without it. q.e.f.

PROPOSITION 13. THEOREM.

The angles which one straight line makes with another straight line on one side of it, either are two right angles, or are together equal to two right angles.

Let the straight line AB make with the straight line CD, on one side of it, the angles CBA, ABD: these either are two right angles, or are together equal to two right angles.

For if the angle CBA is equal to the angle ABD, each of them is a right angle. [Definition 10.

But if not, from the point B draw BE at right angles to CD; [I. 11.

therefore the angles CBE, EBD are two right angles, [Def. 10.

Now the angle CBE is equal to the two angles CBA, ABE; to each of these equals add the angle EBD;

therefore the angles CBE, EBD are equal to the three angles CBA, ABE, EBD. [Axiom 2.

Again, the angle DBA is equal to the two angles DBE, EBA;

to each of these equals add the angle ABC;

therefore the angles DBA, ABC are equal to the three angles DBE, EBA, ABC. [Axiom 2.

But the angles CBE, EBD have been shewn to be equal to the same three angles.

Therefore the angles CBE, EBD are equal to the angles DBA, ABC [Axiom 1.

But CBE, EBD are two right angles;

therefore DBA, ABC are together equal to two right angles.

Wherefore, the angles &c. q.e.d.

PROPOSITION 14. THEOREM.

If, at a point in a straight line, two other straight lines, on the opposite sides of it, make the adjacent angles together equal to two right angles, these two straight lines shall be in one and the same straight line.

At the point B in the straight line AB, let the two straight lines BC, BD, on the opposite sides of AB, make the adjacent angles ABC, ABD together equal to two right angles: BD shall be in the same straight line with CB.

float

For if BD be not in a the same straight line with CB, let BE be in the same straight line with it.

Then because the straight line AB makes with the straight line CBE, on one side of it, the angles ABC, ABE, these angles are together equal to two right angles. [I. 13.

But the angles ABC, ABD are also together equal to two right angles. [Hypothesis.

Therefore the angles ABC, ABE are equal to the angles ABC, ABD.

From each of these equals take away the common angle ABC, and the remaining angle ABE is equal to the remaining angle ABD, [Axiom 3.

the less to the greater; which is impossible.

Therefore BE is not in the same straight line with CB.

And in the same manner it may be shewn that no other can be in the same straight line with it but BD;

therefore BD is in the same straight line with CB.

Wherefore, if at a point &c. q.e.d.

PROPOSITION 15. THEOREM.

If two straight lines cut one another, the vertical, or opposite, angles shall be equal.

float

Let the two straight lines AB, CD cut one another at the point E; the angle AEC shall be equal to the angle DEB, and the angle CEB to the angle AED.

Because the straight line AE makes with the straight line CD the angles CEA, AED, those angles are together equal to two right angles. [I. 13.

Again, because the straight line DE makes with the straight line AB the angles AED, DEB, these also are together equal to two right angles. [I. 13.

But the angles CEA, AED have been shewn to be together equal to two right angles.

Therefore the angles CEA,AED are equal to the angles AED, DEB.

From each of these equals take away the common angle AED, and the remaining angle CEA is equal to the remaining angle DEB. [Axiom 3.

In the same manner it may be shewn that the angle CEB is equal to the angle AED.

Wherefore, if two straight lines &c. q.e.d.

Corollary 1. From this it is manifest that, if two straight lines cut one another, the angles which they make at the point where they cut, are together equal to four right angles.

Corollary 2. And consequently, that all the angles made by any number of straight lines meeting at one point, are together equal to four right angles.

PROPOSITION 16. THEOREM.

If one side of a triangle be produced, the exterior angle shall be greater than either of the interior opposite angles.

Let ABC be a triangle, and let one side BC be produced to D: the exterior angle ACD shall be greater than either of the interior opposite angles CBA, BAC.

Bisect AC at E, [I. 10.

join BE and produce it to F, making EF equal to EB, [I. 3.

and join FC.

Because AE is equal to EC, and BE to EF; [Constr.

the two sides AE, EB are equal to the two sides CE, EF, each to each;

and the angle AEB is equal to the angle CEF,

because they are opposite vertical angles; [I. 15.

therefore the triangle AEB is equal to the triangle CEF, and the remaining angles to the remaining angles, each to each, to which the equal sides are opposite; [I. 4.

therefore the angle BAE is equal to the angle ECF.

But the angle ECD is greater than the angle ECF. [Axiom 9.

Therefore the angle ACD is greater than the angle BAE.

In the same manner if BC be bisected, and the side AC be produced to G, it may be shewn that the angle BCG, that is the angle ACD, is greater than the angle ABC. [I. 15.

Wherefore, if one side &c. q.e.d.

PROPOSITION 17. THEOREM.

Any two angles of a triangle are together less than two right angles.

Let ABC be a triangle: any two of its angles are together less than two right angles.

float

Produce BC to D.

Then because ACD is the exterior angle of the triangle ABC, it is greater than the interior opposite angle ABC. [I. 16.

To each of these add the angle ACB

Therefore the angles ACD, ACB are greater than the angles ABC ACB.

But the angles ACD, ACB are together equal to two right angles. [I. 13.

Therefore the angles ABC, ACB are together less than two right angles.

In the same manner it may be shewn that the angles BAC, ACB, as also the angles CAB, ABC, are together less than two right angles.

Wherefore, any two angles &c. q.e.d.

PROPOSITION 18. THEOREM.

The greater side of every triangle has the greater angle opposite to it.

Let ABC be a triangle, of which the side AC is greater than the side AB: the angle ABC is also greater than the angle ACB.

float

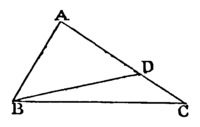
Because AC is greater than AB, make AD equal to AB, [I. 3.

and join BD.

Then, because ADB is the exterior angle of the triangle BDC, it is greater than the interior opposite angle DCB. [I. 16.

But the angle ADB is equal to the angle ABD, [I. 5.

because the side AD is equal to the side AB. [Constr.

Therefore the angle ABD is also greater than the angle ACB.

Much more then is the angle ABC greater than the angle ACB. [Axiom 9.

Wherefore, the greater side &c. q.e.d.

PROPOSITION 19. THEOREM.

The greater angle of every triangle is subtended by the greater side, or has the greater side opposite to it.

Let ABC be a triangle, of which the angle ABC is greater than the angle ACB: the side AC is also greater than the side AB.

float

For if not, AC must be either equal to AB or less than AB.

But AC is not equal to AB,

for then the angle ABC would be equal to the angle ACB; [I. 5.

but it is not; [Hypothesis.

therefore AC is not equal to AB. Neither is AC less than AB,

for then the angle ABC would be less than the angle ACB; [I. 18.

but it is not; [Hypothesis.

therefore AC is not less than AB.

And it has been shewn that AC is not equal to AB.

Therefore AC is greater than AB.

Wherefore, the greater angle &c. q.e.d.

PROPOSITION 20. THEOREM.

Any two sides of a triangle are together greater than the third side.

float

Let ABC be a triangle: any two sides of it are together greater than the third side; namely, BA, AC greater than BC; and AB, BC greater than AC; and BC, CA greater than AB.

Produce BA to D,

making AD equal to AC, [I. 3.

and join DC.

Then, because AD is equal to AC, [Construction.

the angle ADC is equal to the angle ACD. [I. 5.

But the angle BCD is greater than the angle ACD. [Ax. 9.

Therefore the angle BCD is greater than the angle BDC.

And because the angle BCD of the triangle BCD is greater than its angle BDC, and that the greater angle is subtended by the greater side; [I. 19.

therefore the side BD is greater than the side BC.

But BD is equal to BA and AC.

Therefore BA, AC are greater than BC.

In the same manner it may be shewn that AB, BC are greater than AC, and BC, CA greater than AB.

Wherefore, any two sides &c. q.e.d.

PROPOSITION 21. THEOREM.

If from the ends of the side of a triangle there be drawn two straight lines to a point within the triangle, these shall be less than the other two sides of the triangle, but shall contain a greater angle.

float

Let ABC be a triangle, and from the points B, C, the ends of the side BC, let the two straight lines BD, CD be drawn to the point D within the triangle: BD, DC shall be less than the other two sides BA, AC of the triangle, but shall contain an angle BDC greater than the angle BAC.

Produce BD to meet AC at E.

Because two sides of a triangle are greater than the third side, the two sides BA, AE of the triangle ABE are greater than the side BE. [I. 20.

To each of these add EC.

Therefore BA, AC are greater than BE, EC.

Again; the two sides CE, ED of the triangle CED are greater than the third side CD. [I. 20.

To each of these add DB.

Therefore CE, EB are greater than CD, DB.

But it has been shewn that BA, AC are greater than BE, EC;

much more then are BA, AC greater than BD, DC.

Again, because the exterior angle of any triangle is greater than the interior opposite angle, the exterior angle BDC of the triangle CDE is greater than the angle CED. [I. 16.

For the same reason, the exterior angle CEB of the triangle ABE is greater than the angle BAE.

But it has been shewn that the angle BDC is greater than the angle CEB;

much more then is the angle BDC greater than the angle BAC.

Wherefore, if from the ends &c. q.e.d.

PROPOSITION 22. PROBLEM.

To make a triangle of which the sides shall be equal to three given straight lines, but any two whatever of these must be greater than the third.

Let A, B, C be the three given straight lines, of which any two whatever are greater than the third; namely, A and B greater than C; A and C greater than B; and B and C greater than A: it is required to make a triangle of which the sides shall be equal to A, B, C, each to each.

float

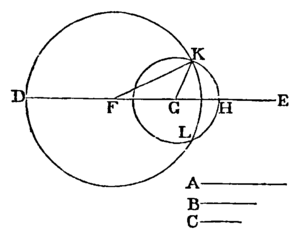
Take a straight line DE terminated at the point D, but unlimited towards E, and make DF equal to A, FG equal to B, and GH equal to C. [I. 3.

From the centre F, at the distance FD, describe the circle DKL. [Post. 3.

From the centre G, at the distance GH, describe the circle HLK, cutting the former circle at K.

Join KF, KG. The triangle KFG shall have its sides equal to the three straight lines A,B, C.

Because the point F is the centre of the circle DKL, FD is equal to FK. [Definition 15.

But FD is equal to A. [Construction.

Therefore FK is equal to A. [Axiom 1.

Again, because the point G is the centre of the circle HLK, GH is equal to GK [Definition 15.

But GH is equal to C. [Construction.

Therefore GK is equal to C. [Axiom 1.

And FG is equal to B. [Construction.

Therefore the three straight lines KF, FG, GK are equal to the three A, B, C.

Wherefore the triangle KFG has its three sides KF, FG, GK equal to the three given straight lines A, B, C. q.e.f.

PROPOSITION 23. PROBLEM.

At a given point in a given straight line, to make a rectilineal angle equal to a given rectilineal angle.

float

Let AB be the given straight line, and A the given point in it, and DCE the given rectilineal angle: it is required to make at the given point A, in the given straight line AB, an angle equal to the given rectilineal angle DCE.

In CD, CE take any points D, E, and join DE.

Make the triangle AFG the sides of which shall be equal to the three straight lines CD, DE, EC; so that AF shall be equal to CD, AG to CE, and FG to DE. [I. 22.

The angle FAG shall be equal to the angle DCE.

Because FA, AG are equal to DC, CE, each to each, and the base FG equal to the base DE; [Construction.

therefore the angle FAG is equal to the angle DCE. [I. 8.

Wherefore at the given point A in the given straight line AB, the angle FAG has been made equal to the given rectilineal angle DCE. q.e.f.

PROPOSITION 24. THEOREM.

If two triangles have two sides of the one equal to two sides of the other, each to each, but the angle contained by the two sides of one of them greater than the angle contained by the two sides equal to them, of the other, the base of that which has the greater angle shall be greater than the base of the other.

Let ABC, DEF be two triangles, which have the two sides AB, AC, equal to the two sides DE, DF, each to each, namely, AB to DE, and AC to DF, but the angle BAC greater than the angle EDF: the base BC shall be

float

greater than the base EF.

Of the two sides DE, DF, let DE be the side which is not greater than the other. At the point D in the straight line DE, make the angle EDG equal to the angle BAC, [I. 23.

and make DG equal to AC or DF, [I. 3.

and join EG, GF.

Because AB is equal to DE, [Hypothesis.

and AC to DG; [Construction.

the two sides BA, AC are equal to the two sides ED, DG, each to each;

and the angle BAC is equal to the angle EDG; [Constr.

therefore the base BC is equal to the base EG. [I. 4.

And because DG is equal to DF, [Construction.

the angle DGF is equal to the angle DFG. [I. 5.

But the angle DGF is greater than the angle EGF. [Ax. 9.

Therefore the angle DFG is greater than the angle EGF. Much more then is the angle EFG greater than the angle EGF. [Axiom 9.

And because the angle EFG of the triangle EFG is greater than its angle EGF, and that the greater angle is subtended by the greater side, [I. 19.

therefore the side EG is greater than the side EF.

But EG was shewn to be equal to BC;

therefore BC is greater than EF.

Wherefore, if two triangles &c. q.e.d.

PROPOSITION 25. THEOREM.

If two triangles have two sides of the one equal to two sides of the other, each to each, but the base of the one

greater than the base of the other, the angle contained by the sides of that which has the greater base, shall be greater than the angle contained by the sides equal to them, of the other.

Let ABC, DEF be two triangles, which have the two sides AB, AC equal to the two sides DE, DF, each to each, namely, AB to DE, and AC to DF, but the base BC greater than the base EF: the angle BAC shall be greater than the angle EDF.

float

For if not, the angle BAC must be either equal to the angle EDF or less than the angle EDF.

But the angle BAC is not equal to the angle EDF, for then the base BC would be equal to the base EF; [I. 4.

but it is not; [Hypothesis.

therefore the angle BAC is not equal to the angle EDF.

Neither is the angle BAC less than the angle EDF,

for then the base BC would be less than the base EF; [I. 24.

but it is not; [Hypothesis.

therefore the angle BAC is not less than the angle EDF.

And it has been shewn that the angle BAC is not equal to the angle EDF.

Therefore the angle BAC is greater than the angle EDF.

Wherefore, if two triangles &c. q.e.d.

PROPOSITION 26. THEOREM.

If two triangles have two angles of the one equal to two angles of the other, each to each, and one side equal to one side, namely, either the sides adjacent to the equal angles, or sides which are opposite to equal angles in each, then shall the other sides be equal, each to each, and also the third angle of the one equal to the third angle of the other.

Let ABC, DEF be two triangles, which have the angles ABC, BCA equal to the angles DEF, EFD, each

to each, namely, ABC to DEF, and BCA to EFD; and let them have also one side equal to one side; and first let those sides be equal which are adjacent to the equal angles in the two triangles, namely, BC to EF: the other sides shall be equal, each to each, namely, AB to DE, and AC to DF, and the third angle BAC equal to the third angle EDF.

float

For if AB be not equal to DE, one of them must be greater than the other. Let AB be the greater, and make BG equal to DE, [I. 3.

and join GC.

Then because GB is equal to DE, [Construction.

and BC to EF; [Hypothesis.

the two sides GB, BC are equal to the two sides DE, EF, each to each;

and the angle GBC is equal to the angle DEF; [Hypothesis.

therefore the triangle GBC is equal to the triangle DEF, and the other angles to the other angles, each to each, to which the equal sides are opposite; [I. 4.

therefore the angle GCB is equal to the angle DFE.

But the angle DFE is equal to the angle ACB. [Hypothesis.

Therefore the angle GCB is equal to the angle ACB, [Ax. 1.

the less to the greater; which is impossible.

Therefore AB is not unequal to DE,

that is, it is equal to it;

and BC is equal to EF; [Hypothesis.

therefore the two sides AB, BC are equal to the two sides DE, EF, each to each;

and the angle ABC is equal to the angle DEF; [Hypothesis.

therefore the base AC is equal to the base DF, and the third angle BAC to the third angle EDF. [I. 4.

Next, let sides which are opposite to equal angles in each triangle be equal to one another, namely, AB to DE: likewise in this case the other sides shall be equal, each to each, namely, BC to EF, and AC to DF, and also the third angle BAC equal to the third angle EDF.

float

For if BC be not equal to EF, one of them must be greater than the other.
Let BC be the greater, and make BH equal to EF, [I. 3.
and join AH.

Then because BH is equal to EF, [Construction.
and AB to DE; [Hypothesis.
the two sides AB, BH are equal to the two sides DE, EF, each to each;
and the angle ABH is equal to the angle DEF; [Hypothesis.
therefore the triangle ABH is equal to the triangle DEF, and the other angles to the other angles, each to each, to which the equal sides are opposite; [I. 4.
therefore the angle BHA is equal to the angle EFD.
But the angle EFD is equal to the angle BCA. [Hypothesis.
Therefore the angle BHA is equal to the angle BCA; [Ax. 1.
that is, the exterior angle BHA of the triangle AHC is equal to its interior opposite angle BCA;
which is impossible. [I. 16.
Therefore BC is not unequal to EF,
that is, it is equal to it;
and AB is equal to DE; [Hypothesis.
therefore the two sides AB, BC are equal to the two sides DE, EF, each to each;
and the angle ABC is equal to the angle DEF; [Hypothesis.
therefore the base AC is equal to the base DF, and the third angle BAC to the third angle EDF. [I. 4.

Wherefore, if two triangles &c. q.e.d.

PROPOSITION 27. THEOREM.

If a straight line falling on two other straight lines, make the alternate angles equal to one another, the two straight lines shall be parallel to one another.

Let the straight line EF, which falls on the two straight lines AB, CD, make the alternate angles AEF, EFD equal to one another: AB shall be parallel to CD.

For if not, AB and CD, being produced, will meet either towards B, D or towards A, C. Let them be pro- duced and meet towards B, D at the point G.

Therefore GEF is a triangle, and its exterior angle AEF is greater than the interior opposite angle EFG; [I. 16.
But the angle AEF is also equal to the angle EFG; [Hyp.
which is impossible.
Therefore AB and CD being produced, do not meet to- wards B, D.

In the same manner, it may be shewn that they do not meet towards A, C.
But those straight lines which being produced ever so far both ways do not meet, are parallel. [Definition 35.
Therefore AB is parallel to CD.

Wherefore, if a straight line &c. q.e.d.

PROPOSITION 28. THEOREM.

If a straight line falling on two other straight lines, make the exterior angle equal to the interior and opposite angle on the same side of the line, or make the interior angles on the same side together equal to two right angles, the two straight lines shall be parallel to one another. Let the straight line EF, which falls on the two straight lines AB, CD, make the exterior angle EGB equal to the interior and opposite angle GHD on the same side, or make the interior angles on the same side BGH, GHD together equal to two right angles : AB shall be parallel to CD.

Because the angle EGB is equal to the angle GHD, [I. 15.
and the angle EGB is also equal to the angle AGH, [1.15.
therefore the angle AGH is equal to the angle GHD;[Ax.l.
and they are alternate angles ;
therefore AB is parallel to CD. [I. 27.

Again; because the angles BGH, GHD are together equal to two right angles, [Hypothesis.
and the angles AGH, BGH are also together equal to two right angles, [1. 13.
therefore the angles AGH, BGH are equal to the angles BGH, GHD. Takeaway the common angle BGH; therefore the remaining angle AGH is equal to the remaining angle GHD; [Axiom 3. and they are alternate angles ; therefore AB is parallel to CD. [I. 27.

Wherefore, if a straight line &c. q.e.d.

PROPOSITION 29. THEOREM.

If a straight line fall on two parallel straight lines, it makes the alternate angles equal to one another, and the exterior angle equal to the interior and opposite angle on the same side; and also the two interior angles on the same side together equal to two right angles.

Let the straight line EF fall on the two parallel straight lines AB, CD : the alternate angles AGH, GHD shall be equal to one another, and the exterior angle EGB shall be equal to the interior and opposite angle on the same side, GHD, and the two interior angles on the same side, BGH, GHD, shall be together equal to two right angles.

For if the angle AGH be not equal to the angle GHD, one of them must be greater than the other ; let the angle AGH be the greater.
Then the angle AGH is greater than the angle GHD ;
to each of them add the angle BGH;
therefore the angles AGH, BGH are greater than the angles BGH, GHD.
But the angles AGH, BGH are together equal to two right angles ; [I. 13.
therefore the angles BGH, GHD are together less than two right angles.
But if a straight line meet two straight lines, so as to make the two interior angles on the same side of it, taken together, less than two right angles, these straight lines being continually produced, shall at length meet on that side on which are the angles which are less than two right angles. [Axiom 12.
Therefore the straight lines AB, CD, if continually pro- duced, will meet.
But they never meet, since they are parallel by hypothesis.
Therefore the angle AGH is not unequal to the angle GHD ; that is, it is equal to it.

But the angle AGH is equal to the angle EGB. [I. 15.
Therefore the angle EGB is equal to the angle GHD. [Ax. 1 .

Add to each of these the angle BGH.
Therefore the angles EGB, BGH are equal to the angles BGH, GHD. [Axiom 2.
But the angles EGB, BGH are together equal to two right angles. [I. 13.
Therefore the angles BGH, GHD are together equal to two right angles. [Axiom 1.

Wherefore, if a straight line &c. q.e.d.

PROPOSITION 30. THEOREM.

Straight lines which are parallel to the same straight line are parallel to each other.

Let AB, CD be each of them parallel to EF: AB shall be parallel to CD.

Let the straight line GHK cut AB, EF, CD.

Then, because GHK cuts the parallel straight lines AB, EF, the angle AGH is equal to the angle GHF. [I. 29.
Again, because GK cuts the parallel straight lines EF, CD, the angle GHF is equal to the angle GKD. [I. 29.
And it was shewn that the angle AGK is equal to the angle GHF.
Therefore the angle AGK is equal to the angle GKD;[Ax. 1. and they are alternate angles ;
therefore AB is parallel to CD.

Wherefore, straight lines &c. q.e.d.

PROPOSITION 31. PROBLEM.

To draw a straight line through a given point parallel to a given straight line.

Let A be the given point, and BC the given straight line : it is required to draw a straight line through the point A parallel to the straight line BC. In BC take any point D, and join AD ; at the point A in the straight line AD, make the angle DAE equal to the angle ADC, [I.23.
and produce the straight line EA to F. EF shall be parallel to BC. Because the straight line AD which meets the two straight lines BC, EF, makes the alternate angles BAD, ADC equal to one another, [Construction.
EF is parallel to BC. [I. 27.

Wherefore the straight line EAF is drawn through the given point A, parallel to the given straight line BC. q.e.f.

PROPOSITION 32. THEOREM.

If a side of any triangle be produced, the exterior angle is equal to the two interior and opposite angles; and the three interior angles of every triangle are together equal to two right angles.

Let ABC be a triangle, and let one of its sides BC be produced to D : the exterior angle ACD shall be equal to the two interior and opposite angles CAB,ABC; and the three interior angles of the triangle, namely, ABC, BCA, CAB shall be equal to two right angles.

Through the point C draw CE parallel to AB. [1.31.

Then, because AB is par- allel to CE, and AC falls on them, the alternate angles BAC, ACE are equal. [I. 29.
Again, because AB is parallel to CE, and BD falls on them, the exterior angle ECD is equal to the interior and opposite angle ABC. [I. 29.
But the angle ACE was shewn to be equal to the angle BAC;
therefore the whole exterior angle ACD is equal to the two interior and opposite angles CAB, ABC. [Axiom 2.

To each of these equals add the angle ACB;
therefore the angles ACD, ACB are equal to the three angles CBA, BAC, ACB. [Axiom 2.
But the angles ACD, ACB are together equal to two right angles ; [I. 13.
Therefore also the angles CBA, BAC, ACB are together equal to two right angles. [Axiom 1.

Wherefore, if a side of any triangle &c. q.e.d. Corollary 1. All the interior angles of any recti-lineal figure, together with four right angles, are equal to twice as many right angles as the figure has sides.

For any rectilineal figure ABCDE can be divided into as many triangles as the figure has sides, by drawing; straight lines from a point F within the figure to each of its angles.

And by the preceding proposition, all the angles of these triangles are equal to twice as many right angles as there are triangles, that is, as the figure has sides.
And the same angles are equal to the interior angles of the figure, together with the angles at the point F, which is the common vertex of the triangles, that is, together with four right angles. [I. 15. Corollary 2.
Therefore all the interior angles of the figure, together with four right angles, are equal to twice as many right angles as the figure has sides.

Corollary 2. All the exterior angles of any recti-lineal figure are together equal to four right angles.

Because every interior angle ABC, with its adjacent exterior angle ABD, is equal to two right angles ; [I. 13.
therefore all the interior angles of the figure, together with all its exterior angles, are equal to twice as many right angles as the figure has sides.
But, by the foregoing Corollary all the interior angles of the figure, together with four right angles, are equal to twice as many right angles as the figure has sides.
Therefore all the interior angles of the figure, together with all its exterior angles, are equal to all the interior angles of the figure, together with four right angles.
Therefore all the exterior angles are equal to four right;

angles.

PROPOSITION 33. THEOREM.

The straight lines which join the extremities of two equal and parallel straight lines towards the same parts, are also themselves equal and parallel.

Let AB and CD be equal and parallel straight lines, and let them be joined towards the same parts by the straight lines AC and BD : AC and BD shall be equal and parallel.

Join BC.

Then because AB is par- allel to CD, [Hypothesis.
and BC meets them, the alternate angles ABC, BCD are equal. [I. 29.
And because AB is equal to CD, [Hypothesis. and BC is common to the two triangles ABC, DCB ;
the two sides AB, BC are equal to the two sides DC, CB, each to each ;
and the angle ABC was shewn to be equal to the angle BCD;
therefore the base AC is equal to the base BD, and the triangle ABC to the triangle BCD, and the other angles to the other angles, each to each, to which the equal sides are opposite ; [I. 4.
therefore the angle ACB is equal to the angle CBD.

And because the straight line BC meets the two straight lines AC, BD, and makes the alternate angles ACB, CBD equal to one another, AC is parallel to BD, [I. 27.
And it was shewn to be equal to it.

Wherefore, the straight lines &c. q.e.d.

PROPOSITION 34. THEOREM.

The opposite sides and angles of a parallelogram are equal to one another, and the diameter bisects the par- allelogram, that is, divides it into two equal parts.

Note. A parallelogram is a four-sided figure of which the opposite sides are parallel ; and a diameter is the straight line joining two of its opposite angles. Let ACDB be a parallelogram, of which BC is a diameter; the opposite sides and angles of the figure shall be equal to one another, and the diameter BC shall bisect it.

Because AB is parallel to CD, and BC meets them, the alternate angles ABC, BCD are equal to one another. [I. 29.
And because AC is parallel to BD, and BC meets them, the alternate angles ACB, CBD are equal to one another. [I. 29.
Therefore the two triangles ABC, BCD have two angles ABC, BCA in the one, equal to two angles DCB, CBD in the other, each to each, and one side BC is common to the two triangles, which is adjacent to their equal angles;
therefore their other sides are equal, each to each, and the third angle of the one to the third angle of the other, namely, the side AB equal to the side CD, and the side AC equal to the side BD, and the angle BAC equal to the angle CDB. [I. 26.
And because the angle ABC is equal to the angle BCD and the angle CBD to the angle ACB, the whole angle ABD is equal to the whole angle ACD. [Ax. 2.
And the angle BAC has been shewn to be equal to the angle CDB.
Therefore the opposite sides and angles of a parallelogram are equal to one another.
Also the diameter bisects the parallelogram.
For AB being equal to CD, and BC common,
the two sides AB, BC are equal to the two sides DC, CB each to each;
and the angle ABC has been shewn to be equal to the angle BCD;
therefore the triangle ABC is equal to the triangle BCD, [1. 4.
and the diameter BC divides the parallelogram ACDB into two equal parts.

Wherefore, the opposite sides &c. q.e.d.

PROPOSITION 35. THEOREM.

Parallelograms on the same base, and between the same parallels, are equal to one another.

Let the parallelograms ABCD, EBCF be on the same base BC, and between the same parallels AF, BC : the paral- lelogram ABCD shall be equal to the parallelogram EBCF.

If the sides AD, EF of the parallelograms ABCD, EBCF, opposite to the base BC, be terminated at the same point D, it is plain that each of the parallelograms is double of the triangle BDC; [I. 34.
and they are therefore equal to one another. [Axiom 6.

But if the sides AD, EF, opposite to the base BC of the parallelo- grams ABCD, EBCF be not terminated at the same point, then, because ABCD is a par- allelogram AD is equal to BC ; [I. 34.
for the same reason EF is, equal to BC ;
therefore AD is equal to EF; [Axiom 1.
therefore the whole, or the remainder, AE is equal to the whole, or the remainder, DF. [Axioms 2, 3.
And AB is equal to DC ; [I. 34.
therefore the two sides EA, AB are equal to the two sides FD,DC each to each;
and the exterior angle FDC is equal to the interior and opposite angle EAB ; [I. 29.
therefore the triangle EAB is equal to the triangle FDC. [I. 4.

Take the triangle FDC from the trapezium ABCF, and from the same trapezium take the triangle EAB, and the remainders are equal ; [Axiom 3.
that is, the parallelogram ABCD is equal to the parallelo-gram EBCF.

Wherefore, parallelograms on the same base &c. q.e.d.

PROPOSITION 36. THEOREM.

Parallelograms on equal bases, and between the same parallels are equal to one another.

Let ABCD, EFGH be parallelograms on equal bases BC, FG and between the same parallels AH, BG: the parallelogram ABCD shall be equal to the parallelogram EFGH.

Join BE, CH.

Then, because BC is equal to FG, [Hyp.
and FG to EH,[I.34.
BC is equal to EH; [Axiom 1.
and they are parallels, - [Hypothesis.
and joined towards the same parts by the straight lines BE, CH.

But straight lines which join the extremities of equal and parallel straight lines towards the same parts are them- selves equal and parallel. [I. 33.
Therefore BE, CH are both equal and parallel. Therefore EBCH is a parallelogram. [Definition.
And it is equal to ABCD, because they are on the same base BC, and between the same parallels BC,AH. [I. 35.

For the same reason the parallelogram EFGH is equal to the same EBCH.
Therefore the parallelogram ABCD is equal to the par- allelogram EFGH. [Axiom l.

Wherefore, parallelograms &c. q.e.d.

PROPOSITION 37. THEOREM.

Triangles on the same base, and between the same parallels, are equal.

Let the triangles ABC, DBC be on the same base BC, and between tie same parallels AD,BC the tri- angle ABC shall be equal to the triangle DBC.

Produce AD both ways to the points E, F ; [Post. 2.
through B draw BE parallel to CA, and through C draw CF parallel to BD. [I. 31.

Then each of the figures EBCA, DBCF is a parallelo- gram ; [Definition. and EBCA is equal to DBCF, because they are on the same base BC, and between the same parallels BG, EF. [I. 35.
And the triangle ABC is, half of the parallelogram EBCA, because the diameter AB bisects the parallelogram ; [I. 34.
and the triangle DBC is half of the parallelogram DBCF, because the diameter DC bisects the parallelogram. [I. 34.
But the halves of equal things are equal. [Axiom 7.
Therefore the triangle ABC is equal to the triangle DBC. Wherefore, triangles &c. q.e.d.

PROPOSITION 38. THEOREM.

Triangles on equal bases, and between the same parallels, are equal to one another.

Let the triangles ABC, DEF be on equal bases BC, EF, and between the same parallels BF, AD : the triangle ABC shall be equal to the triangle DEF,

Produce AD both ways to the points G,H;
through B draw BG parallel to CA, and through F draw FH parallel to ED.[I.31.
Then each of the figures GBCA, DEFH is a parallelogram. [Definition.
And they are equal to one another because they are on equal bases BC, EF, and between the same parallels BF, GH. [1. 36.
And the triangle ABC is half of the parallelogram GBCA, because the diameter AB bisects the parallelogram ;[I. 34.
and the triangle DEF is half of the parallelogram DEFH, because the diameter DF bisects the parallelogram.
But the halves of equal things are equal. [Axiom 7.
Therefore the triangle ABC is equal to the triangle DEF.

Wherefore, triangles &c. q.e.d.

PROPOSITION 39. THEOREM.

Equal triangles on the same base, and on the same side of it, are between the same parallels.

Let the equal triangles ABC, DBC be on the same base BC, and on the same side of it : they shall be between the same parallels.

Join AD.
AD shall be parallel to BC.

For if it is not, through A draw AE parallel to BC, meeting BD at E. [I. 31.
and join EC.
Then the triangle ABC is equal to the triangle EBC, because they are on the same base BC, and between the same parallels BC, AE. [I. 37.
But the triangle ABC is equal to the triangle DBC.[Hyp. Therefore also the triangle DBC is equal to the triangle EBC, [Axiom 1.
the greater to the less ; which is impossible.
Therefore AE is not parallel to BC.

In the same manner it can be shewn, that no other straight line through A but AD is parallel to BC;
therefore AD is parallel to BC.

Wherefore, equal triangles &c., q.e.d.

PROPOSITION 40. THEOREM.

Equal triangles, on equal bases, in the same straight line, and on the same side of it, are between the same parallels.

Let the equal triangles ABC, DEF be on equal bases BC, EF, in the same straight line BF, and on the same side of it: they shall be between the same parallels.

Join AD.
AD shall be parallel to BF.

For if it is not, through A draw AG parallel to BF,
meeting ED at G [I. 31.
and join GF.
Then the triangle ABC is equal to the triangle GEF, because they are on equal bases BC, EF, and between the same parallels, [I. 38.
But the triangle ABC is equal to the triangle DEF. [Hyp.
Therefore also the triangle DEF is equal to the triangle GEF, [Axiom 1.
the greater to the less ; which is impossible.
Therefore AD is not parallel to BF,

In the same manner it can be shewn that no other straight line through A but AD parallel to BF; therefore AD is parallel to BF,

Wherefore, equal triangles &c. q.e.d.

PROPOSITION 41. THEOREM.

If a parallelogram and a triangle he on the same base and between the same parallels, the parallelogram, shall be double of the triangle.

Let the parallelogram ABCD and the triangle EBC be on the same base BC, and between the same parallels BC, AE : the parallelogram ABCD shall be double of the triangle EBC.

Join AC.

Then the triangle ABC is equal to the triangle EBC because they are on the same base BC, and between the same parallels BC, AE. [I. 37.
But the parallelogram ABCD is double of the triangle ABC,
because the diameter AC bisects the parallelogram. [I . 34.
Therefore the parallelogram ABCD is also double of the triangle EBC.

Wherefore, if a parallelogram &c. q.e.d.

PROPOSITION 42. PROBLEM.

To describe a parallelogram that shall be equal to a given triangle and have one of its angles equal to a given rectilineal angle.

Let ABC be the given triangle, and D the given recti- lineal angle : it is required to describe a parallelogram that shall be equal to the given triangle ABC, and have one of its angles equal to D.

Bisect BC at E:[I.10.
join AE, and at the point E, in the straight line EC, make the angle CEF equal to D; [I.23.
through A draw AFG parallel to EC, and through C draw CG parallel to EF. [I. 31.
Therefore FECG is a parallelogram. [Definition.

And, because BE is equal to EC, [Construction. the triangle ABE is equal to the triangle AEC, because they are on equal bases BE, EC, and between the same parallels BC, AG. [I. 38.
Therefore the triangle ABC is double of the triangle AEC.
But the parallelogram FECG is also double of the triangle AEC, because they are on the same base EC, and between the same parallels EC, AG. [I. 41.
Therefore the parallelogram FECG is equal to the triangle ABC ; [Axiom 6.
and it has one of its angles CEF equal to the given angle D. [Construction.

Wherefore a parallelogram FECG has been described equal to the given triangle ABC, and having one of its angles CEF equal to the given angle D. q.e.f.

PROPOSITION 43. THEOREM.

The complements of the parallelograms which are about the diameter of any parallelogram are equal to one another.

Let ABCD be a parallelogram, of which the diameter is AC; and EH, GF parallelograms about AC, that is, through which AC passes ; and BK, KD the other parallelograms which make up the whole figure ABCD, and which are therefore called the complements: the complement BK shall be equal to the complement KD.

Because ABCD is a parallelogram, and AC its diameter, the triangle ABC is equal to the triangle ADC. [I. 34.
Again, because AEKH is a parallelogram, and AK its diameter, the triangle AEK is equal to the triangle AHK. [I. 34.
For the same reason the triangle KGC is equal to the triangle KFC. Therefore, because the triangle AEK is equal to the triangle AHK, and the triangle KGC to the triangle KFC ;
the triangle AEK together with the triangle KGC is equal to the triangle AHK together with the triangle KFC. [Ax. 2.
But the whole triangle ABC was shewn to be equal to the whole triangle ADC.

Therefore the remainder, the complement BK, is equal to the remainder, the complement KD. [Axiom 3,

Wherefore, the complements &c. q.e.d.

PROPOSITION 44. PROBLEM.

To a given straight line to apply a parallelogram, which shall be equal to a given triangle, and have one of its angles equal to a given rectilineal angle. Let AB be the given straight line, and C the given triangle, and D the given rectilineal angle : it is required to apply to the straight line AB a parallelogram equal to the triangle C, and having an angle equal to D.

Make the parallelogram BEFG equal to the triangle C, and having the angle EBG equal to the angle D, so that BE may be in the same straight line with AB ; [I. 42.
produce FG to H ;
through A draw AH parallel to BG or EF, [I. 31.
and join HB. [I. 31.
Then, because the straight line HF falls on the parallels AH, EF, the angles AHF, HFE are together equal to two right angles. [I. 29.
Therefore the angles BHF, HFE are together less than two right angles.
But straight lines which with another straight line make the interior angles on the same side together less than two right angles will meet on that side, if produced far enough. [Ax. 12.
Therefore HB and FE will meet if produced ;
let them meet at K.
Through K draw KL parallel to EA or FH ; [I. 31.

and produce HA, GB to the points L, M.

Then HLKF is a parallelogram, of which the diameter is HK; and AG, ME are parallelograms about HK; and LB, BF are the complements.
Therefore LB is equal to BF. [I. 43.
But BF is equal to the triangle C [Construction.</br.> Therefore LB is equal to the triangle C [Axiom 1.
And because the angle GBE is equal to the angle ABM, [I.15.
and likewise to the angle D ; [Construction.

the angle ABM is equal to the angle D. [Axiom 1.

Wherefore to the given straight line AB the parallelogram LB is applied, equal to the triangle C, and having the angle ABM equal to the angle D. q.e.f.

PROPOSITION 45. PROBLEM.

To describe a parallelogram equal to a given rectilineal figure, and having an angle equal to a given rectilineal angle.

Let ABCD be the given rectilineal figure, and E the given rectilineal angle: it is required to describe a par- allelogram equal to ABCD, and having an angle equal to E.

Join DB, and describe the parallelogram FH equal to the triangle ADB, and having the angle FKH equal to the angle E ; [I. 42.
and to the straight line GH apply the parallelogram GM equal to the triangle DBC, and having the angle GHM equal to the angle E. [I. 44.

The figure FKML shall be the parallelogram required. Because the angle E is equal to each of the angles FKH, GHM, [Construction.
the angle FKH is, equal to the angle GHM. [Axiom 1.
Add to each of these equals the angle KHG ;
therefore the angles FKH, KHG are equal to the angles KHG,GHM. [Axiom 2.
But FKH, KHG are together equal to two right angles;[I.29.
therefore KHG,GHM are together equal to two right angles.

And because at the point H in the straight line GH, the two straight lines KH, HM, on the opposite sides of it, make the adjacent angles together equal to two right angles, KH is in the same straight line with HM. [I. 14.

And because the straight line HG meets the parallels KM, FG, the alternate angles MHG, HGF are equal. [I. 29.
Add to each of these equals the angle HGL ;
therefore the angles MHG, HGL, are equal to the angles HGF, HGL. [Axiom 2.
But MHG,HGL are together equal to two right angles; [I. 29.
therefore HGF, HGL are together equal to two right angles. Therefore FG is in the same straight line with GL. [I. 14.

And because KF is parallel to HG, and HG to ML,[Constr.
KF is parallel to ML ; [I. 30.
and KM, FL are parallels ; [Construction.
therefore KFLM a parallelogram. [Definition.

And because the triangle ABD is equal to the parallelo- gram HF, [Construction.
and the triangle DBC to the parallelogram GM ; [Constr. the whole rectilineal figure ABCD is equal to the whole parallelogram KFLM. [Axiom 2.

Wherefore, the parallelogram KFLM has been de- scribed equal to the given rectilineal figure ABCD, and having the angle FKM equal to the given angle E. q.e.f.

Corollary. From this it is manifest, how to a given straight line, to apply a parallelogram, which shall have an angle equal to a given rectilineal angle, and shall be equal to a given rectilineal figure ; namely, by applying to the given straight line a parallelogram equal to the first tri- angle ABD, and having an angle equal to the given angle;

and so on. [I. 44.

PROPOSITION 46. PROBLEM.

To describe a square on a given straight line.

Let AB be the given straight line : it is required to describe a square on AB.

From the point A draw AC at right angles to AB; [I. 11.
and make AD equal to AB; [I. 3.
through D draw DE parallel to AB ; and through B draw BE parallel to AD. [I. 31.
ADEB shall be a square.

For ADEB is by construction a parallelogram ;
therefore AB is equal to DE and AD to BE. [I. 34.
But AB is equal to AD. [Construction. Therefore the four straight lines BA,AD, DE, EB are equal to one another, and the parallelogram ADEB is equilateral. [Axiom 1.

Likewise all its angles are right angles.
For since the straight line AD meets the parallels AB,DE, the angles BAD, ADE are together equal to two right angles ; [I. 29.
but BAD is a right angle ; [Construction.
therefore also ADE is a right angle. [Axiom 3.
But the opposite angles of parallelograms are equal. [I. 34.
Therefore each of the opposite angles ABE, BED is a right angle. [Axiom 1.

Therefore the figure ADEB is rectangular; and it has been shewn to be equilateral. Therefore it is a square. [Definition, 30. And it is described on the given straight line AB. q.e.f.

Corollary. From the demonstration it is manifest that every parallelogram which has one right angle has all its

angles right angles.

PROPOSITION 47. THEOREM.

In any right-angled triangle, the square which is de-scribed on the side subtending the right angle is equal to the squares described on the sides which contain the right angle.

Let ABC be a right-angled triangle, having the right angle BAC : the square described on the side BC shall be equal to the squares described on the sides BA, AC.

On BC describe the square BDEC, and on BA, AC de- scribe the squares GB,HC; [I.46.
through A draw AL parallel to BD or CE ; [I. 31.
and join AD, FC.

Then, because the angle BAC is a right angle, [Hypothesis.

and that the angle BAG is also a right angle, [Definition 30.
the two straight lines AC, AG, on the opposite sides of AB, make with it at the point A the adjacent angles equal to two right angles ;
therefore CA is in the same straight line with AG. [I, 14.
For the same reason, AB and AH are in the same straight line.

Now the angle DBC is equal to the angle FBA, for each of them is a right angle. [Axiom 11.
Add to each the angle ABC.
Therefore the whole angle DBA is equal to the whole angle FBC. [Axiom 2.
And because the two sides AB, BD are equal to the two sides FB, BC, each to each ; [Definition 30.
and the angle DBA is equal to the angle FBC;
therefore the triangle ABD is equal to the triangle FBC. [I. 4.
Now the parallelogram BL is double of the triangle ABD, because they are on the same base BD, and between the same parallels BD, AL. [I. 41.
And the square GB is double of the triangle FBC, because they are on the same base FB, and between the same parallels FB, GC. [I. 41.
But the doubles of equals are equal to one another. [Ax. 6.
Therefore the parallelogram BL is equal to the square GB.

In the same manner, by joining AE, BK, it can be shewn, that the parallelogram CL is equal to the square CH.
Therefore the whole square BDEC is equal to the two squares GB, HC. [Axiom 2.
And the square BDEC is described on BC, and the squares GB,HC on BA,AC
Therefore the square described on the side BC is equal to the squares described on the sides BA, AC.

Wherefore, in any right-angled triangle &c. q.e.d.

PROPOSITION 48. THEOREM.

If the square described on one of the sides of a tri-angle be equal to the squares described on the other two sides of it, the angle contained by these two sides is a right angle.

Let the square described on BC, one of the sides of the triangle ABC, be equal to the squares described on the other sides BA, AC: the angle BAC shall be a right angle.

From the point A draw AD at right angles to AC ; [I. 11.
and make AD equal to BA; [I. 3.
and join DC.

Then because DA is equal to BA, the square on DA is equal to the square on BA.
To each of these add the square on AC.
Therefore the squares on DA, AC are equal to the squares on BA,AC [Axiom 2.
But because the angle DAC is a right angle, [Construction.
the square on DC is equal to the squares on DA, AC. [I. 47.
And, by hypothesis, the square on BC is equal to the squares on BA, AC.
Therefore the square on DC is equal to the square on BC. [Ax 1.
Therefore also the side DC is equal to the side BC.

And because the side DA is equal to the side AB; [Constr.
and the side AC is common to the two triangles DAC, BAC;
the two sides DA, AC are equal to the two sides BA, AC, each to each;
and the base DC has been shewn to be equal to the base BC;
therefore the angle DAC is equal to the angle BAC. [I. 8.
But DAC is a right angle; [Construction.
therefore also BAC is a right angle. [Axiom 1.

Wherefore, if the square &c. q.e.d.