The Elements of Euclid for the Use of Schools and Colleges/Book II
BOOK II.
DEFINITIONS.
1. Every right-angled parallelogram, or rectangle, is said to be contained by any two of the straight lines which contain one of the right angles.
2. In every parallelogram, any of the parallelograms about a diameter, together with the two complements, is called a Gnomon. 
Thus the parallelogram HG, together with the complements AF,FC, is the gnomon, which is more briefly expressed by the letters AGK, or EHC, which are at the opposite angles of the parallelograms which make the gnomon.
PROPOSITION 1. THEOREM.
If there be two straight lines, one of which is divided into any number of parts, the rectangle contained by the two straight lines is equal to the rectangles contained by the undecided line, and the several parts of the divided line.
Let A and BC be two straight lines; and let BC be divided into any number of parts at the points D, E: the rectangle contained by the straight lines A, BC, shall be equal to the rectangle contained by A, BD, together with that contained by A, DE, and that contained by A, EC.
From the point B draw BF at right angles to BC; [I. 11.
and make BG equal to A; [I. 3.
through G draw GH parallel to BC;, and through D, E, C draw DK, EL, CH, parallel to BG. [I. 31.
Then the rectangle BH is equal to the rectangles BK, DL, EH.
But BH is contained by A, BC, for it is contained by GB, BC, and GB is equal to A. [Construction.
And BK is contained by A, BD, for it is contained by GB, BD, and GB is equal to A;
and DL is contained by A, DE, because DK is equal to BG, which is equal to A; [I. 34.
and in like manner EH is contained by A, EC.
PROPOSITION 2. THEOREM.
If a straight line be divided into any two parts, the rectangles contained by the whole and each of the parts, are together equal to the square on the whole line.
Let the straight line AB be divided into any two parts at the point C: the rectangle contained by AB, BC, together with the rectangle AB, AC, shall be equal to the square on AB.
[Note. To avoid repeating the word contained too frequently, the rectangle contained by two straight lines AB, AC is sometimes simply called the rectangle AB, AC.]
On AB describe the square ADEB; [I.46.
and through C draw CF parallel to AD or BE. [I.31.
Then AE is equal to the rectangles AF, CE.
But AE is the square on AB.
And AF is the rectangle contained by BA, AC, for it is contained by DA, AC, of which DA is equal to BA;
and CE is contained by AB, BC, for BE is equal to AB.
Therefore the rectangle AB, AC, together with the rectangle AB, BC, is equal to the square on AB.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 3. THEOREM.
If a straight line be divided into any two parts, the rectangle contained by the whole and one of the parts, is equal to the rectangle contained by the two parts, together with the square on the aforesaid part.
Let the straight line AB be divided into any two parts at the point C: the rectangle AB, BC shall be equal to the rectangle AC, CB, together with the square on BC.
On BC describe the square CDEB; [I. 46.
produce ED to F, and through A draw AF parallel to CD or BE. [I. 31.
Then the rectangle AE is equal to the rectangles AD, CE.
But AE is the rectangle contained by AB, BC, for it is contained by AB, BE, of which BE is equal to BC;
and AD is contained by AC, CB, for CD is equal to CB;
and CE is the square on BC.
Therefore the rectangle AB, BC is equal to the rectangle AC, CB, together with the square on BC.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 4. THEOREM.
If a straight line be divided into any two parts, the square on the whole line is equal to the squares on the two parts, together with twice the rectangle contained by the two parts.
Let the straight line AB be divided into any two parts at the point C: the square on AB shall be equal to the squares on AC, CB, together with twice the rectangle contained by AC, CB.
On AB describe the square ADEB; [I. 46.
join BD; through C draw CGF parallel to AD or BE, and through G draw HK parallel to AB or DE. [I. 31.
Then, because CF is parallel to AD, and BD falls on them, the exterior angle CGB is equal to the interior and opposite angle ADB; [I. 29.
but the angle ADB is equal to the angle ABD, [I. 5.
because BA is equal to AD, being sides of a square; therefore the angle CGB is equal to the angle CBG; [Ax. 1.
and therefore the side CG is equal to the side CB. [I. 6.
But CB is also equal to GK, and CG to BK; [I. 34.
therefore the figure CGKB is equilateral. It is likewise rectangular. For since CG is parallel to
BK, and CB meets them, the angles KBC, GCB are together equal to two right angles. [I. 29.
But KBC is a right angle. [I. Definition 30.
Therefore GCB is a right angle. [Axiom 3.
And therefore also the angles CGK, GKB opposite to
these are right angles. [I. 34. and Axiom 1.
Therefore CGKB is rectangular ;
and it has been shewn to be equi-
lateral ; therefore it is a square, and
it is on the side CB.
For the same reason HF is also a
square, and it is on the side HG,
which is equal to AC. [I. 34.
Therefore HF, CK are the squares
on AC,CB.
And because the complement AG is equal to the complement GE; [I.43.
and that AG is the rectangle contained by AC, CB, for
CG is equal to CB;
therefore GE is also equal to the rectangle AC, CB. [Ax. 1.
Therefore AG, GE are equal to twice the rectangle AC, CB.
And HF, CK are the squares on AC, CB.
Therefore the four figures HF, CK, AG, GE are equal to
the squares on AC, CB, together with twice the rectangle
AC, CB.
But HF, CK, AG, GE make up the whole figure ADEB,
which is the square on AB.
Therefore the square on AB is equal to the squares on
AC, CB, together with twice the rectangle AC, CB.
Wherefore, if a straight line &c. q.e.d.
Corollary. From the demonstration it is manifest, that parallellograms about the diameter of a square are likewise squares.
PROPOSITION 5. THEOREM.
If a straight line be divided into two equal parts and also into two unequal parts, the rectangle contained by the unequal parts, together with the square on the line between the points of section, is equal to the square on half the line.
Let the straight line AB be divided into two equal parts at the point C, and into two unequal parts at the point D : the rectangle AD,DB, together with the square on CD, shall be equal to the square on CB.
On CB describe the
square CEFB ; [l- 46.
join BE; through D draw
DHG parallel to CE or BF;
through H draw KLM paral-
lel to CB or EF ; and through
A draw AK parallel to CL
or BM. [I. 31.
Then the complement CH is equal to the complement HF, [I. 43.
to each of these add DM therefore the whole CM is equal
to the whole DF. [Axiom 2.
But CM is equal to AL, [I. 36.
because AC is equal to CB. [Hypothesis.
Therefore also AL is equal to DF, [Axiom 1.
To each of these add CH; therefore the whole AH is equal
to DF and CH. [Axiom 2.
But AH is the rectangle contained by AD, DB, for DH is equal to DB ; [II. 4, Corollary.
and DF together with CH is the gnomon CMG ;
therefore the gnomon CMG is equal to the rectangle AD,DB
To each of these add LG, which is equal to the square on
CD. [II. 4, Corollary, and I. 34.
Therefore the gnomon CMG, together with LG, is equal to
the rectangle AD,DB, together with the square on CD. [Ax.2.
But the gnomon CMG and LG make up the whole figure
CEFB, which is the square on CB.
Therefore the rectangle AD,DB, together with the square on CD, is equal to the square on CB.
Wherefore, if a straight line &c. q.e.d.
Prom this proposition it is manifest that the difference of the squares on two unequal straight lines AC, CD, is equal
to the rectangle contained by their sum and difference. PROPOSITION 6. THEOREM.
If a straight line he bisected, and produced to any point, the rectangle contained by the whole line thus produced, and the part of it produced, together with the square on half the line bisected, is equal to the square on the straight line which is made up of the half and the part produced.
Let the straight line AB be bisected at the point C, and produced to the point D : the rectangle AD, DB, together with the square on CB, shall be equal to the square on CD.
On CD describe the
square CEFD ; [I. 46.
join DE through B draw
BHG parallel to CE or
DF; through H draw
KLM parallel to AD or
EF ; and through A draw
AK parallel to CL or DM. [I. 31.
Then, because AC equal to CB, [Hypothesis.
the rectangle AL is equal to the rectangle CH; [I. 36.
but CH is equal to HF; [I. 43.
therefore also AL is equal to HF. [Axiom 1.
To each of these add CM ;
therefore the whole AM is equal to the gnomon CMG. [Ax. 2.
But AM is, the rectangle contained by AD, DB,
for DM is equal to DB. [II. 4, Corollary.
Therefore the rectangle AD, DB is equal to the gnomon
CMG. [Axiom 1.
To each of these add LG, which is equal to the square on
CB. [II. 4, Corollary, and I. 34.
Therefore the rectangle AD, DB, together with the square
on CB, is equal to the gnomon CMG and the figure LG.
But the gnomon CMG and LG make up the whole figure
CEFD, which is the square on CD.
Therefore the rectangle AD,DB, together with the square
on CB, is equal to the square on CD.
PROPOSITION 7. THEOREM.
If a straight line he divided into any two parts, the squares on the whole line, and on one of the parts, are equal to twice the rectangle contained by the whole and that part, together with the square on the other part.
Let the straight line AB be divided into any two parts at the point C: the squares on AB, BC shall be equal to twice the rectangle AB, BC together with the square on AC.
On AB describe the square
ADEB, and construct the figure
as in the preceding propositions.
Then AG is equal to GE ; [1. 43.
to each of these add CK;
therefore the whole AK is equal to
the whole CE ;
therefore AK, CE are double of
AK.
But AK, CE are the gnomon AKF, together with the square CK;
therefore the gnomon AKF, together with the square CK,
is double of AK.
But twice the rectangle AB, BC is double of AK,
for BK is equal to BC. [II. 4, Corollary.
Therefore the gnomon AKF, together with the square CK,
is equal to twice the rectangle AB, BC.
To each of these equals add HF, which is equal to the
square on AG. [II. 4, Corollary, and I. 34.
Therefore the gnomon AKF, together with the squares
GK, HF, is equal to twice the rectangle AB, BC, together
with the square on AC.
But the gnomon AKF together with the squares GK, HF,
make up the whole figure ADEB and GK, which are the squares on AB and BC.
Therefore the squares on AB, BC, are equal to twice the
rectangle AB, BC, together with the square on AC.
PROPOSITION 8. THEOREM.
If a straight line be divided into any two parts, four times the rectangle contained by the whole line and one of the parts, together with the square on the other part, is equal to the square on the straight line which is made up of the whole and that part.
Let the straight line AB be divided into any two parts at the point C: four times the rectangle AB, BC, together with the square on AC shall be equal to the square on the straight line made up of AB and BC together.
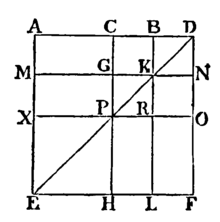
Produce AB to D, so that BD may be equal to CB; [Post. 2. and I. 3.
on AD describe the square AEFD;
and construct two figures such as in the preceding propositions.
Then, because CB is equal to BD,[Construction.
and that CB is equal to GK, and BD to KN,[I. 34.
therefore GK is equal to KN.[Axiom 1.
For the same reason PR is equal to RO.
And because CB is equal to BD, and GK to KN, the rectangle CK is equal to the rectangle BN, and the rectangle GR to the rectangle RN.[I. 36.
But CK is equal to RN, because they are the complements of the parallelogram CO;[I. 43.
therefore also BN is equal to GR.[Axiom 1.
Therefore the four rectangles BN, CK, GR, RN are equal to one another, and so the four are quadruple of one of them CK.
Again, because CB is equal to BD, [Construction.
and that BD is equal to BK, [II. 4, Corollary.
that is to CG, [I. 34.
and that CB is equal to GK, [I. 34.
that is to GP; [II. 4, Corollary.
therefore CG is equal to GP. [Axiom 1.
And because CG is equal to GP, and PR to RO, the rectangle AG is equal to the rectangle MP, and the rectangle PL to the rectangle RF, [I. 36.
But MP is equal to PL, because they are the complements of the parallelogram ML; [I. 43.
therefore also AG is equal to RF. [Axiom 1.
Therefore the four rectangles AG, MP, PL, RF are equal to one another, and so the four are quadruple of one of them AG.
And it was shewn that the four CK, BN, GR and RN are quadruple of CK; therefore the eight rectangles which make up the gnomon AOH are quadruple of AK.
And because AK is the rectangle contained by AB, BC; for BK is equal to BC;
therefore four times the rectangle AB, BC is quadruple of AK.
But the gnomon AOH was shewn to be quadruple of AK,
Therefore four times the rectangle AB, BC is equal to the gnomon AOH. [Axiom 1.
To each of these add XH, which is equal to the square on AC. [II. 4, Corollary, and I. 34.
Therefore four times the rectangle AB, BC, together with the square on AC, is equal to the gnomon AOH and the square XH.
But the gnomon AOH and the square XH make up the figure AEFD, which is the square on AD.
Therefore four times the rectangle AB, BC, together with the square on AC, is equal to the square on AD, that is to the square on the line made of AB and BC together.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 9. THEOREM.
If a straight line he divided into two equals and also into two unequal parts, the squares on the two unequal parts are together double of the square on half the line and of the square on the line between the points of section.
Let the straight line AB be divided into two equal parts at the point C, and into two unequal parts at the point D : the squares on AD, DB shall be together double of the squares on AC, CD.
From the point C draw
CE at right angles to AB [I. 11.
and make it equal to AC or .
CB, [I. 3.
and join EA, EB ; through
D draw DF parallel to CE, and
through F draw FG parallel
to BA ; [I. 31.
and join AF.
Then, because AC is equal to CE, [Construction.
the angle EAC is equal to the angle AEC. [I. 5.
And because the angle ACE is a right angle, [Construction.
the two other angles AEC, EAC are together equal to one
right angle ; [I. 32.
and they are equal to one another ;
therefore each of them is half a right angle.
For the same reason each of the angles CEB, EBC is half
a right angle.
Therefore the whole angle AEB is a right angle.
And because the angle GEF is half a right angle, and the angle EGF a right angle, for it is equal to the interior
and opposite angle ECB ; [I. 29.
therefore the remaining angle EFG is half a right angle.
Therefore the angle GEF is equal to the angle EFG, and
the side EG is equal to the side GF. [I. 6.
therefore the remaining angle BFD is half a right angle.
Therefore the angle at B is equal to the angle BFD and the side DF is equal to the side DB. [I. 6.
And because AC is equal to CE [Construction.
the square on AC is equal to the square on CE;
therefore the squares on AC, CE are double of the square on AC.
But the square on AE is equal to the squares on AC, CE, because the angle ACE is a right angle; [I. 47.
therefore the square on AE is double of the square on AC.
Again, because EG is equal to GF, [Construction.
the square on EG is equal to the square on GF;
therefore the squares on EG, GF are double of the square on GF.
But the square on EF is equal to the squares on EG, GF, because the angle EGF is a right angle; [I. 47.
therefore the square on EF is double of the square on GF. And GF is equal to CD; [I. 34.
therefore the square on EF is double of the square on CD.
But it has been shewn that the square on AE is also double of the square on AC.
Therefore the squares on AE, EF are double of the squares on AC, CD.
But the square on AF is equal to the squares on AE, EF, because the angle AEF is a right angle, [I. 47.
Therefore the square on AF is double of the squares on AC, CD.
But the squares on AD, DF are equal to the square on AF, because the angle ADF is a right angle. [I. 47.
Therefore the squares on AD, DF are double of the squares on AC, CD.
And DF is equal to DB;
therefore the squares on AD, DB are double of the squares on AC, CD.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 10. THEOREM.
If a straight line he bisected, and produced to any point, the square on the whole line thus produced, and the square on the part of it produced, are together double of the square on half the line bisected and of the square on the line made up of the half and the part produced.
Let the straight line AB be bisected at C, and pro- duced to D : the squares on AD, DB shall be together double of the squares on AC, CD.
From the point C draw CE at right angles to AB, [I, 11.
and make it equal to AC
or CB; [1.3.
and join AE,EB ; through
E draw EF parallel to
AB, and through D draw
DF parallel to CE. [1.31
Then because the straight
line EF meets the parallels
EC, FD, the angles CEF, CFD are together equal to two
right angles ; [I. 29.
and therefore the angles BEF, EFD are together less
than two right angles.
Therefore the straight lines EB, FD will meet, if produced,
towards B, D, [Axiom 12.
Let them meet at G, and join AG.
Then because AC is equal to CE, [Construction.
the angle CEA is equal to the angle EAC ; [I. 5.
and the angle ACE is a right angle ; [Construction.
therefore each of the angles CEA, EAC is half a right angle. [I. 32.
For the same reason each of the angles CEB, EBC is half
a right angle.
Therefore the angle AEB is a right angle.
And because the angle EBC is half a right angle,
the angle DBG is also half a right angle, for they are verti-
cally opposite ; [I. 15.
but the angle BDG is a right angle, because it is equal to
the alternate angle DCE ; [I. 29.
and is therefore equal to the angle DBG;
therefore also the side BD is equal to the side DG. [I. 6.
Again, because the angle EGF is half a right angle, and the angle at F a right angle, for it is equal to the opposite angle ECD; [I. 34.
therefore the remaining angle FEG is half a right angle, [I. 32.
and is therefore equal to the angle EGF;
therefore also the side GF is equal to the side FE. [I. 6.
And because EC is equal to CA, the square on EC is equal to the square on CA;
therefore the squares on EC,CA are double of the square on CA.
But the square on AE is equal to the squares on EC, CA. [I. 47.Therefore the square on AE is double of the square on AC.
Again, because GF is equal to FE, the square on GF is equal to the square on FE;
therefore the squares on GF, FE are double of the square on FE.
But the square on EG is equal to the squares on GF, FE. [I. 47.
Therefore the square on EG is double of the square on FE. And FE is equal to CD; [I. 34.
Therefore the square on EG is double of the square on CD.
But it has been shewn that the square on AE is double of the square on AC.
Therefore the squares on AE, EG are double of the squares on AC, CD.
But the square on AG is equal to the squares on AE,EG. [I. 47.
Therefore the square on AG is double of the squares on AC, CD.
But the squares on AD, DG are equal to the square on AG. [I. 47.
Therefore the squares on AD, DG are double of the squares on AC, CD.
And DG equal to DB;
therefore the squares on AD, DB are double of the squares on AC,CD.
Wherefore, if a straight line &c. Q.E.D.
PROPOSITION 11. PROBLEM.
To divide a given straight line into two parts, so that the rectangle contained by the whole and one of the parts may be equal to the square on the other part.
Let AB be the given straight line: it is required to divide it into two parts, so that the rectangle contained by the whole and one of the parts may be equal to the square on the other part.
On AB describe the square
ABDC; [I. 46.
bisect AC at E; [I. 10.
join BE; produce CA to F, and
make EF equal to EB; [I. 3.
and on AF describe the square
AFGH. [1. 46.
AB shall be divided at H so
that the rectangle AB, BH is
equal to the square on AH.
Produce GH to K.
Then, because the straight line
AC is bisected at E, and pro-
duced to F, the rectangle CF, FA, together with the
square on AE, is equal to the square on EF. [II. 6.
But EF is equal to EB. [Construction.
Therefore the rectangle CF, FA, together with the square
on AE, is equal to the square on EB.
But the square on EB is equal to the squares on AE,AB,
because the angle EAB is a right angle. [I. 47.
Therefore the rectangle CF, FA, together with the square
on AE, is equal to the squares on AE, AB.
Take away the square on AE, which is common to both;
therefore the remainder, the rectangle CF, FA, is equal to
the square on AB. [Axiom 3.
But the figure FK is the rectangle contained by CF, FA,
for FG is equal to FA;
and AD is the square on AB;
therefore FK is equal to AD.
Take away the common part AK, and the remainder FH
is equal to the remainder HD. [Axiom 3.
But HD is the rectangle contained by AB, BH, for AB is
equal to BD ;
and FH is the square on AH;
therefore the rectangle AB,BH is equal to the square on AH.
Wherefore the straight line AB is divided at H, so that the rectangle AB, BH is equal to the square on AH. q.e.f.
PROPOSITION 12. THEOREM.
In obtuse-angled triangles, if a perpendicular be drawn from either of the acute angles to the opposite side produced, the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle, by twice the rectangle contained by the side on which, then produced, the perpendicular falls, and the straight line intercepted without the triangle, between the perpendicular and the obtuse angle.
Let ABC be an obtuse-angled triangle, having the obtuse angle ACB, and from the point A let AD be drawn perpendicular to BC produced ; the square on AB shall be greater than the squares on AC, CB, by twice the rectangle BC, CD.
Because the straight line
BD is divided into two parts
it the point C, the square on
BD is equal to the squares on
BC, CD, and twice the rectangle
BC, CD. [II. 4.
To each of these equals add the
quare on DA.
Therefore the squares on BD, DA are equal to the squares on
BC, CD, DA, and twice the rectangle BC, CD. [Axiom 2.
But the square on BA is equal to the squares on BD, DA,
because the angle at D is a right angle ; [I. 47.
and the square on CA is equal to the squares on CD, DA. [1. 47.
therefore the square on BA is equal to the squares on
BC, CA, and twice the rectangle BC, CD ;
that is, the square on BA is greater than the squares on
BC, CA by twice the rectangle BC, CD.
PROPOSITION 13. THEOREM.
In every triangle, the square on the side subtending an acute angle, is less than the squares on the sides containing that angle, by twice the rectangle contained by either of these sides, and the straight line intercepted between the perpendicular let fall on it from the opposite angle, and the acute angle.
Let ABC be any triangle, and the angle at B an acute angle ; and on BC one of the sides containing it, let fall the perpendicular AD from the opposite angle: the square on AC, opposite to the angle B, shall be less than the squares on CB, BA, by twice the rectangle CB, BD.
First, let AD fall within the
triangle ABC.
Then, because the straight line
CB is divided into two parts
at the point D, the squares on
CB, BD are equal to twice the
rectangle contained by CB, BD
and the square on CD. [II. 7.
To each of these equals add the
square on DA.
Therefore the squares on CB, BD, DA are equal to twice
the rectangle CB, BD and the squares on CD, DA. [Ax. 2.
But the square on AB is equal to the squares on BD, DA,
because the angle BDA is a right angle ; [I. 47.
and the square on AC is equal to the squares on CD, DA. [I. 47.
Therefore the squares on CB, BA are equal to the square
on AC and twice the rectangle CB, BD ;
that is, the square on AC alone is less than the squares on
CB, BA by twice the rectangle CB, BD.
Secondly, let AD fall without
the triangle ABC.
Then because the angle at D is
a right angle, [Construction.
the angle ACB is greater than
a right angle ; [I. 1.
and therefore the square on AB is equal to the squares on AC, CB, and twice the rectangle BC, CD. [II. 12.
To each of these equals add the square on BC.
Therefore the squares on AB, BC are equal to the square on AC, and twice the square on BC, and twice the rectangle BC, CD. [Axiom 2.
But because BD is divided into two parts at C, the rectangle DB, BC is equal to the rectangle BC, CD and the square on BC; [II. 3.
and the doubles of these are equal,
that is, twice the rectangle DB, BC is equal to twice the rectangle BC, CD and twice the square on BC.
Therefore the squares on AB, BC are equal to the square on AC, and twice the rectangle DB, BC;
that is, the square on AC alone is less than the squares on AB, BC by twice the rectangle DB, BC.
Lastly, let the side AC be perpendicular to BC.
Then BC is the straight line between the perpendicular and the acute angle at B;
and it is manifest, that the squares on AB, BC are equal to the square on AC, and twice the square on BC. [I. 47 and Ax. 2.
Wherefore, in every triangle &c. q.e.d.
PROPOSITION 14. PROBLEM.
To describe a square that shall he equal to a given rectilineal figure.
Let A be the given rectilineal figure: it is required to describe a square that shall be equal to A.
Describe the rectangular parallelogram BCDE equal to the rectilineal figure A. [1. 45.
Then if the sides of it, BE, ED are equal to one another, it is a square, and what was required is now done.
But if they are not equal, produce one of them BE to F make EF equal to ED, [I. 3. 
and bisect BF at G; [I. 10.
from the centre G, at the distance GB, or GF, describe the semicircle BHF, and produce DE to H.
The square described on EH shall be equal to the given rectilineal figure A.
Join GH. Then, because the straight line BF is divided into two equal parts at the point G, and into two unequal parts at the point E, the rectangle BE, EF, together with the square on GE, is equal to the square on GF. [II. 5.
But GF is equal to GH.
Therefore the rectangle BE, EF, together with the square on GE, is equal to the square on GH.
But the square on GH is equal to the squares on GE, EH;[I.47.
therefore the rectangle BE, EF, together with the square on GE, is equal to the squares on GE, EH.
Take away the square on GE, which is common to both;
therefore the rectangle BE, EF is equal to the square on EH. [Axiom 3.
But the rectangle contained by BE, EF is the parallelogram BD,
because EF is equal to ED. [Construction.
Therefore BD is equal to the square on EH.
But BD is equal to the rectilineal figure A. [Construction.
Therefore the square on EH is equal to the rectilineal figure A.
Wherefore a square has been made equal to the given rectilineal figure A, namely, the square described on EH.q.e.f