CHAPTER II.
FURTHER DISCUSSION UPON THE NATURE OF THE SERIES MENTIONED IN THE LAST CHAPTER.
§ 1. In the course of the last chapter the nature of a particular kind of series, that namely, which must be considered to constitute the basis of the science of Probability, has received a sufficiently general explanation for the preliminary purpose of introduction. One might indeed say more than this; for the characteristics which were there pointed out are really sufficient in themselves to give a fair general idea of the nature of Probability, and of the sort of problems with which it deals. But in the concluding paragraphs an indication was given that the series of this kind, as they actually occur in nature or as the results of more or less artificial production, are seldom or never found to occur in such a simple form as might possibly be expected from what had previously been said; but that they are almost always seen to be associated together in groups after a somewhat complicated fashion. A fuller discussion of this topic must now be undertaken.
We will take for examination an instance of a kind with which the investigations of Quetelet will have served to familiarize some readers. Suppose that we measure the heights of a great many adult men in any town or country. These heights will of course lie between certain extremes in each direction, and if we continue to accumulate our measures it will be found that they tend to lie continuously between these extremes; that is to say, that under those circumstances no intermediate height will be found to be permanently unrepresented in such a collection of measurements. Now suppose these heights to be marshalled in the order of their magnitude. What we always find is something of the following kind;—about the middle point between the extremes, a large number of the results will be found crowded together: a little on each side of this point there will still be an excess, but not to so great an extent; and so on, in some diminishing scale of proportion, until as we get towards the extreme results the numbers thin off and become relatively exceedingly small.
The point to which attention is here directed is not the mere fact that the numbers thus tend to diminish from the middle in each direction, but, as will be more fully explained directly, the law according to which this progressive diminution takes place. The word 'law' is here used in its mathematical sense, to express the formula connecting together the two elements in question, namely, the height itself, and the relative number that are found of that height. We shall have to enquire whether one of these elements is a function of the other, and, if so, what function.
§2. After what was said in the last chapter, it need hardly be insisted upon that the interest and significance of such investigations as these are almost entirely dependent upon the statistics being very extensive. In one or other of Quetelet's works on Social Physics[1] will be found a selection of measurements of almost every element which the physical frame of man can furnish:—his height, his weight, the muscular power of various limbs, the dimensions of almost every part and organ, and so on. Some of the most extensive of these express the heights of 25,000 Federal soldiers from the Army of the Potomac, and the circumferences of the chests of 5738 Scotch militia men taken many years ago. Those who wish to consult a large repertory of such statistics cannot be referred to any better sources than to these and other works by the same author[2].
Interesting and valuable, however, as are Quetelet's statistical investigations (and much of the importance now deservedly attached to such enquiries is, perhaps, owing more to his efforts than to those of any other person), I cannot but feel convinced that there is much in what he has written upon the subject which is erroneous and confusing as regards the foundations of the science of Probability, and the philosophical questions which it involves. These errors are not by any means confined to him, but for various reasons they will be better discussed in the form of a criticism of his explicit or implicit expression of them, than in any more independent way.
§3. In the first place then, he always, or almost always, assumes that there can be but one and the same law of arrangement for the results of our observations, measurements, and so on, in these statistical enquiries. That is, he assumes that whenever we get a group of such magnitudes clustering about a mean, and growing less frequent as they depart from that mean, we shall find that this diminution of frequency takes place according to one invariable law, whatever may be the nature of these magnitudes, and whatever the process by which they may have been obtained.
That such a uniformity as this should prevail amongst many and various classes of phenomena would probably seem surprising in any case. But the full significance of such a fact as this (if indeed it were a fact) only becomes apparent when attention is directed to the profound distinctions in the nature and origin of the phenomena which are thus supposed to be harmonized by being brought under one comprehensive principle. This will be better appreciated if we take a brief glance at some of the principal classes into which the things with which Probability is chiefly concerned may be divided. These are of a three-fold kind.
§4. In the first place there are the various combinations, and runs of luck, afforded by games of chance. Suppose a handful, consisting of ten coins, were tossed up a great many times in succession, and the results were tabulated. What we should obtain would be something of the following kind. In a certain proportion of cases, and these the most numerous of all, we should find that we got five heads and five tails; in a somewhat less proportion of cases we should have, as equally frequent results, four heads six tails, and four tails six heads; and so on in a continually diminishing proportion until at length we came down, in a very small relative number of cases, to nine heads one tail, and nine tails one head; whilst the least frequent results possible would be those which gave all heads or all tails[3]. Here the statistical elements under consideration are, as regards their origin at any rate, optional or brought about by human choice. They would, therefore, be commonly described as being mainly artificial, but their results ultimately altogether a matter of chance.
Again, in the second place, we might take the accurate measurements—i.e. the actual magnitudes themselves,—of a great many natural objects, belonging to the same genus or class; such as the cases, already referred to, of the heights, or other characteristics of the inhabitants of any district. Here human volition or intervention of any kind seem to have little or nothing to do with the matter. It is optional with us to collect the measures, but the things measured are quite outside our control. They would therefore be commonly described as being altogether the production of nature, and it would not be supposed that in strictness chance had anything whatever to do with the matter.
In the third place, the result at which we are aiming may be some fixed magnitude, one and the same in each of our successive attempts, so that if our measurements were rigidly accurate we should merely obtain the same result repeated over and over again. But since all our methods of attaining our aims are practically subject to innumerable imperfections, the results actually obtained will depart more or less, in almost every case, from the real and fixed value which we are trying to secure. They will be sometimes more wide of the mark, sometimes less so, the worse attempts being of course the less frequent. If a man aims at a target he will seldom or never hit it precisely in the centre, but his good shots will be more[4] numerous than his bad ones. Here again, then, we have a series of magnitudes (i.e. the deflections of the shots from the point aimed at) clustering about a mean, but produced in a very different way from those of the last two cases. In this instance the elements would be commonly regarded as only partially the results of human volition, and chance therefore as being only a co-agent in the effects produced. With these must be classed what may be called estimates, as distinguished from measurements. By the latter are generally understood the results of a certain amount of mechanism or manipulation; by the former we may understand those cases in which the magnitude in question is determined by direct observation or introspection. The interest and importance of this class, so far as scientific principles are concerned, dates mainly from the investigations of Fechner. Its chief field is naturally to be found amongst psychological data.
Other classes of things, besides those alluded to above, might readily be given. These however are the classes about which the most extensive statistics are obtainable, or to which the most practical importance and interest are attached. The profound distinctions which separate their origin and character are obvious. If they all really did display precisely the same law of variation it would be a most remarkable fact, pointing doubtless to some deep-seated identity underlying the various ways, apparently so widely distinct, in which they had been brought about. The questions now to be discussed are; Is it the case, with any considerable degree of rigour, that only one law of distribution does really prevail? and, in so far as this is so, how does it come to pass?
§ 5. In support of an affirmative answer to the former of these two questions, several different kinds of proof are, or might be, offered.
(I.) For one plan we may make a direct appeal to experience, by collecting sets of statistics and observing what is their law of distribution. As remarked above, this has been done in a great variety of cases, and in some instances to a very considerable extent, by Quetelet and others. His researches have made it abundantly convincing that many classes of things and processes, differing widely in their nature and origin, do nevertheless appear to conform with a considerable degree of accuracy to one and the same[5] law. At least this is made plain for the more central values, for those that is which are situated most nearly about the mean. With regard to the extreme values there is, on the other hand, some difficulty. For instance in the arrangements of the heights of a number of men, these extremes are rather a stumbling-block; indeed it has been proposed to reject them from both ends of the scale on the plea that they are monstrosities, the fact being that their relative numbers do not seem to be by any means those which theory would assign[6]. Such a plan of rejection is however quite unauthorized, for these dwarfs and giants are born into the world like their more normally sized brethren, and have precisely as much right as any others to be included in the formulæ we draw up.
Besides the instance of the heights of men, other classes of observations of a somewhat similar character have been already referred to as collected and arranged by Quetelet. From the nature of the case, however, there are not many appropriate ones at hand; for when our object is, not to illustrate a law which can be otherwise proved, but to obtain actual direct proof of it, the collection of observations and measurements ought to be made upon such a large scale as to deter any but the most persevering computers from undergoing the requisite labour. Some of the remarks made in the course of the note on the opposite page will serve to illustrate the difficulties which would lie in the way of such a mode of proof.
We are speaking here, it must be understood, only of symmetrical curves: if there is asymmetry, i.e. if the Law of Error is different on different sides of the mean, a comparatively very small number of observations would suffice to detect the fact. But, granted symmetry and rapid decrease of frequency on each side of the mean, we could generally select some one species of the exponential curve which should pretty closely represent our statistics in the neighbourhood of the mean. That is, where the statistics are numerous we could secure agreement; and where we could not secure agreement the statistics would be comparatively so scarce that we should have to continue the observations for a very long time in order to prove the disagreement.
§6. Allowing the various statistics such credit as they deserve, for their extent, appropriateness, accuracy and so on, the general conclusion which will on the whole be drawn by almost every one who takes the trouble to consult them, is that they do, in large part, conform approximately to one type or law, at any rate for all except the extreme values. So much as this must be fully admitted. But that they do not, indeed we may say that they cannot, always do so in the case of the extreme values, will become obvious on a little consideration. In some of the classes of things to which the law is supposed to apply, for example, the successions of heads and tails in the throws of a penny, there is no limit to the magnitude of the fluctuations which may and will occur. Postulate as long a succession of heads or of tails as we please, and if we could only live and toss long enough for it we should succeed in getting it at length. In other cases, including many of the applications of Probability to natural phenomena, there can hardly fail to be such limits. Deviations exceeding a certain range may not be merely improbable, that is of very rare occurrence, but they may often from the nature of the case be actually impossible. And even when they are not actually impossible it may frequently appear on examination that they are only rendered possible by the occasional introduction of agencies which are not supposed to be available in the production of the more ordinary or intermediate values. When, for instance, we are making observations with any kind of instrument, the nature of its construction may put an absolute limit upon the possible amount of error. And even if there be not an absolute limit under all kinds of usage it may nevertheless be the case that there is one under fair and proper usage; it being the case that only when the instrument is designedly or carelessly tampered with will any new causes of divergence be introduced which were not confined within the old limits.
Suppose, for instance, that a man is firing at a mark. His worst shots must be supposed to be brought about by a combination of such causes as were acting, or prepared to act, in every other case; the extreme instance of what we may thus term 'fair usage' being when a number of distinct causes have happened to conspire together so as to tend in the same direction, instead of, as in the other cases, more or less neutralizing one another's work. But the aggregate effect of such causes may well be supposed to be limited. The man will not discharge his shot nearly at right angles to the true line of fire unless some entirely new cause comes in, as by some unusual circumstance having distracted his attention, or by his having had some spasmodic seizure. But influences of this kind were not supposed to have been available before; and even if they were we are taking a bold step in assuming that these occasional great disturbances are subject to the same kind of laws as are the aggregates of innumerable little ones.
We cannot indeed lay much stress upon an example of this last kind, as compared with those in which we can see for certain that there is a fixed limit to the range of error. It is therefore offered rather for illustration than for proof. The enormous, in fact inconceivable magnitude of the numbers expressive of the chance of very rare combinations, such as those in question, has such a bewildering effect upon the mind that one may be sometimes apt to confound the impossible with the higher degrees of the merely mathematically improbable.
§7. At the time the first edition of this essay was composed writers on Statistics were, I think, still for the most part under the influence of Quetelet, and inclined to overvalue his authority on this particular subject: of late however attention has been repeatedly drawn to the necessity of taking account of other laws of arrangement than the binomial or exponential.
Mr Galton, for instance,—to whom every branch of the theory of statistics owes so much,—has insisted[7] that the "assumption which lies at the basis of the well-known law of 'Frequency of Error'. . .is incorrect in many groups of vital and social phenomena.. . .For example, suppose we endeavour to match a tint; Fechner's law, in its approximative and simplest form of sensation = log. stimulus, tells us that a series of tints, in which the quantities of white scattered on a black ground are as 1, 2, 4, 8, 16, 32, &c., will appear to the eye to be separated by equal intervals of tint. Therefore, in matching a grey that contains 8 portions of white, we are just as likely to err by selecting one that has 16 portions as one that has 4 portions. In the first case there would be an error in excess, of 8; in the second there would be an error, in deficiency, of 4. Therefore, an error of the same magnitude in excess or in deficiency is not equally probable." The consequences of this assumption are worked out in a remarkable paper by Dr D. McAlister, to which allusion will have to be made again hereafter. All that concerns us here to point out is that when the results of statistics of this character are arranged graphically we do not get a curve which is symmetrical on both sides of a central axis.
§8. More recently, Mr F. Y. Edgeworth (in a report of a Committee of the British Association appointed to enquire into the variation of the monetary standard) has urged the same considerations in respect of prices of commodities. He gives a number of statistics "drawn from the prices of twelve commodities during the two periods 1782–1820, 1820–1865. The maximum and minimum entry for each series having been noted, it is found that the number of entries above the 'middle point,' half-way between the maximum and minimum[8], is in every instance less than half the total number of entries in the series. In the twenty-four trials there is not a single exception to the rule, and in very few cases even an approach to an exception. We may presume then that the curves are of the lop-sided character indicated by the accompanying diagram." The same facts are also ascertained in respect to place variations as distinguished from time variations. To these may be added some statistics of my own, referring to the heights of the barometer taken at the same hour on more than 4000 successive days (v. Nature, Sept. 2, 1887). So far as these go they show a marked asymmetry of arrangement.
In fact it appears to me that this want of symmetry ought to be looked for in all cases in which the phenomena under measurement are of a 'one-sided' character; in the sense that they are measured on one side only of a certain fixed point from which their possibility is supposed to start. For not only is it impossible for them to fall below this point: long before they reach it the influence of its proximity is felt in enhancing the difficulty and importance of the same amount of absolute difference.
Look at a table of statures, for instance, with a mean value of 69 inches. A diminution of three feet (were this possible) is much more influential,—counts for much more, in every sense of the term,—than an addition of the same amount; for the former does not double the mean, while the latter more than halves it. Revert to an illustration. If a vast number of petty influencing circumstances of the kind already described were to act upon a swinging pendulum we should expect the deflections in each direction to display symmetry; but if they were to act upon a spring we should not expect such a result. Any phenomena of which the latter is the more appropriate illustration can hardly be expected to range themselves with symmetry about a mean[9].
§9 (II.). The last remarks will suggest another kind of proof which might be offered to establish the invariable nature of the law of error. It is of a direct deductive kind, not appealing immediately to statistics, but involving an enquiry into the actual or assumed nature of the causes by which the events are brought about. Imagine that the event under consideration is brought to pass, in the first place, by some fixed cause, or group of fixed causes. If this comprised all the influencing circumstances the event would invariably happen in precisely the same way: there would be no errors or deflections whatever to be taken account of. But now suppose that there were also an enormous number of very small causes which tended to produce deflections; that these causes acted in entire independence of one another; and that each of the lot told as often, in the long run, in one direction as in the opposite. It is easy[10] to see, in a general way, what would follow from these assumptions. In a very few cases nearly all the causes would tell in the same direction; in other words, in a very few cases the deflection would be extreme. In a greater number of cases, however, it would only be the most part of them that would tell in one direction, whilst a few did what they could to counteract the rest; the result being a comparatively larger number of somewhat smaller deflections. So on, in increasing numbers, till we approach the middle point. Here we shall have a very large number of very small deflections: the cases in which the opposed influences just succeed in balancing one another, so that no error whatever is produced, being, though actually infrequent, relatively the most frequent of all.
Now if all deflections from a mean were brought about in the way just indicated (an indication which must suffice for the present) we should always have one and the same law of arrangement of frequency for these deflections or errors, viz. the exponential[11] law mentioned in §5.
§10. It may be readily admitted from what we know about the production of events that something resembling these assumptions, and therefore something resembling the consequences which follow from them, is really secured in a very great number of cases. But although this may prevail approximately, it is in the highest degree improbable that it could ever be secured, even artificially, with anything approaching to rigid accuracy. For one thing, the causes of deflection will seldom or never be really independent of one another. Some of them will generally be of a kind such that the supposition that several are swaying in one direction, may affect the capacity of each to produce that full effect which it would have been capable of if it had been left to do its work alone. In the common example, for instance, of firing at a mark, so long as we consider the case of the tolerably good shots the effect of the wind (one of the causes of error) will be approximately the same whatever may be the precise direction of the bullet. But when a shot is considerably wide of the mark the wind can no longer be regarded as acting at right angles to the line of flight, and its effect in consequence will not be precisely the same as before. In other words, the causes here are not strictly independent, as they were assumed to be; and consequently the results to be attributed to each are not absolutely uninfluenced by those of the others. Doubtless the effect is trifling here, but I apprehend that if we were carefully to scrutinize the modes in which the several elements of the total cause conspire together, we should find that the assumption of absolute independence was hazardous, not to say unwarrantable, in a very great number of cases. These brief remarks upon the process by which the deflections are brought about must suffice for the present purpose, as the subject will receive a fuller investigation in the course of the next chapter.
According, therefore, to the best consideration which can at the present stage be afforded to this subject, we may draw a similar conclusion from this deductive line of argument as from the direct appeal to statistics. The same general result seems to be established; namely, that approximately, with sufficient accuracy for all practical purposes, we may say that an examination of the causes by which the deflections are generally brought about shows that they are mostly of such a character as would result in giving us the commonly accepted 'Law of Error' as it is termed[12]. The two lines of enquiry, therefore, within the limits assigned, afford each other a decided mutual confirmation.
§11 (III.). There still remains a third, indirect and mathematical line of proof, which might be offered to establish the conclusion that the Law of Error is always one and the same. It may be maintained that the recognized and universal employment of one and the same method, that known to mathematicians and astronomers as the Method of Least Squares, in all manner of different cases with very satisfactory results, is compatible only with the supposition that the errors to which that method is applied must be grouped (illegible text) to one invariable law. If all 'laws of error' were not of one and the same type, that is, if the relative frequency of large and small divergences (such as we have been speaking of) were not arranged according to one pattern, how could one method or rule equally suit them all?
In order to preserve a continuity of treatment, some notice must be taken of this enquiry here, though, as in the case of the last argument, any thorough discussion of the subject is impossible at the present stage. For one thing, it would involve too much employment of mathematics, or at any rate of mathematical conceptions, to be suitable for the general plan of this treatise: I have (illegible text) devoted a special chapter to the consideration of it.
The main reason, however, against discussing this argument here, is, that to do so would involve the anticipation of a totally different side of the science of Probability from that hitherto treated of. This must be especially insisted upon, as the neglect of it involves much confusion and some error. During these earlier chapters we have been entirely occupied with laying what may be called the physical foundations of Probability. We have done nothing else than establish, in one way or another, the existence of certain groups or arrangements of things which are found to present themselves in nature; we have endeavoured to explain how they come to pass, and we have illustrated their principal characteristics. But these are merely the foundations of Inference, we have not yet said a word upon the logical processes which are to be erected upon these foundations. We have not therefore entered yet upon the logic of chance.
§ 12. Now the way in which the Method of Least Squares is sometimes spoken of tends to conceal the magnitude of this distinction. Writers have regarded it as synonymous with the Law of Error, whereas the fact is that the two are not only totally distinct things but that they have scarcely even any necessary connection with each other. The Law of Error is the statement of a physical fact; it simply assigns, with more or less of accuracy, the relative frequency with which errors or deviations of any kind are found in practice to present themselves. It belongs therefore to what may be termed the physical foundations of the science. The Method of Least Squares, on the other hand, is not a law at all in the scientific sense of the term. It is simply a rule or direction informing us how we may best proceed to treat any group of these errors which may be set before us, so as to extract the true result at which they have been aiming. Clearly therefore it belongs to the inferential or logical part of the subject.
It cannot indeed be denied that the methods we employ must have some connection with the arrangement of the facts to which they are applied; but the two things are none the less distinct in their nature, and in this case the connection does not seem at all a necessary one, but at most one of propriety and convenience. The Method of Least Squares is usually applied, no doubt, to the most familiar and common form of the Law of Error, namely the exponential form with which we have been recently occupied. But other forms of laws of error may exist, and, if they did, the method in question might equally well be applied to them. I am not asserting that it would necessarily be the best method in every case, but it would be a possible one; indeed we may go further and say, as will be shown in a future chapter, that it would be a good method in almost every case. But its particular merits or demerits do not interfere with its possible employment in every case in which we may choose to resort to it. It will be seen therefore, even from the few remarks that can be made upon the subject here, that the fact that one and the same method is very commonly employed with satisfactory results affords little or no proof that the errors to which it is applied must be arranged according to one fixed law.
§ 13. So much then for the attempt to prove the prevalence, in all cases, of this particular law of divergence. The next point in Quetelet's treatment of the subject which deserves attention as erroneous or confusing, is the doctrine maintained by him and others as to the existence of what he terms a type in the groups of things in question. This is a not unnatural consequence from some of the data and conclusions of the last few paragraphs. Refer back to two of the three classes of things already mentioned in § 4. If it really were the case that in arranging in order a series of incorrect observations or attempts of our own, and a collection of natural objects belonging to some one and the same species or class, we found that the law of their divergence was in each case identical in the long run, we should be naturally disposed to apply the same expression 'Law of Error' to both instances alike, though in strictness it could only be appropriate to the former. When we perform an operation ourselves with a clear consciousness of what we are aiming at, we may quite correctly speak of every deviation from this as being an error; but when Nature presents us with a group of objects of any kind, it is using a rather bold metaphor to speak in this case also of a law of error, as if she had been aiming at something all the time, and had like the rest of us missed her mark more or less in almost every instance[13].
Suppose we make a long succession of attempts to measure accurately the precise height of a man, we should from one cause or another seldom or never succeed in doing so with absolute accuracy. But we have no right to assume that these imperfect measurements of ours would be found so to deviate according to one particular law of error as to present the precise counterpart of a series of actual heights of different men, supposing that these latter were assigned with absolute precision. What might be the actual law of error in a series of direct measurements of any given magnitude could hardly be asserted beforehand, and probably the attempt to determine it by experience has not been made sufficiently often to enable us to ascertain it; but upon general grounds it seems by no means certain that it would follow the so-called exponential law. Be this however as it may, it is rather a licence of language to talk as if nature had been at work in the same way as one of us; aiming (ineffectually for the most part) at a given result, that is at producing a man endowed with a certain stature, proportions, and so on, who might therefore be regarded as the typical man.
§ 14. Stated as above, namely, that there is a fixed invariable human type to which all individual specimens of humanity may be regarded as having been meant to attain, but from which they have deviated in one direction or another, according to a law of deviation capable of à priori determination, the doctrine is little else than absurd. But if we look somewhat closer at the facts of the case, and the probable explanation of these facts, we may see our way to an important truth. The facts, on the authority of Quetelet's statistics (the great interest and value of which must be frankly admitted), are very briefly as follows: if we take any element of our physical frame which admits of accurate measurement, say the height, and determine this measure in a great number of different individuals belonging to any tolerably homogeneous class of people, we shall find that these heights do admit of an orderly arrangement about a mean, after the fashion which has been already repeatedly mentioned. What is meant by a homogeneous class? is a pertinent and significant enquiry, but applying this condition to any simple cases its meaning is readily stated. It implies that the mean in question will be different according to the nationality of the persons under measurement. According to Quetelet[14], in the case of Englishmen the mean is about ft. 9 in.; for Belgians about 5 ft. 7 in.; for the French about 5 ft. 4 in. It need hardly be added that these measures are those of adult males.
§ 15. It may fairly be asked here what would have been the consequence, had we, instead of keeping the English and the French apart, mixed the results of our measurements of them all together? The question is an important one, as it will oblige us to understand more clearly what we mean by homogeneous classes. The answer that would usually be given to it, though substantially correct, is somewhat too decisive and summary. It would be said that we are here mixing distinctly heterogeneous elements, and that in consequence the resultant law of error will be by no means of the simple character previously exhibited. So far as such an answer is to be admitted its grounds are easy to appreciate. In accordance with the usual law of error the divergences from the mean grow continuously less numerous as they increase in amount. Now, if we mix up the French and English heights, what will follow? Beginning from the English mean of 5 feet 9 inches, the heights will at first follow almost entirely the law determined by these English conditions, for at this point the English data are very numerous, and the French by comparison very few. But, as we begin to approach the French mean, the numbers will cease to show that continual diminution which they should show, (illegible text) to the English scale of arrangement, for here the French data are in turn very numerous, and the English by comparison few. The result of such a combination of heterogeneous elements is illustrated by the figure annexed, of course in a very exaggerated form.

§ 16. In the above case the nature of the heterogeneity, and the reasons why the statistics should be so collected and arranged as to avoid it, seemed tolerably obvious. It will be seen still more plainly if we take a parallel case drawn from artificial proceedings. Suppose that after a man had fired a few thousand shots at a certain spot, say a wafer fixed somewhere on a wall, the position of the spot at which he aims were shifted, and he fired a few thousand more shots at the wafer in its new position. Now let us collect and arrange all the shots of both series in the order of their departure from either of the centres, say the new one. Here we should really be mingling together two discordant sets of elements, either of which, if kept apart from the other, would have been of a simple and homogeneous character. We should find, in consequence, that the resultant law of error betrayed its composite or heterogeneous origin by a glaring departure from the customary form, somewhat after the fashion indicated in the above diagram.
The instance of the English and French heights resembles the one just given, but falls far short of it in the stringency with which the requisite conditions are secured. The fact is we have not here got the most suitable requirements, viz. a group consisting of a few fixed causes supplemented by innumerable little disturbing influences, What we call a nation is really a highly artificial body, the members of
- ↑ Essai de Physique Sociale, 1869. Anthropométrie, 1870.
- ↑ As regards later statistics on the same subject the reader can refer to the Reports of the Anthropometrical Committee of the British Association (1879, 1880, 1881, 1883;—especially this last). These reports seem to me to represent a great advance on the results obtained by Quetelet, and fully to justify the claim of the Secretary (Mr C. Roberts) that their statistics are "unique in range and numbers". They embrace not merely military recruits—like most of the previous table—but almost every class and age, and both sexes. Moreover they refer not only to stature but to a number of other physical characteristics.
- ↑ As every mathematician knows, the relative numbers of each of these possible throws are given by the successive terms of the expansion of (1 + 1)10, viz. 1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1.
- ↑ That is they will be more densely aggregated. If a space the size of the bull's-eye be examined in each successive circle, the number of shot marks which it contains will be successively less. The actual number of shots which strike the bull's-eye will not be the greatest, since it covers so much less surface than any of the other circles.
- ↑ Commonly called the exponential law; its equation being of the form The curve corresponding to it cuts the axis of at right angles (expressing the fact that near the mean there are a large number of values approximately equal; after a time it begins to slope away rapidly towards the axis of ; (expressing the fact that the results soon begin to grow less common as we recede from the mean); and the axis of is an asymptote in both directions (expressing the fact that no magnitude, however remote from the mean, is strictly impossible; that is, every deviation, however excessive, will have to be encountered at length within the range of a sufficiently long experience). The curve is obviously symmetrical, expressing the fact that equal deviations from the mean, in excess and in defect, tend to occur equally often in the long run.
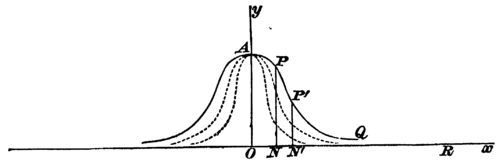
Illustration from Logic of Chance A rough graphic representation of the curve is given above. For the benefit of those unfamiliar with mathematics one or two brief remarks may be here appended concerning some of its properties. (1) It must not be supposed that all specimens of the curve are similar to one another. The dotted lines are equally specimens of it. In fact, by varying the essentially arbitrary units in which and are respectively estimated, we may make the portion towards the vortex of the curve as obtuse or as acute as we please. This consideration is of importance; for it reminds us that, by varying one of these arbitrary units, we could get an 'exponential curve' which should tolerably closely resemble any symmetrical curve of error, provided that this latter recognized and was founded upon the assumption that extreme divergences were excessively rare. Hence it would be difficult, by mere observation, to prove that the law of error in any given case was not exponential; unless the statistics were very extensive, or the actual results departed considerably from the exponential form. (2) It is quite impossible by any graphic representation to give an adequate idea of the excessive rapidity with which the curve after a time approaches the axis of . At the point , on our scale, the curve would approach within the fifteen-thousandth part of an inch from the axis of , a distance which only a very good microscope could detect. Whereas in the hyperbola, e.g. the rate of approach of the curve to its asymptote is continually decreasing, it is here just the reverse; this rate is continually increasing. Hence the two, viz. the curve and the axis of , appear to the eye, after a very short time, to merge into one another.
- ↑ As by Quetelet: noted, amongst others, by Herschel, Essays, page 409.
- ↑ Proc. R. Soc. Oct. 21, 1879.
- ↑ We are here considering, remember, the case of a finite amount of statistics; so that there are actual limits at each end.
- ↑ It must be admitted that experience has not yet (I believe) shown this symmetry in respect of heights.
- ↑ The above reasoning will probably be accepted as valid at this stage of enquiry. But in strictness, assumptions are made here, which however justifiable they may be in themselves, involve somewhat of an anticipation. They demand, and in a future chapter will receive, closer scrutiny and criticism.
- ↑ A definite numerical example of this kind of concentration of frequency about the mean was given in the note to §4. It was of a binomial form, consisting of the successive terms of the expansion of . Now it may be shown (Quetelet, Letters, p. 263; Liagre, Calcul des probabilités, §34) that the expansion of such a binomial, as becomes indefinitely great, approaches as its limit the exponential form; that is, if we take a number of equidistant ordinates proportional respectively to 1, , &c., and connect their vertices, the figure we obtain approximately represents some form of the curve , and tends to become identical with it, as is increased without limit. In other words, if we suppose the errors to be produced by a limited number of finite, equal and independent causes, we have an approximation to the exponential Law of Error, which merges into identity as the causes are increased in number and diminished in magnitude without limit. Jevons has given (Principles of Science, p. 381) a diagram drawn to scale, to show how rapid this approximation is. One point must be carefully remembered here, as it is frequently overlooked (by Quetelet, for instance). The coefficients of a binomial of two equal terms—as , in the preceding paragraph—are symmetrical in their arrangement from the first, and very speedily become indistinguishable in (graphical) outline from the final exponential form. But if, on the other hand, we were to consider the successive terms of such a binomial as (which are proportional to the relative chances of 0, 1, 2, 3, . . . failures in ventures, of an event which has one chance in its favour to four against it) we should have an unsymmetrical succession. If however we suppose to increase without limit, as in the former supposition, the unsymmetry gradually disappears and we tend towards precisely the same exponential form as if we had begun with two equal terms. The only difference is that the position of the vertex of the curve is no longer in the centre: in other words, the likeliest term or event is not an equal number of successes and failures but successes and failures in the ratio of 1 to 4.
- ↑ 'Law of Error' is the usual technical term for what has been elsewhere spoken of above as a Law of Divergence from a mean. It is in strictness only appropriate in the case of one, namely the third, of the three classes of phenomena mentioned in §4, but by a convenient generalization it is equally applied to the other two; so that we term the amount of the divergence from the mean an 'error' in every case, however it may have been brought about.
- ↑ This however seems to be the purport, either by direct assertion or by implication, of two elaborate works by Quetelet, viz. his Physique Sociale, and his Anthropométrie.
- ↑ He scarcely, however, professes to give these as an accurate measure of the mean height, nor does he always give precisely the same measure. Practically, none but soldiers being measured in any great numbers, the English stature did not afford accurate data on any large scale. The statistics given a few pages further on are probably far more trustworthy.








