ABERRATION (Lat. ab, from or away, errare, to wander), a deviation or wandering, especially used in the figurative sense: as in ethics, a deviation from the truth; in pathology, a mental derangement; in zoology and botany, abnormal development or structure. In optics, the word has two special applications: (1) Aberration of Light, and (2) Aberration in Optical Systems. These subjects receive treatment below.
I. Aberration of Light
This astronomical phenomenon may be defined as an apparent motion of the heavenly bodies; the stars describing annually orbits more or less elliptical, according to the latitude of the star; consequently at any moment the star appears to be displaced from its true position. This apparent motion is due to the finite velocity of light, and the progressive motion of the observer with the earth, as it performs its yearly course about the sun. It may be familiarized by the following illustrations. Alexis Claude Clairaut gave this figure: Imagine rain to be falling vertically, and a person carrying a thin perpendicular tube to be standing on the ground. If the bearer be stationary, rain-drops will traverse the tube without touching its sides; if, however, the person be walking, the tube must be inclined at an angle varying as his velocity in order that the rain may traverse the tube centrally. (J. J. L. de Lalande gave the illustration of a roofed carriage with an open front: if the carriage be stationary, no rain enters; if, however, it be moving, rain enters at the front. The “umbrella” analogy is possibly the best known figure.

Fig. 1.When stationary, the most efficient position in which to hold an umbrella is obviously vertical; when walking, the umbrella must be held more and more inclined from the vertical as the walker quickens his pace. Another familiar figure, pointed out by P. L. M. de Maupertuis, is that a sportsman, when aiming at a bird on the wing, sights his gun some distance ahead of the bird, the distance being proportional to the velocity of the bird. The mechanical idea, named the parallelogram of velocities, permits a ready and easy graphical representation of these facts. Reverting to the analogy of Clairaut, let AB (fig. 1) represent the velocity of the rain, and AC the relative velocity of the person bearing the tube. The diagonal AD of the parallelogram, of which AB and AC are adjacent sides, will represent, both in direction and magnitude, the motion of the rain as apparent to the observer. Hence for the rain to centrally traverse the tube, this must be inclined at an angle BAD to the vertical; this angle is conveniently termed the aberration: due to these two motions. The umbrella analogy is similarly explained; the most efficient position being when the stick points along the resultant AD.
The discovery of the aberration of light in 1725, due to James Bradley, is one of the most important in the whole domain of astronomy. That it was unexpected there can be no doubt; and it was only by extraordinary perseverance and perspicuity that Bradley was able to explain it in 1727. Its origin is seated in attempts made to free from doubt the prevailing discordances as to whether the stars possessed appreciable parallaxes. The Copernican theory of the solar system—that the earth revolved annually about the sun—had received confirmation by the observations of Galileo and Tycho Brahe, and the mathematical investigations of Kepler and Newton. As early as 1573, Thomas Digges had suggested that this theory should necessitate a parallactic shifting of the stars, and, consequently, if such stellar parallaxes existed, then the Copernican theory would receive additional confirmation. Many observers claimed to have determined such parallaxes, but Tycho Brahe and G. B. Riccioli concluded that they existed only in the minds of the observers, and were due to instrumental and personal errors. In 1680 Jean Picard, in his Voyage d’Uranibourg, stated, as a result of ten years’ observations, that Polaris, or the Pole Star, exhibited variations in its position amounting to 40″ annually; some astronomers endeavoured to explain this by parallax, but these attempts were futile, for the motion was at variance with that which parallax would occasion. J. Flamsteed, from measurements made in 1689 and succeeding years with his mural quadrant, similarly concluded that the declination of the Pole Star was 40″ less in July than in September. R. Hooke, in 1674, published his observations of γ Draconis, a star of the second magnitude which passes practically overhead in the latitude of London, and whose observations are therefore singularly free from the complex corrections due to astronomical refraction, and concluded that this star was 23″ more northerly in July than in October.
When James Bradley and Samuel Molyneux entered this sphere of astronomical research in 1725, there consequently prevailed much uncertainty as to whether stellar parallaxes had been observed or not; and it was with the intention of definitely answering this question that these astronomers erected a large telescope at the house of the latter at Kew. They determined to reinvestigate the motion of γ Draconis; the telescope, constructed by George Graham (1675–1751), a celebrated instrument-maker, was affixed to a vertical chimney-stack, in such manner as to permit a small oscillation of the eyepiece, the amount of which, i.e. the deviation from the vertical, was regulated and measured by the introduction of a screw and a plumb-line. The instrument was set up in November 1725, and observations on γ Draconis were made on the 3rd, 5th, 11th, and 12th of December. There was apparently no shifting of the star, which was therefore thought to be at its most southerly point. On the 17th of December, however, Bradley observed that the star was moving southwards, a motion further shown by observations on the 20th. These results were unexpected, and, in fact, inexplicable by existing theories; and an examination of the telescope showed that the observed anomalies were not due to instrumental errors. The observations were continued, and the star was seen to continue its southerly course until March, when it took up a position some 20″ more southerly than its December position. After March it began to pass northwards, a motion quite apparent by the middle of April; in June it passed at the same distance from the zenith as it did in December; and in September it passed through its most northerly position, the extreme range from north to south, i.e. the angle between the March and September positions, being 40″.
This motion is evidently not due to parallax, for, in this case, the maximum range should be between the June and December positions; neither was it due to observational errors. Bradley and Molyneux discussed several hypotheses in the hope of fixing the solution. One hypothesis was: while γ Draconis was stationary, the plumb-line, from which the angular measurements were made, varied; this would follow if the axis of the earth varied. The oscillation of the earth’s axis may arise in two distinct ways; distinguished as “nutation of the axis” and “variation of latitude.” Nutation, the only form of oscillation imagined by Bradley, postulates that while the earth’s axis is fixed with respect to the earth, i.e. the north and south poles occupy permanent geographical positions, yet the axis is not directed towards a fixed point in the heavens; variation of latitude, however, is associated with the shifting of the axis within the earth, i.e. the geographical position of the north pole varies.
Nutation of the axis would determine a similar apparent motion for all stars: thus, all stars having the same polar distance as γ Draconis should exhibit the same apparent motion after or before this star by a constant interval. Many stars satisfy the condition of equality of polar distance with that of γ Draconis, but few were bright enough to be observed in Molyneux’s telescope. One such star, however, with a right ascension nearly equal to that of γ Draconis, but in the opposite sense, was selected and kept under observation. This star was seen to possess an apparent motion similar to that which would be a consequence of the nutation of the earth’s axis; but since its declination varied only one half as much as in the case of γ Draconis, it was obvious that nutation did not supply the requisite solution. The question as to whether the motion was due to an irregular distribution of the earth’s atmosphere, thus involving abnormal variations in the refractive index, was also investigated; here, again, negative results were obtained.
Bradley had already perceived, in the case of the two stars previously scrutinized, that the apparent difference of declination from the maximum positions was nearly proportional to the sun’s distance from the equinoctial points; and he realized the necessity for more observations before any generalization could be attempted. For this purpose he repaired to the Rectory, Wanstead, then the residence of Mrs Pound, the widow of his uncle James Pound, with whom he had made many observations of the heavenly bodies. Here he had set up, on the 19th of August 1727, a more convenient telescope than that at Kew, its range extending over 614° on each side of the zenith, thus covering a far larger area of the sky. Two hundred stars in the British Catalogue of Flamsteed traversed its field of view; and, of these, about fifty were kept under close observation. His conclusions may be thus summarized: (1) only stars near the solstitial colure had their maximum north and south positions when the sun was near the equinoxes, (2) each star was at its maximum positions when it passed the zenith at six o’clock morning and evening (this he afterwards showed to be inaccurate, and found the greatest change in declination to be proportional to the latitude of the star), (3) the apparent motions of all stars at about the same time was in the same direction.
 Fig. 2. |
Let S (fig. 2) be a star and the observer be carried along the line AB; let SB be perpendicular to AB. If the observer be stationary at B, the star will appear in the direction BS; if, however, he traverses the distance BA in the same time as light passes from the star to his eye, the star will appear in the direction AS. Since, however, the observer is not conscious of his own translatory motion with the earth in its orbit, the star appears to have a displacement which is at all times parallel to the motion of the observer. To generalize this, let S (fig. 3) be the sun, ABCD the earth’s orbit, and s the true position of a star. When the earth is at A, in consequence of aberration, the star is displaced to a point a, its displacement sa being parallel to the earth’s motion at A; when the earth is at B, the star appears at b; and so on throughout an orbital revolution of the earth. Every star, therefore, describes an apparent orbit, which, if the line joining the sun and the star be perpendicular to the plane ABCD, will be exactly similar to that of the earth, i.e. almost a circle. As the star decreases in latitude, this circle will be viewed more and more obliquely, becoming a flatter and flatter ellipse until, with zero latitude, it degenerates into a straight line (fig. 4).
 Fig. 3. |
 Fig. 4. |
Assured that his explanation was true, Bradley corrected his observations for aberration, but he found that there still remained a residuum which was evidently not a parallax, for it did not exhibit an annual cycle. He reverted to his early idea of a nutation of the earth’s axis, and was rewarded by the discovery that the earth did possess such an oscillation (see Astronomy). Bradley recognized the fact that the experimental determination of the aberration constant gave the ratio of the velocities of light and of the earth; hence, if the velocity of the earth be known, the velocity of light is determined. In recent years much attention has been given to the nature of the propagation of light from the heavenly bodies to the earth, the argument generally being centred about the relative effect of the motion of the aether on the velocity of light. This subject is discussed in the articles Aether and Light.
References.—A detailed account of Bradley’s work is given in S. Rigaud, Memoirs of Bradley (1832), and in Charles Hutton, Mathematical and Philosophical Dictionary (1795); a particularly clear and lucid account is given in H. H. Turner, Astronomical Discovery (1904). The subject receives treatment in all astronomical works.
II. Aberration in Optical Systems
Aberration in optical systems, i.e. in lenses or mirrors or a series of them, may be defined as the non-concurrence of rays from the points of an object after transmission through the system; it happens generally that an image formed by such a system is irregular, and consequently the correction of optical systems for aberration is of fundamental importance to the instrument-maker. Reference should he made to the articles Reflexion, Refraction and Caustic for the general characters of reflected and refracted rays (the article Lens considers in detail the properties of this instrument, and should also be consulted); in this article will be discussed the nature, varieties and modes of aberrations mainly from the practical point of view, i.e. that of the optical-instrument maker.
Aberrations may be divided in two classes: chromatic (Gr. χρῶμα, colour) aberrations, caused by the composite nature of the light generally applied (e.g. white light), which is dispersed by refraction, and monochromatic (Gr. μóνος, one) aberrations produced without dispersion. Consequently the monochromatic class includes the aberrations at reflecting surfaces of any coloured light, and at refracting surfaces of monochromatic or light of single wave length.
(a) Monochromatic Aberration.
The elementary theory of optical systems leads to the theorem; Rays of light proceeding from any “object point,” unite in an “image point”; and therefore an “object space” is reproduced in an “image space.” The introduction of simple auxiliary terms, due to C. F. Gauss (Dioptrische Untersuchungen, Göttingen, 1841), named the focal lengths and focal planes, permits the determination of the image of any object for any system (see Lens). The Gaussian theory, however, is only true so long as the angles made by all rays with the optical axis (the symmetrical axis of the system) are infinitely small, i.e. with infinitesimal objects, images and lenses; in practice these conditions are not realized, and the images projected by uncorrected systems are, in general, ill defined and often completely blurred, if the aperture or field of view exceeds certain limits. The investigations of James Clerk Maxwell (Phil.Mag., 1856; Quart. Journ. Math., 1858, and Ernst Abbe[1]) showed that the properties of these reproductions, i.e. the relative position and magnitude of the images, are not special properties of optical systems, but necessary consequences of the supposition (in Abbe) of the reproduction of all points of a space in image points (Maxwell assumes a less general hypothesis), and are independent of the manner in which the reproduction is effected. These authors proved, however, that no optical system can justify these suppositions, since they are contradictory to the fundamental laws of reflexion and refraction. Consequently the Gaussian theory only supplies a convenient method of approximating to reality; and no constructor would attempt to realize this unattainable ideal. All that at present can be attempted is, to reproduce a single plane in another plane; but even this has not been altogether satisfactorily accomplished, aberrations always occur, and it is improbable that these will ever be entirely corrected.
This, and related general questions, have been treated—besides the above–mentioned authors—by M. Thiesen (Berlin. Akad. Sitzber., 1890, xxxv. 799; Berlin. Phys. Ges. Verh., 1892) and H. Bruns (Leipzig. Math. Phys. Ber., 1895, xxi. 325) by means of Sir W. R. Hamilton’s “characteristic function” (Irish Acad. Trans., “Theory of Systems of Rays,” 1828, et seq.). Reference may also be made to the treatise of Czapski-Eppenstein, pp. 155-161.
A review of the simplest cases of aberration will now be given. (1) Aberration of axial points (Spherical aberration in the restricted sense). If S (fig.5) be any optical system, rays proceeding from an axis point O under an angle u1 will unite in the axis point O′1; and those under an angle u2 in the axis point O′2. If there be refraction at a collective spherical surface, or through a thin positive lens, O′2 will lie in front of O′1 so long as the angle u2 is greater than u1 (“under correction”); and conversely with a dispersive surface or lenses (“over correction”). The caustic, in the first case, resembles the sign > (greater than); in the second < (less than). If the angle u1 be very small, O′1 is the Gaussian image; and O′1 O′2 is termed the “longitudinal aberration,” and O′1R the “lateral aberration” of the pencils with aperture u2. If the pencil with the angle u2 be that of the maximum aberration of all the pencils transmitted, then in a plane perpendicular to the axis at O′1 there is a circular “disk of confusion” of radius O′1R, and in a parallel plane at O′2 another one of radius O′2R2; between these two is situated the “disk of least confusion.”
The largest opening of the pencils, which take part in the reproduction of O, i.e. the angle u, is generally determined by the margin of one of the lenses or by a hole in a thin plate placed between, before, or behind the lenses of the system. This hole is termed the “stop” or “diaphragm”; Abbe used the term “aperture stop” for both the hole and the limiting margin of the lens. The component S1 of the system, situated between the aperture stop and the object O, projects an image of the diaphragm, termed by Abbe the “entrance pupil”; the “exit pupil” is the image formed by the component S2, which is placed behind the aperture stop. All rays which issue from O and pass through the aperture stop also pass through the entrance and exit pupils, since these are images of the aperture stop. Since the maximum aperture of the pencils issuing from O is the angle u subtended by the entrance pupil at this point, the magnitude of the aberration will be determined by the position and diameter of the entrance pupil. If the system be entirely behind the aperture stop, then this is itself the entrance pupil (“front stop”); if entirely in front, it is the exit pupil (“back stop”).
If the object point be infinitely distant, all rays received by the first member of the system are parallel, and their intersections, after traversing the system, vary according to their “perpendicular height of incidence,” i.e. their distance from the axis. This distance replaces the angle u in the preceding considerations; and the aperture, i.e. the radius of the entrance pupil, is its maximum value.
 Fig. 5. |
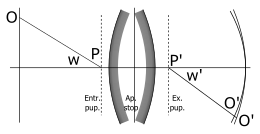 Fig. 6. |
(3) Aberration of lateral object points (points beyond the axis) with narrow pencils. Astigmatism.—A point O (fig. 6) at a finite distance from the, axis (or with an infinitely distant object, a point which subtends a finite angle at the system) is, in general, even then not sharply reproduced, if the pencil of rays issuing from it and traversing the system is made infinitely narrow by reducing the aperture stop; such a pencil consists of the rays which can pass from the object point through the now infinitely small entrance pupil. It is seen (ignoring exceptional cases) that the pencil does not meet he refracting or reflecting surface at right angles; therefore it is astigmatic (Gr. α-, privative, στίγμa, a point). Naming the central ray passing through the entrance pupil the “axis of the pencil,” or “principal ray,” we can say: the rays of the pencil intersect, not in one point, but in two focal lines, which we can assume to be at right angles to the principal ray; of these, one lies in the plane containing the principal ray and the axis of the system, i.e. in the “first principal section” or “meridional section,” and the other at right angles to it, i.e. in the second principal section or sagittal section. We receive, therefore, in no single intercepting plane behind the system, as, for example, a focussing screen, an image of the object point; on the other hand, in each of two planes lines O′ and O″ are separately formed (in neighbouring planes ellipses are formed), and in a plane between O′ and O″ a circle of least confusion. The interval O′O″, termed the astigmatic difference, increases, in general, with the angle W made by the principal ray OP with the axis of the system, i.e. with the field of view. Two “astigmatic image surfaces” correspond to one object plane; and these are in contact at the axis point; on the one lie the focal lines of the first kind, on the other those of the second. Systems in which the two astigmatic surfaces coincide are termed anastigmatic or stigmatic.
Sir Isaac Newton was probably the discoverer of astigmation; the position of the astigmatic image lines was determined by Thomas Young (A Course of Lectures on Natural Philosophy, 1807); and the theory has been recently developed by A. Gullstrand (Skand. Arch. f. physiol., 1890, 2, p. 269; Allgemeine Theorie der monochromat. Aberrationen, etc., Upsala, 1900; Arch. f. Ophth., 1901, 53, pp. 2, 185). A bibliography by P. Culmann is given in M. von Rohr’s Die Bilderzeugung in optischen Instrumenten (Berlin, 1904).
(4) Aberration of lateral object points with broad pencils. Coma.—By opening the stop wider, similar deviations arise for lateral points as have been already discussed for axial points; but in this case they are much more complicated. The course of the rays in the meridional section is no longer symmetrical to the principal ray of the pencil; and on an intercepting plane there appears, instead of a luminous point, a patch of light, not symmetrical about a point, and often exhibiting a resemblance to a comet having its tail directed towards or away from the axis. From this appearance it takes its name. The unsymmetrical form of the meridional pencil—formerly the only one considered—is coma in the narrower sense only; other errors of coma have been treated by A. König and M. von Rohr (op. cit.), and more recently by A. Gullstrand (op. cit.; Ann. d. Phys., 1905, 18, p. 941).
(5) Curvature of the field of the image.—If the above errors be eliminated, the two astigmatic surfaces united, and a sharp image obtained with a wide aperture—there remains the necessity to correct the curvature of the image surface, especially when the image is to be received upon a plane surface, e.g. in photography. In most cases the surface is concave towards the system.
(6) Distortion of the image.—If now the image be sufficiently sharp, inasmuch as the rays proceeding from every object point meet in an image point of satisfactory exactitude, it may happen that the image is distorted, i.e. not sufficiently like the object. This error consists in the different parts of the object being reproduced with different magnifications; for instance, the inner parts may differ in greater magnification than the outer (“barrel-shaped distortion”), or conversely (“cushion-shaped distortion”) (see fig. 7). 
Fig. 7.Systems free of this aberration are called “orthoscopic” (όρθός, right, σκοπεῖν to look). This aberration is quite distinct from that of the sharpness of reproduction; in unsharp, reproduction, the question of distortion arises if only parts of the object can be recognized in the figure. If, in an unsharp image, a patch of light corresponds to an object point, the “centre of gravity” of the patch may be regarded as the image point, this being the point where the plane receiving the image, e.g. a focussing screen, intersects the ray passing through the middle of the stop. This assumption is justified if a poor image on the focussing screen remains stationary when the aperture is diminished; in practice, this generally occurs. This ray, named by Abbe a “principal ray” (not to be confused with the “principal rays” of the Gaussian theory), passes through the centre of the entrance pupil before the first refraction, and the centre of the exit pupil after the last refraction. From this it follows that correctness of drawing depends solely upon the principal rays; and is independent of the sharpness or curvature of the image field.

Fig. 8.
Referring to fig. 8, we have O′Q′/OQ = a′ tan w ′/a tan w = 1/N, where N is the “scale” or magnification of the image. For N to be constant for all values of w, a′ tan w ′/a tan w must also be constant. If the ratio a′/a be sufficiently constant, as is often the case, the above relation reduces to the “condition of Airy,” i.e. tan w ′/ tan w = a constant. This simple relation (see Camb. Phil. Trans., 1830, 3, p. 1) is fulfilled in all systems which are symmetrical with respect to their diaphragm (briefly named “symmetrical or holosymmetrical objectives”), or which consist of two like, but different-sized, components, placed from the diaphragm in the ratio of their size, and presenting the same curvature to it (hemisymmetrical objectives); in these systems tan w ′/ tan w = 1. The constancy of a′/a necessary for this relation to hold was pointed out by R. H. Bow (Brit. Journ. Photog., 1861), and Thomas Sutton (Photographic Notes, 1862); it has been treated by O. Lummer and by M. von Rohr (Zeit. f. Instrumentenk., 1897, 17, and 1898, 18, p. 4). It requires the middle of the aperture stop to be reproduced in the centres of the entrance and exit pupils without spherical aberration. M. von Rohr showed that for systems fulfilling neither the Airy nor the Bow-Sutton condition, the ratio a′ tan w ′/a tan w will be constant for one distance of the object. This combined condition is exactly fulfilled by holosymmetrical objectives reproducing with the scale 1, and by hemisymmetrical, if the scale of reproduction be equal to the ratio of the sizes of the two components.
Analytic Treatment of Aberrations.—The preceding review of the several errors of reproduction belongs to the “Abbe theory of aberrations,” in which definite aberrations are discussed separately; it is well suited to practical needs, for in the construction of an optical instrument certain errors are sought to be eliminated, the selection of which is justified by experience. In the mathematical sense, however, this selection is arbitrary; the reproduction of a finite object with a finite aperture entails, in all probability, an infinite number of aberrations. This number is only finite if the object and aperture are assumed to be “infinitely small of a certain order”; and with each order of infinite smallness, i.e. with each degree of approximation to reality (to finite objects and apertures), a certain number of aberrations is associated. This connexion is only supplied by theories which treat aberrations generally and analytically by means of indefinite series.
 Fig. 9. |
The nature of the reproduction consists in the rays proceeding from a point O being united in another point O′; in general, this will not be the case, for ξ′, η′ vary if ξ, η be constant, but x, y variable. It may be assumed that the planes I′ and II′ are drawn where the images of the planes I and II are formed by rays near the axis by the ordinary Gaussian rules; and by an extension of these rules, not, however, corresponding to reality, the Gauss image point O′0, with co-ordinates ξ′0,η′0, of the point O at some distance from the axis could be constructed. Writing Δξ′=ξ−ξ′0 and Δη′=η′−η′0, then Δξ′ and Δη′ are the aberrations belonging to ξ, η and x, y, and are functions of these magnitudes which, when expanded in series, contain only odd powers, for the same reasons as given above. On account of the aberrations of all rays which pass through O, a patch of light, depending in size on the lowest powers of ξ, η and x, y which the aberrations contain, will be formed in the plane I′. These degrees, named by J. Petzval (Bericht über die Ergebnisse einiger dioptrischer Untersuchungen, Buda Pesth, 1843; Akad. Sitzber., Wien, 1857, vols. xxiv. xxvi.) “the numerical orders of the image,” are consequently only odd powers; the condition for the formation of an image of the mth order is that in the series for Δξ′ and Δη′ the coefficients of the powers of the 3rd, 5th . . . (m−2)th degrees must vanish. The images of the Gauss theory being of the third order, the next problem is to obtain an image of 5th order, or to make the coefficients of the powers of 3rd degree zero. This necessitates the satisfying of five equations; in other words, there are five alterations of the 3rd order, the vanishing of which produces an image of the 5th order.
The expression for these coefficients in terms of the constants of the optical system, i.e. the radii, thicknesses, refractive indices and distances between the lenses, was solved by L. Seidel (Astr. Nach., 1856, p. 1289); in 1840, J. Petzval constructed his portrait objective, unexcelled even at the present day, from similar calculations, which have never been published (see M. von Rohr, Theorie und Geschichte des photographischen Objectivs, Berlin, 1899, p. 248). The theory was elaborated by S. Finterswalder (München. Akad. Abhandl., 1891, 17, p. 519), who also published a posthumous paper of Seidel containing a short view of his work (München. Akad. Sitzber., 1898, 28, p. 395); a simpler form was given by A. Kerber (Beiträge zur Dioptrik, Leipzig, 1895–6–7–8–9). A. König and M. von Rohr (see M. von Rohr, Die Bilderzeugung in optischen Instrumenten, pp. 317-323) have represented Kerber’s method, and have deduced the Seidel formulae from geometrical considerations based on the Abbe method, and have interpreted the analytical results geometrically (pp. 212-316).
The aberrations can also be expressed by means of the “characteristic function” of the system and its differential coefficients, instead of by the radii, &c., of the lenses; these formulae are not immediately applicable, but give, however, the relation between the number of aberrations and the order. Sir William Rowan Hamilton (British Assoc. Report, 1833, p. 360) thus derived the aberrations of the third order; and in later times the method was pursued by Clerk Maxwell (Proc. London Math. Soc., 1874–1875; see also the treatises of R. S. Heath and L. A. Herman), M. Thiesen (Berlin. Akad. Sitzber., 1890, 35, p. 804), H. Bruns (Leipzig. Math. Phys. Ber., 1895, 21, p. 410), and particularly successfully by K. Schwartzschild (Göttingen. Akad. Abhandl., 1905, 4, No. 1), who thus discovered the aberrations of the 5th order (of which there are nine), and possibly the shortest proof of the practical (Seidel) formulae. A. Gullstrand (vide supra, and Ann. d. Phys., 1905, 18, p. 941) founded his theory of aberrations on the differential geometry of surfaces.
The aberrations of the third order are: (1) aberration of the axis point; (2) aberration of points whose distance from the axis is very small, less than of the third order—the deviation from the sine condition and coma here fall together in one class; (3) astigmatism; (4) Aberrations of the third order.curvature of the field; (5) distortion.
(1) Aberration of the third order of axis points is dealt with in all text-books on optics. It is important for telescope objectives, since their apertures are so small as to permit higher orders to be neglected. For a single lens of very small thickness and given power, the aberration depends upon the ratio of the radii r : r ′, and is a minimum (but never zero) for a certain value of this ratio; it varies inversely with the refractive index (the power of the lens remaining constant). The total aberration of two or more very thin lenses in contact, being the sum of the individual aberrations, can be zero. This is also possible if the lenses have the same algebraic sign. Of thin positive lenses with n=1·5, four are necessary to correct spherical aberration of the third order. These systems, however, are not of great practical importance. In most cases, two thin lenses are combined, one of which has just so strong a positive aberration (“under-correction,” vide supra) as the other a negative; the first must be a positive lens and the second a negative lens; the powers, however, may differ, so that the desired effect of the lens is maintained. It is generally an advantage to secure a great refractive effect by several weaker than by one high-power lens. By one, and likewise by several, and even by an infinite number of thin lenses in contact, no more than two axis points can be reproduced without aberration of the third order. Freedom from aberration for two axis points, one of which is infinitely distant, is known as “Herschel’s condition.” All these rules are valid inasmuch as the thicknesses and distances of the lenses are not to be taken into account.
(2) The condition for freedom from coma in the third order is also of importance for telescope objectives; it is known as “Fraunhofer’s condition.” (4) After eliminating the aberration on the axis, coma and astigmatism, the relation for the flatness of the field in the third order is expressed by the “Petzval equation,” Σ1/r (n′−n)=0, where r is the radius of a refracting surface, n and n′ the refractive indices of the neighbouring media, and Σ the sign of summation for all refracting surfaces.
Practical Elimination of Aberrations.—The existence of an optical system, which reproduces absolutely a finite plane on another with pencils of finite aperture, is doubtful; but practical systems solve this problem with an accuracy which mostly suffices for the special purpose of each species of instrument. The problem of finding a system which reproduces a given object upon a given plane with given magnification (in so far as aberrations must be taken into account) could be dealt with by means of the approximation theory; in most cases, however, the analytical difficulties are too great. Solutions, however, have been obtained in special cases (see A. König in M. von Rohr’s Die Bilderzeugung, p. 373; K. Schwarzschild, Göttingen. Akad. Abhandl., 1905, 4, Nos. 2 and 3). At the present time constructors almost always employ the inverse method: they compose a system from certain, often quite personal experiences, and test, by the trigonometrical calculation of the paths of several rays, whether the system gives the desired reproduction (examples are given in A. Gleichen, Lehrbuch der geometrischen Optik, Leipzig and Berlin, 1902). The radii, thicknesses and distances are continually altered until the errors of the image become sufficiently small. By this method only certain errors of reproduction are investigated, especially individual members, or all, of those named above. The analytical approximation theory is often employed provisionally, since its accuracy does not generally suffice.
In order to render spherical aberration and the deviation from the sine condition small throughout the whole aperture, there is given to a ray with a finite angle of aperture u* (with infinitely distant objects: with a finite height of incidence h*) the same distance of intersection, and the same sine ratio as to one neighbouring the axis (u* or h* may not be much smaller than the largest aperture U or H to be used in the system). The rays with an angle of aperture smaller than u* would not have the same distance of intersection and the same sine ratio; these deviations are called "zones, " and the constructor endeavours to reduce these to a minimum. The same holds for the errors depending upon the angle of the field of view, w: astigmatism, curvature of field and distortion are eliminated for a definite value, w*; “zones of astigmatism, curvature of field and distortion” attend smaller values of w. The practical optician names such systems: “corrected for the angle of aperture u* (the height of incidence h*), or the angle of field of view w*.” Spherical aberration and changes of the sine ratios are often represented graphically as functions of the aperture, in the same way as the deviations of two astigmatic image surfaces of the image plane of the axis point are represented as functions of the angles of the field of view.
The final form of a practical system consequently rests on compromise; enlargement of the aperture results in a diminution of the available field of view, and vice versa. The following may be regarded as typical:—(1) Largest aperture; necessary corrections are—for the axis point, and sine condition; errors of the field of view are almost disregarded; example—high power microscope objectives. (2) Largest field of view; necessary corrections are—for astigmatism, curvature of field and distortion; errors of the aperture only slightly regarded; examples—photographic widest angle objectives and oculars. Between these extreme examples stands the ordinary photographic objective: the portrait objective is corrected more with regard to aperture; objectives for groups more with regard to the field of view. (3) Telescope objectives have usually not very large apertures, and small fields of view; they should, however, possess zones as small as possible, and be built in the simplest manner. They are the best for analytical computation.
(b) Chromatic or Colour Aberration.
In optical systems composed of lenses, the position, magnitude and errors of the image depend upon the refractive indices of the glass employed (see Lens, and above, “Monochromatic Aberration”). Since the index of refraction varies with the colour or wave length of the light (see Dispersion), it follows that a system of lenses (uncorrected) projects images of different colours in somewhat different places and sizes and with different aberrations; i.e. there are “chromatic differences” of the distances of intersection, of magnifications, and of monochromatic aberrations. If mixed light be employed (e.g. white light) all these images are formed; and since they are all ultimately intercepted by a plane (the retina of the eye, a focussing screen of a camera, &c.), they cause a confusion, named chromatic aberration; for instance, instead of a white margin on a dark background, there is perceived a coloured margin, or narrow spectrum. The absence of this error is termed achromatism, and an optical system so corrected is termed achromatic. A system is said to be “chromatically under-corrected” when it shows the same kind of chromatic error as a thin positive lens, otherwise it is said to be “over-corrected.”
If, in the first place, monochromatic aberrations be neglected —in other words, the Gaussian theory be accepted—then every reproduction is determined by the positions of the focal planes, and the magnitude of the focal lengths, or if the focal lengths, as ordinarily happens, be equal, by three constants of reproduction. These constants are determined by the data of the system (radii, thicknesses, distances, indices, &c., of the lenses); therefore their dependence on the refractive index, and consequently on the colour, are calculable (the formulae are given in Czapski-Eppenstein, Grundzüge der Theorie der optischten Instrumente (1903, p. 166). The refractive indices for different wave lengths must be known for each kind of glass made use of. In this manner the conditions are maintained that any one constant of reproduction is equal for two different colours, i.e. this constant is achromatized. For example, it is possible, with one thick lens in air to achromatize the position of a focal plane of the magnitude of the focal length. If all three constants of reproduction be achromatized, then the Gaussian image for all distances of objects is the same for the two colours, and the system is said to be in “stable achromatism.”
In practice it is more advantageous (after Abbe) to determine the chromatic aberration (for instance, that of the distance of intersection) for a fixed position of the object, and express it by a sum in which each component contains the amount due to each refracting surface (see Czapski-Eppenstein, op. cit. p. 170; A. König in M. v. Rohr’s collection, Die Bilderzeugung, p. 340). In a plane containing the image point of one colour, another colour produces a disk of confusion; this is similar to the confusion caused by two “zones” in spherical aberration. For infinitely distant objects the radius of the chromatic disk of confusion is proportional to the linear aperture, and independent of the focal length (vide supra, “Monochromatic Aberration of the Axis Point”); and since this disk becomes the less harmful with an increasing image of a given object, or with increasing focal length, it follows that the deterioration of the image is proportional to the ratio of the aperture to the focal length, i.e. the relative aperture.” (This explains the gigantic focal lengths in vogue before the discovery of achromatism.)
Examples.—(a) In a very thin lens, in air, only one constant of reproduction is to be observed, since the focal length and the distance of the focal point are equal. If the refractive index for one colour be n, and for another n+dn, and the powers, or reciprocals of the focal lengths, be φ and φ+dφ, then (1) dφ/φ=dn/(n−1)=1/ν; dn is called the dispersion, and ν the dispersive power of the glass.
(b) Two thin lenses in contact: let φ1 and φ2 be the powers corresponding to the lenses of refractive indices n1 and n2 and radii r ′1, r ′′1, and r ′2, r ′′2 respectively; let φ denote the total power, and dφ, dn1, d2 the changes of φ, n1, and n2 with the colour. Then the following relations hold:
(2) φ=φ1+φ2 = (n1 − 1)(1/r1 − 1/r ′′1)+(n2 − 1)(1/r ′2 − 1/r ′′2) = (n1 − 1)k1+(n2 − 1)k2; and
(3) dφ = k1dn1 + k2dn2. For achromatism dφ = 0, hence, from (3),
(4) k1/k2 = −dn2/dn1, or φ1/φ2 = −ν1/ν2. Therefore φ1 and φ2 must have different algebraic signs, or the system must be composed of a collective and a dispersive lens. Consequently the powers of the two must be different (in order that φ be not zero (equation 2)), and the dispersive powers must also be different (according to 4).
Newton failed to perceive the existence of media of different dispersive powers required by achromatism; consequently he constructed large reflectors instead of refractors. James Gregory and Leonhard Euler arrived at the correct view from a false conception of the achromatism of the eye; this was determined by Chester More Hall in 1728, Klingenstierna in 1754 and by Dollond in 1757, who constructed the celebrated achromatic telescopes. (See Telescope.)
Glass with weaker dispersive power (greater ν) is named “crown glass”; that with greater dispersive power, “flint glass.” For the construction of an achromatic collective lens (φ positive) it follows, by means of equation (4), that a collective lens I. of crown glass and a dispersive lens II. of flint glass must be chosen; the latter, although the weaker, corrects the other chromatically by its greater dispersive power. For an achromatic dispersive lens the converse must be adopted.
This is, at the present day, the ordinary type, e.g., of telescope objective (fig. 10); the values of the four radii must satisfy the equations (2) and (4). Two other conditions may also be postulated; one is always the elimination of the aberration on the axis; the second either the Herschel” or “Fraunhofer condition,” the latter being the best (vide supra, “Monochromatic Aberation”). In practice, however, it is often more useful to avoid the second condition by making, the lenses have contact, i.e. equal radii. According to P. Rudolph (Eder’s Jahrb. f. Photog., 1891, 5, p. 225; 1893, 7, p. 221), cemented objectives of thin lenses permit the elimination of spherical aberration on the axis, if, as above, the collective lens has a smaller refractive index; on the other hand, they permit the elimination of astigmatism and curvature of the field, if the collective lens has a greater refractive index (this follows from the Petzval equation; see L. Seidel, Astr. Nachr., 1856, p. 289). Should the cemented system be positive, then the more powerful lens must be positive; and, according to (4), to the greater power belongs the weaker dispersive power (greater ν), that is to say, crown glass; consequently the crown glass must have the greater refractive index for astigmatic and plane images. In all earlier kinds of glass, however, the dispersive power increased with the refractive index; that is, ν decreased as n increased; but some of the Jena glasses by E. Abbe and O. Schott were crown glasses of high refractive index, and achromatic systems from such crown glasses, with flint glasses of lower refractive index, are called the “new achromats,” and were employed by P. Rudolph in the first “anastigmats” (photographic objectives).
Instead of making dφ vanish, a certain value can be assigned to it which will produce, by the addition of the two lenses, any desired chromatic deviation, e.g. sufficient to eliminate one present in other parts of the system. If the lenses I. and II. be cemented and have the same refractive index for one colour, then its effect for that one colour is that of a lens of one piece; by such decomposition of a lens it can be made chromatic or achromatic at will, without altering its spherical effect. If its chromatic effect (dφ/φ) be greater than that of the same lens, this being made of the more dispersive of the two glasses employed, it is termed “hyper-chromatic.”
For two thin lenses separated by a distance D the condition for achromatism is D=(v1f1+v2f2) (v1+v2); if v1=v2 (e.g. if the lenses be made of the same glass), this reduces to D=12 (f1+f2), known as the “condition for oculars.”
If a constant of reproduction, for instance the focal length, be made equal for two colours, then it is not the same for other colours, if two different glasses are employed. For example, the condition for achromatism (4) for two thin lenses in contact is fulfilled in only one part of the spectrum, since dn2/dn1 varies within the spectrum. This fact was first ascertained by J. Fraunhofer, who defined the colours by means of the dark lines in the solar spectrum; and showed that the ratio of the dispersion of two glasses varied about 20% from the red to the violet (the variation for glass and water is about 50%). If, therefore, for two colours, a and b, fa=fb=f, then for a third colour, c, the focal length is different, viz. if c lie between a and b, then fc <f, and vice versa; these algebraic results follow from the fact that towards the red the dispersion of the positive crown glass preponderates, towards the violet that of the negative flint. These chromatic errors of systems, which are achromatic for two colours, are called the “secondary spectrum,” and depend upon the aperture and focal length in the same manner as the primary chromatic errors do.
In fig. 11, taken from M. von Rohr’s Theorie und Geschichte des photographischen Objectivs, the abscissae are focal lengths, and the ordinates wave-lengths; of the latter the Fraunhofer lines used are—
| A′ | C | D | Green Hg. | F | G′ | Violet Hg. |
| 767·7 | 656·3 | 589·3 | 546·1 | 486·2 | 454·1 | 405·1 μμ, |

Fig. 11.—Secondary Spectrum of the combination O. 1726, O. 108. Optical correction fc=ff=100mm. The ordinates give the wave-length in μμ. The abscissae give fλ - fc in 0·01mm., commencing at fc ff.
(From M. v. Rohr, op. cit.)
and the focal lengths are made equal for the lines C and F. In the neighbourhood of 550 μμ the tangent to the curve is parallel to the axis of wave-lengths; and the focal length varies least over a fairly large range of colour, therefore in this neighbourhood the colour union is at its best. Moreover, this region of the spectrum is that which appears brightest to the human eye, and consequently this curve of the secondary spectrum, obtained by making fc=ff, is, according to the experiments of Sir G. G. Stokes (Proc. Roy. Soc., 1878), the most suitable for visual instruments (“optical achromatism”). In a similar manner, for systems used in photography, the vertex of the colour curve must be placed in the position of the maximum sensibility of the plates; this is generally supposed to be at G′; and to accomplish this the F and violet mercury lines are united. This artifice is specially adopted in objectives for astronomical photography (“pure actinic achromatism”). For ordinary photography, however, there is this disadvantage: the image on the focussing-screen and the correct adjustment of the photographic sensitive plate are not in register; in astronomical photography this difference is constant, but in other kinds it depends on the distance of the objects. On this account the lines D and G′ are united for ordinary photographic objectives; the optical as well as the actinic image is chromatically inferior, but both lie in the same place; and consequently the best correction lies in F (this is known as the “actinic correction” or “freedom from chemical focus”).
Should there be in two lenses in contact the same focal lengths for three colours a, b, and c, i.e. fa=fb=fc=f, then the relative partial dispersion (nc−nb) (na−nb) must be equal for the two kinds of glass employed. This follows by considering equation (4) for the two pairs of colours ac and bc. Until recently no glasses were known with a proportional degree of absorption; but R. Blair (Trans. Edin. Soc., 1791, 3, p. 3), P. Barlow, and F. S. Archer overcame the difficulty by constructing fluid lenses between glass walls. Fraunhofer prepared glasses which reduced the secondary spectrum; but permanent success was only assured on the introduction of the Jena glasses by E. Abbe and O. Schott. In using glasses not having proportional dispersion, the deviation of a third colour can be eliminated by two lenses, if an interval be allowed between them; or by three lenses in contact, which may not all consist of the old glasses. In uniting three colours an “achromatism of a higher order” is derived; there is yet a residual “tertiary spectrum,” but it can always be neglected.
The Gaussian theory is only an approximation; monochromatic or spherical aberrations still occur, which will be different for different colours; and should they be compensated for one colour, the image of another colour would prove disturbing. The most important is the chromatic difference of aberration of the axis point, which is still present to disturb the image, after par-axial rays of different colours are united by an appropriate combination of glasses. If a collective system be corrected for the axis point for a definite wave-length, then, on account of the greater dispersion in the negative components—the flint glasses,—over-correction will arise for the shorter wavelengths (this being the error of the negative components), and under-correction for the longer wave-lengths (the error of crown glass lenses preponderating in the red). This error was treated by Jean le Rond d’Alembert, and, in special detail, by C. F. Gauss. It increases rapidly with the aperture, and is more important with medium apertures than the secondary spectrum of par-axial rays; consequently, spherical aberration must be eliminated for two colours, and if this be impossible, then it must be eliminated for those particular wave-lengths which are most effectual for the instrument in question (a graphical representation of this error is given in M. von Rohr, Theorie und Geschichte des photographischen Objectivs).
The condition for the reproduction of a surface element in the place of a sharply reproduced point—the constant of the sine relation—must also be fulfilled with large apertures for several colours. E. Abbe succeeded in computing microscope objectives free from error of the axis point and satisfying the sine condition for several colours, which therefore, according to his definition, were “aplanatic for several colours”; such systems he termed “apochromatic”. While, however, the magnification of the individual zones is the same, it is not the same for red as for blue; and there is a chromatic difference of magnification. This is produced in the same amount, but in the opposite sense, by the oculars, which are used with these objectives (“compensating oculars”), so that it is eliminated in the image of the whole microscope. The best telescope objectives, and photographic objectives intended for three-colour work, are also apochromatic, even if they do not possess quite the same quality of correction as microscope objectives do. The chromatic differences of other errors of reproduction have seldom practical importances.
Authorities.—The standard treatise in English is H. D. Taylor, A System of Applied Optics (1906); reference may also be made to R. S. Heath, A Treatise on Geometrical Optics (2nd ed., 1895); and L. A. Herman, A Treatise on Geometrical Optics (1900). The ideas of Abbe were first dealt with in S. Czapski, Theorie der optischen Instrumente nach Abbe, published separately at Breslau in 1893, and as vol. ii. of Winkelmann’s Handbuch der Physik in 1894; a second edition, by Czapski and O. Eppenstein, was published at Leipzig in 1903 with the title, Grundzüge der Theorie der optischen Instrumente nach Abbe, and in vol. ii. of the 2nd ed. of Winkelmann’s Handbuch der Physik. The collection of the scientific staff of Carl Zeiss at Jena, edited by M. von Rohr, Die bilderzeugung in optischen Instrumenten vom Standpunkte der geometrischen Optik (Berlin, 1904), contains articles by A. König and M. von Rohr specially dealing with aberrations. (O. E.)
- ↑ The investigations of E. Abbe on geometrical optics, originally published only in his university lectures, were first compiled by S. Czapski in 1893. See below, Authorities.
